Задачи, описывающие смешивание веществ

Основными компонентами задач, описывающих смешивание, являются массы или объемы смешиваемых веществ, а также концентрация или процентное содержание одного или нескольких веществ в смеси. Если М единиц смеси содержит m единиц какого-либо вещества, то концентрация этого вещества в смеси (количество вещества в единице объема или массы) составляет 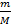, а процентное содержание вещества представляет собой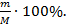

При смешивании двух или нескольких растворов или сплавов общая масса (объем) равна сумме масс (объемов) смешиваемых компонентов.

Если в задаче фигурирует несколько растворов или раствор (смесь) меняется по составу на протяжении задачи, то удобно составить таблицу, в которой отражены описание смеси, масса или объем смеси, доля конкретного вещества в смеси, его масса или объем. По мере решения задачи строки в таблице будут заполняться.

Задача 1. Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45 % меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы получившийся новый сплав содержал 40 % меди?

Решение. 45 % составляет 0,45 всего сплава, поэтому в сплаве содержится меди 0,45∙12=5,4 кг, а олова (12 – 5,4) = 6,6 кг. В новом сплаве медь будет составлять 40 %, а олово – 60 %. Составим пропорцию:

.

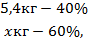
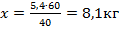В новом сплаве олова 8,1 кг, следовательно, добавка олова составила (8,1 – 6,6) = 1,5 кг.

Ответ: к сплаву надо прибавить 1,5 кг олова.

Замечание. Задачу можно было решить, составив таблицу и приняв количество добавляемого олова за х.

Таблица1

Описание смеси. Количество добавляемого чистого олова.

Описание смеси	Масса смеси, кг	Доля меди, %	Доля олова, %	Масса меди, кг	Масса олова, кг
1-й сплав: медь и олово				12·0,45 = 5,4	12·0,55 = 6,6
2-й сплав: медь и олово	12 + х			5,4	6,6 + х

Поскольку олово составляет в новом сплаве 60 %, то можно записать соотношение 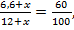откуда 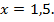Таким образом, к сплаву надо добавить 1,5 кг олова.

Задача 2. Из сосуда, наполненного кислотой, вылили несколько литров и долили водой; потом опять вылили столько же литров смеси, тогда в сосуде осталось 24 л чистой кислоты. Емкость сосуда 54 л. Сколько кислоты вылили в первый и второй раз?

Решение. Первоначально сосуд содержал 54 л кислоты. Пусть в первый раз из сосуда вылили х литров кислоты, тогда в нем осталось (54 – х) литров кислоты и добавилось х литров воды, которую долили в сосуд. В сосуде вновь стало 54 л жидкости, каждый литр которой содержал 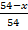литров кислоты и 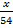литров воды. Затем из сосуда вылили х литров смеси, в которой содержалось 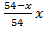литров кислоты.

В сосуде осталось 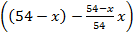литров кислоты, что составило 24 л.

Найдем из этого соотношения х: _;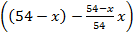

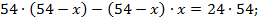
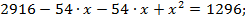
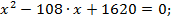
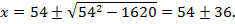
По условию задачи 0< x <54, поэтому х =90является посторонним корнем. Из сосуда в первый раз вылили х = 18 л кислоты, во второй раз вылили 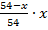л, т. е. 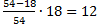л.

Ответ: из сосуда вылили 18 л кислоты в первый раз и 12 л кислоты во второй раз.

Замечание. В этой задаче также удобно составить таблицу, в которой подробно можно проследить все изменения смеси.

Таблица 2

Описание смеси. Изменение смеси сплава.

Описание смеси	Объем смеси, л	Доля кислоты, %	Объем кислоты, л	Объем воды, л
1-я смесь: кислота
2-я смесь: кислота с водой		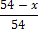		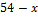х
3-я смесь: кислота с водой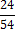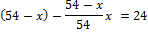

Уравнение, которое приводит к окончательному результату, получилось внутри таблицы в третьей строке. Теперь осталось его решить и записать ответ, что уже было проделано ранее.

Задачи на проценты

Задачи на проценты в последнее время довольно часто встречаются как в вариантах Единого государственного экзамена, так и в вариантах вступительных экзаменов в вузы. Это связано с тем, что подобного рода вопросы нередко приходится решать и в повседневной жизни (банковские проценты, ставки по кредитам и многое другое). Некоторые задачи на смешивание вещества также можно отнести к задачам на проценты. Интерес представляют задачи на банковские проценты, а также задачи, в которых сравниваются некоторые величины в их процентном соотношении. Определенные опасения, с которыми учащиеся приступают к решению подобного рода задач, не имеют под собой реальной почвы. Надо хорошо представлять, что один процент – это просто одна сотая часть от общего объема и не более того.

Задача 1. По сберегательному вкладу банк выплачивает 12 % годовых. По истечении каждого года начисленная сумма присоединяется к вкладу. На этот вид вклада был открыт счет в 10000 рублей, который не пополнялся и с которого не снимались деньги в течение двух лет. Какой доход был получен по истечении этого срока?

Решение. Рассмотрим предварительно общий подход к задачам подобного вида. Пусть х рублей – первоначальный взнос, р – проценты, которые банк ежегодно добавляет к сумме вклада. Таким образом, вклад ежегодно увеличивается на 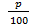часть от имеющейся на начало года суммы. Следовательно, через год сумма вклада увеличится на 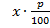рублей и будет составлять 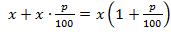рублей. Через два года вклад окажется равным:

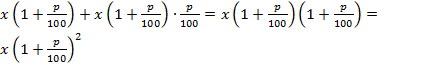рублям.

Рассуждая далее аналогичным образом, получим формулу, по которой можно вычислить сумму вклада Х через n лет: 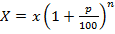рублей.

Теперь перейдем непосредственно к сформулированной выше задаче. Первоначальный вклад х = 10000 рублей, процентная ставка р = 12 %, или 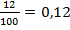от первоначальной суммы. Тогда через два года сумма вклада составит:

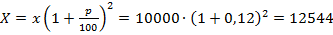рубля, а доход будет равен разности между этой суммой и первоначальным взносом: 12544 – 10000 = 2544 рубля.

Ответ: по истечении срока будет получен доход в размере 2544 рублей.

Задача 2. Количество студентов в институте ежегодно увеличивалось на один и тот же процент и за три года возросло от 1000 до 1728 человек. На сколько процентов увеличивалось число студентов ежегодно?

Решение. Нетрудно догадаться, что эта задача аналогична предыдущей. Пусть ежегодный прирост студентов составляет р процентов, х = 1000 – первоначальное количество студентов, Х = 1728 – число обучающихся через три года, поэтому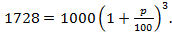

Решим это уравнение:

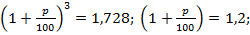р = 20 %.

Ответ: число студентов ежегодно увеличивалось на 20 %.

Задача 3. Найти два числа, если 10 % первого числа составляют 25 % от второго, а отношение произведения этих чисел к их сумме равно 10.

Решение. Обозначим первое число за х, а второе – за у. Тогда, согласно условию задач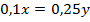и, и 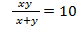. Запишем уравнения в систему и решим ее:

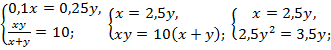
из второго уравнения у = 0 или у = 14. Если у = 0, то и х = 0, что противоречит второму уравнению системы, поэтому у = 14, а х = 35.

Ответ: искомые числа 35 и 14.

Задача 4. Рабочий день уменьшился от 8 до 7 ч. На сколько процентов нужно повысить производительность труда, чтобы при тех же расценках заработная плата выросла на 5 %?

Решение. Предположим, что первоначально производительность труда на предприятии составляла х единиц продукции в час, тогда за восьмичасовую рабочую смену изготовлялось 8х единиц продукции. Если повысить производительность труда на р процентов, то за час будет изготовлено 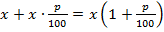единиц продукции, а за семичасовой рабочий день 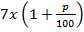единиц продукции, что составляет 105 % от 8х.

Составим соотношение 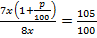, откуда р = 20 %.

Ответ: производительность труда нужно повысить на 20 %.

Замечание. Если в задачах производится сравнение в процентном соотношении, то за 100 % следует принимать величину, с которой производится сравнение.

Задача 5.Свежие фрукты содержат 72 % воды, а сухие – 20 % воды. Сколько сухих фруктов получится из 20 кг свежих?

Решение. При решении подобных задач следует определить ту величину, которая не меняется при высыхании (уменьшении влажности). Неизменной в данных процессах остается масса сухого вещества, т. е. продукта, в котором полностью отсутствует вода. Если 20 кг фруктов имеют влажность 72 %, то жидкость составляет 20∙ 0,72 = 14,4 кг, а сухое вещество имеет массу 20 – 14,4 = 5,6 кг. Масса сухого вещества не меняется при высыхании, поэтому в сухих фруктах, содержащих 20 % воды, сухое вещество составляет 80 %. Следовательно, 5,6 кг являются 0,8 частью от общей массы сухих фруктов, а вся масса равняется 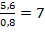кг.

Можно было получить результат, составив пропорцию

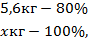
откуда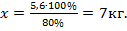

Ответ: из 20 кг свежих фруктов получится 7 кг сухих.

Задача 6. Себестоимость продукции повысилась сначала на 10 %, а затем понизилась на 20 %. На сколько процентов понизилась себестоимость продукции по сравнению с первоначальной?

Решение. Пусть первоначальная себестоимость продукции составляла х рублей, тогда повышение на 10 % привело к себестоимости продукции х + 0,1 ∙ х = 1,1х рублей. Понизив указанную себестоимость на 20 %, получим 1,1х – 1,1х ∙ 0,2 = 0,88х рублей. Разность между первоначальной себестоимостью и полученной составила х – 0,88х = 0,12х рублей или, в процентном соотношении,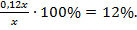

Ответ: себестоимость продукции понизилась на 12 %.

Задача 7. Число а составляет 92 % от числа b. Если b увеличить на 700, то новое число будет на 9 % больше числа а. Найти числа а и b.

Решение. Как обычно за 100 % принимаем то число, с которым производится сравнение, в данном случае – число b. Тогда а = 0,92b. Увеличив числоb на 700, получим (b + 700), что составляет 1,09 от числа а, т. е. (b + 700) = 1,09а.

Запишем систему и решим ее:

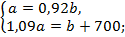
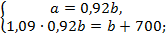
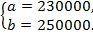
Ответ: а = 230000, b = 250000.