Изгиб. Определение напряжений в поперечных сечениях

Изгибомназывается такой вид деформации балки, который сопровождается искривлением ее оси (рис. 9.5а) либо изменением ее начальной кривизны (рис. 9.5б).

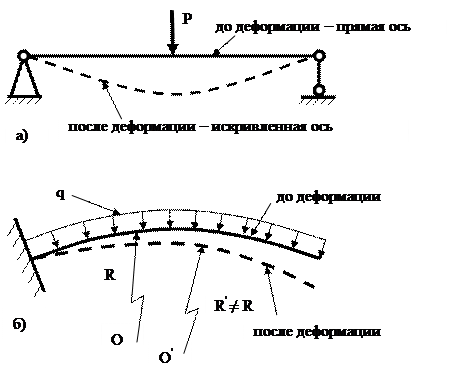
Рис. 9.5 Деформация изгиба

Изгиб прямого бруса может быть вызван поперечными внешними силами и при некоторых условиях — продольными. Отсюда изгиб, вызванный поперечной нагрузкой, называется поперечным (рис. 9.6а), а изгиб, вызванный продольными силами, называется продольным (рис. 9.6б).

Поперечный изгиб подразделяется на прямой (плоский) и косой. Если силовая плоскость (плоскость действия внешних сил) совпадает с одной из главных плоскостей инерции сечения балки, то изгиб называется прямым. В случае, когда это условие не выполняется, но силовая плоскость проходит через центр тяжести сечений, изгиб называется косым.

В настоящей теме рассматривается плоский изгиб прямых балок и составленных из них конструкций под действием внешних нагрузок. В общем случае в поперечном сечении балки действуют изгибающий момент M_x и поперечная сила Q_y (тогда изгиб называют поперечным) или только изгибающий момент M_x (тогда изгиб называют чистым).

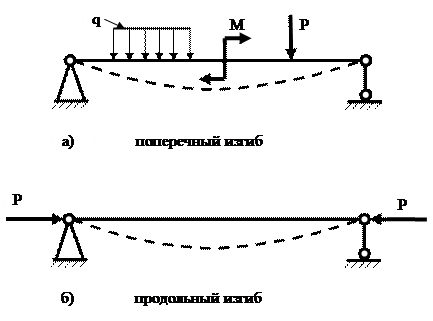
Рис.9.6 Поперечный и продольный изгиб

Таким образом, при чистом изгибе в поперечных сечениях балки действует лишь один внутренний силовой фактор – изгибающий момент, при этом в точках сечения возникают только нормальные напряжения σ. Ранее получены дифференциальные зависимости между изгибающим моментом и поперечной силой dM/dz = Q, а так как Q = 0, то изгибающий момент по длине балки постоянен.

Получим формулу для определения нормальных напряжений при чистом изгибе. Экспериментальные исследования деформации балок при чистом изгибе позволили выявить следующие закономерности:

1. Сечения, перпендикулярные к оси балки до нагружения, остаются плоскими и перпендикулярными к ее оси и после нагружения, а ось балки принимает форму дуги окружности радиуса R (рис. 9.5);

2. Деформации возникают вследствие поворота поперечных сечений друг относительно друга, при этом одни волокна балки удлиняются, а другие – сжимаются. Переход от растянутых волокон к сжатым осуществляется плавно, так что существует слой, длина которого не изменяется. Этот слой называется нейтральным. Нейтральный слой пересекается с поперечным сечением по нейтральной линии, причем данная линия перпендикулярна к плоскости кривизны изогнутой балки.

Выделим из стержня произвольного поперечного сечения элемент длиной dz (рис. 9.7а) и изобразим его в деформированном состоянии (рис. 9.7б), учитывая ранее принятые закономерности.

Нейтральные слои при изгибе не изменяют свою длину, а значит и после деформации длина нейтрального слоя равна dz. Обозначим радиус кривизны нейтрального слоя после деформации ρ и определим линейную деформацию слоя АВ (длина после деформации А₁В₁), расположенного на расстоянии yот нейтрального слоя

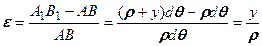. (9.12)

В формуле (9.12) учтено, что АВ = dz = ρdθ.

По закону Гука при растяжении сжатии (в данном случае волокон) напряжения будут равны

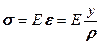. (9.13)

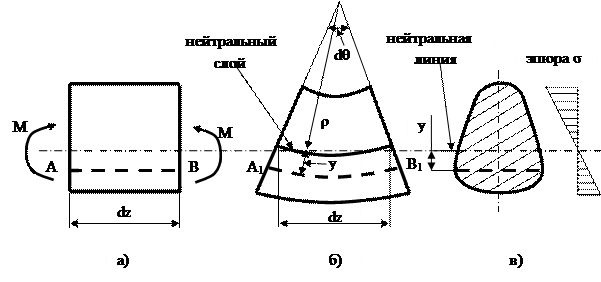
Рис. 9.7. Определение напряжений при чистом изгибе

Из зависимости (9.13) следует, что нормальные напряжения по высоте сечения изменяются по линейному закону пропорционально расстоянию от нейтральной линии (рис. 9.7в).

Выразим внутренние силовые факторы через напряжения, учитывая, что в сечениях балки действует только изгибающий момент М_x, а остальные внутренние силовые факторы равны нулю (чистый изгиб). Свяжем с балкой систему координат Oxyz, причем ось Oz направим вдоль ось стержня, а ось Ox по нейтральной линии, как показано на рис. 9.8.

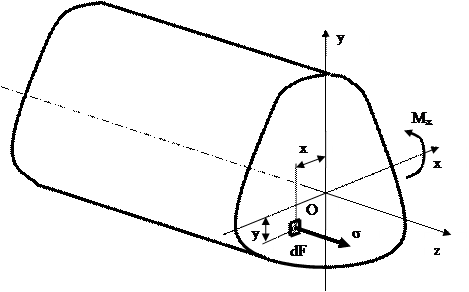
Рис. 9.8. Вычисление изгибающего момента в сечении балки

Предположим, что нормальные напряжения σ, действующие на произвольной элементарной площадке dF с координатами x и y известны. Тогда нормальная силы в данном сечении равна нулю, т.е.

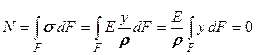. (9.14)

Откуда .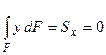

Таким образом, статический момент относительно оси Ox, совпадающей с нейтральной линией, равен нулю, а сама нейтральная линия проходит через центр тяжести сечения (ось Ox - центральная). В принятой системе координат изгибающий момент М_y равен нулю, следовательно,

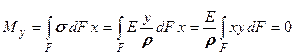. (9.15)

Откуда .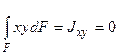

Если центробежный момент инерции равен нулю, то (см. п.9.1) оси выбранной системы координат будут не только центральными, но и главными, а значит, осевые моменты инерции принимают экстремальные значения.

Выразим значение изгибающего момента M_x через нормальные напряжения:

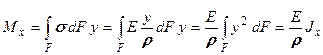. (9.16)

Из выражения (9.16) находим радиус кривизны оси балки при чистом изгибе

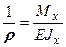. (9.17)

Подставляя (9.17) в (9.13), получим

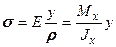. (9.18)

Анализ формулы (9.18) показывает, что максимальные напряжения при чистом изгибе возникают в точках, максимально удаленных от нейтральной линии. Эти напряжения вычисляют по формуле

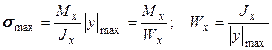, (9.19)

где W_x – момент сопротивления сечения при изгибе, который для наиболее распространенных сечений приводится в справочной литературе. Так, для балки прямоугольного сечения при изгибе относительно центральной оси, параллельной меньшей стороне b имеем:

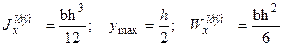. (9.20)

Для балки круглого сечения

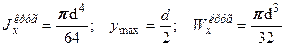. (9.21)

В рассмотренном выше случае изгибающий момент действовал относительно главной центральной оси, совпадающей с нейтральной линией. При этом плоскость действия момента (силовая плоскость) совпадает с одной из главных плоскостей. Если положение силовой плоскости и главной плоскости балки при деформациях не меняются, то, как указано выше, имеет место чистый прямой изгиб и все деформации происходят в одной плоскости.

Из формулы (9.18) следует, что нормальные напряжения при чистом изгибе распределяются по линейному закону пропорционально расстоянию от нейтральной линии, следователь, наиболее нагруженными будут внешние волокна сечения. Поэтому при проектировании оптимальных с точки зрения веса конструкций, работающих на изгиб, стремятся основную часть площади сечения максимально удалить от нейтральной линии. В этом случае возрастают моменты инерции и сопротивления относительно рассматриваемой оси. В авиастроении широко применяются профили двутаврового и швеллерного сечений.

Наличие концентраторов напряжений (изменение формы профиля, отверстия, вырезы и др.) требует коррекции полученных расчетных формул. Например, для хрупких материалов используется соотношение

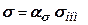, (9.22)

где σ_ном – нормальные напряжения в рассматриваемой точке, определенные по приведенным выше формулам сопротивления материалов;

α_σ – коэффициент концентрации напряжений, который приводится в справочниках.