Сила давления на цилиндрическую стенку
В общем случае какой угодно криволинейной поверхности, расположенной внутри жидкости, действие сил гидростатического давления на такую поверхность приводится к равнодействующей и моменту пары сил. В частном случае наиболее распространенных в технике цилиндрической и сферической поверхностей сила давления сводится (в силу симметрии) к одной равнодействующей силе. Определим эту силу для цилиндрической поверхности, расположенной в толще жидкости (рис. 2.9).
Выделим на рассматриваемой цилиндрической поверхности малый элемент площади dω, кривизной которого можно пренебречь.
Тогда для случая плоской стенки формула нами уже выведена:
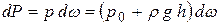 .
.
Разложим эту силу на вертикальную и горизонтальную составляющие:
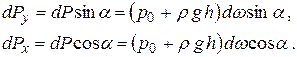
Из рис.2.9 видно, что проекции элементарной площадки на соответствующие оси координат выразятся следующим образом:
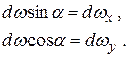
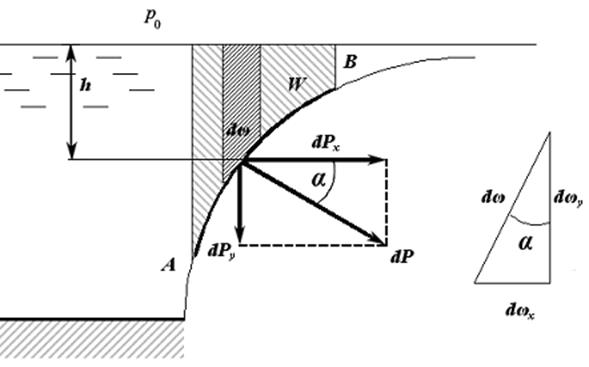
Рис. 2.9
Следовательно,
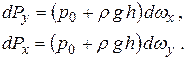
Для нахождения силы, действующей на всю площадку, проинтегрируем силы, действующие на элементарные площадки.
Горизонтальная составляющая
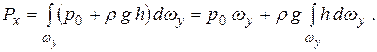 | (2.15) |
Интегрирование проводится по площади проекции всей цилиндрической поверхности AB на вертикальную плоскость, обозначим ее ωy. Второе слагаемое в формуле (2.15) – это статический момент площади ωy относительно оси, перпендикулярной плоскости чертежа. Представим его в виде:
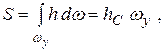
где hC – глубина погружения центра тяжести площадки ωy. Тогда
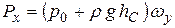
Вертикальная составляющая
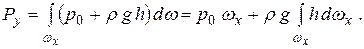 | (2.16) |
Здесь ωx – проекция цилиндрической поверхности АВ на горизонтальную плоскость. Подынтегральное произведение 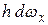 во втором слагаемом формулы (2.16) представляет собой элементарный объем, заштрихованный на рис. 2.9, а значение интеграла равно всему объему жидкости W, находящемуся над поверхностью АВ (на рисунке он показан крупной штриховкой). Жидкость, находящаяся в объеме W, называется телом давления. Таким образом,
во втором слагаемом формулы (2.16) представляет собой элементарный объем, заштрихованный на рис. 2.9, а значение интеграла равно всему объему жидкости W, находящемуся над поверхностью АВ (на рисунке он показан крупной штриховкой). Жидкость, находящаяся в объеме W, называется телом давления. Таким образом,
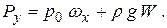
Полная сила P гидростатического давления на цилиндрическую поверхность определяется составляющими Px и Py, складываемыми по правилу параллелограмма:
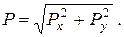
Направление силы P определится углом β:
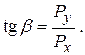
Для цилиндрической поверхности сила P всегда проходит через центр кривизны (ось цилиндра), так как все элементарные составляющие перпендикулярны поверхности стенки и проходят через ее центр тяжести.
При практическом определении вертикальной составляющей силы гидростатического давления существует правило, по которому находится объем тела давления. Объем тела давления ограничен самой цилиндрической поверхностью, двумя вертикальными плоскостями, проходящими через концы цилиндрической поверхности до свободной поверхности жидкости (в случае нахождения жидкости внутри цилиндра, рис. 2.10.а) или до ее продолжения (в случае нахождения жидкости вне цилиндра, рис. 2.10.б).
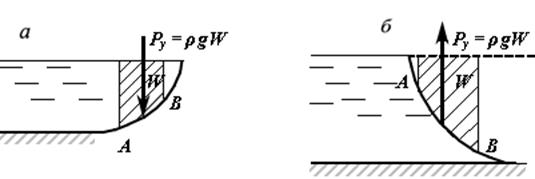
Рис. 2.10
Из рис. 2.10 видно, что в первом случае объем тела давления находится внутри жидкости (действительное тело давления), а во втором – вне ее (фиктивное тело давления). Направления вертикальных составляющих оказываются противоположными, а величина их равна весу жидкости, находящейся в теле давления.
