Сложение двух параллельных сил
 Пусть параллельные и одинаково направленные силы F1иF2 приложены к точкам А и В тела и нужно найти их равнодействующую. Приложим к точкам А и В равные по модулю и противоположно направленные силы Q1 и Q2 (их модуль может быть любым); такое добавление можно сделать на основании аксиомы 2. Тогда в точках А и В мы получим две силы R1и R2:
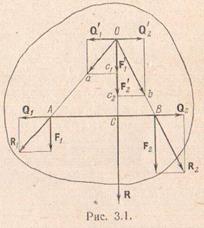
Пусть параллельные и одинаково направленные силы F1иF2 приложены к точкам А и В тела и нужно найти их равнодействующую. Приложим к точкам А и В равные по модулю и противоположно направленные силы Q1 и Q2 (их модуль может быть любым); такое добавление можно сделать на основании аксиомы 2. Тогда в точках А и В мы получим две силы R1и R2:
R1=(F1,Q1)и R2=(F2,Q2).
Линии действия этих сил пересекаются в некоторой точке О. Перенесем силы R1и R2 в точку О и разложим каждую на составляющие:
R1=(F'1,Q'1)и R2=(F'2,Q'2).
Из построения видно, что Q'1=Q1и Q'2=Q2, следовательно, Q'1=-Q'2 и эти силы согласно аксиоме 2 можно отбросить. Кроме того, F'1=F1, F'2=F2. Силы F'1 и F'2 действуют по одной прямой, и их можно заменить одной силой
R=F1+F2, (3.1)
которая и будет искомой равнодействующей. Модуль равнодействующей равен
R=F1+F2.
Очевидно, что линия действия равнодействующей параллельна линиям действия слагаемых. Из подобия треугольников Оас1 и ОАС, а, также Obc2 и ОВС получим соотношение
F1/ F2=ВС/АС, (3.2)
 которым определяется точка приложения равнодействующей R. Таким образом, система двух параллельных сил, направленных в одну сторону, имеет равнодействующую, параллельную этим силам, причем ее модуль равен сумме слагаемых; линия действия равнодействующей делит расстояние между точками приложения слагаемых сил внутренним образом на части, обратно пропорциональные модулям этих сил.
которым определяется точка приложения равнодействующей R. Таким образом, система двух параллельных сил, направленных в одну сторону, имеет равнодействующую, параллельную этим силам, причем ее модуль равен сумме слагаемых; линия действия равнодействующей делит расстояние между точками приложения слагаемых сил внутренним образом на части, обратно пропорциональные модулям этих сил.
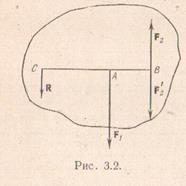
Рассмотрим теперь задачу о сложении двух параллельных сил, направленных в разные стороны и не равных друг другу по модулю. Пусть даны две силы F1иF2, причем для определенности будем считать, что F1> F2.
Пользуясь формулами (3.1) и (3.2), можно силу F1 разложить на две составляющие, F'2и R, направленные в сторону силы F1. Сделаем это так, чтобы сила F'2 оказалась приложенной к точке В, и положим F'2=- F2.
Таким образом, (F1,F2)=(R, F'2, F2). Теперь заметим, что силы F2, F'2 можно отбросить как эквивалентные нулю (аксиома 2), следовательно, (F1,F2)=R, т.е. сила Rи является равнодействующей. Определим силу R, удовлетворяющую такому разложению силы F1. Формулы (3.1) и (3.2) дают
R+ F'2=F1,  R/ F2=АВ/АС. (3.3)
R/ F2=АВ/АС. (3.3)
Отсюда следует
R=F1-F'2=F1+F2,
и так как силы F1иF2 направлены в разные стороны, то
R=F1-F2. (3.4)
Подставим это выражение в формулу (3.3), получим после простых преобразований
F1/ F2=ВС/АС.
Из двух последних формул следует, что две не равные по модулю противоположно направленные параллельные силы имеют равнодействующую, параллельную этим силам, причем ее модуль равен разности модулей слагаемых; линия действия равнодействующей делит расстояние между точками приложения слагаемых сил внешним образом на части, обратно пропорциональные модулям этих сил. Заметим, что равнодействующая в этом случае всегда расположена за большей из двух сил.
Прежде чем рассмотреть случай двух равных по модулю, параллельных, но противоположно направленных сил, заметим, что из равенств (3.3) и (3.4) следует
АС= F2·АВ/(F1-F2). (3.5)
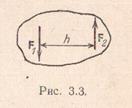 Рассмотрим теперь случай двух параллельных, равных по модулю, но противоположно направленных сил. Эта система сил называется парой силой или просто парой и обозначается символом (F1,F2). Рассуждения, которыми мы пользовались при выводе соотношений (3.4) и (3.5), здесь непригодны. Формальное применение этих соотношений приводит к заключению, что в данном случае модуль равнодействующей равен нулю, а линия ее действия находится на бесконечном удалении от линий действия слагаемых сил. Чтобы понять природу этого результата, вновь вернемся к случаю, когда слагаемые силы имеют различные модули, и предположим, что модуль F2 постепенно возрастает, приближаясь к значению модуля F1. Тогда разность модулей будет стремиться к нулю, а система сил (F1,F2) – к паре. При этом модуль равнодействующей будет неограниченно приближаться к нулю, а линия ее действия – неограниченно удаляться от линий действия слагаемых (см. (3.5)).
Рассмотрим теперь случай двух параллельных, равных по модулю, но противоположно направленных сил. Эта система сил называется парой силой или просто парой и обозначается символом (F1,F2). Рассуждения, которыми мы пользовались при выводе соотношений (3.4) и (3.5), здесь непригодны. Формальное применение этих соотношений приводит к заключению, что в данном случае модуль равнодействующей равен нулю, а линия ее действия находится на бесконечном удалении от линий действия слагаемых сил. Чтобы понять природу этого результата, вновь вернемся к случаю, когда слагаемые силы имеют различные модули, и предположим, что модуль F2 постепенно возрастает, приближаясь к значению модуля F1. Тогда разность модулей будет стремиться к нулю, а система сил (F1,F2) – к паре. При этом модуль равнодействующей будет неограниченно приближаться к нулю, а линия ее действия – неограниченно удаляться от линий действия слагаемых (см. (3.5)).
Как следует из сказанного, для пары сил понятие равнодействующей лишено смысла, так как она представляет неуравновешенную систему, которая не может быть заменена одной силой.Говорят, что пара сил не имеет равнодействующей.
Таким образом, пара сил является неприводимым (неупрощаемым) элементом статики; наряду с силой она является вторым самостоятельным элементом статики.
