Запись и решение СЛАУ в матричном виде. Матричные уравнения

Рассмотрим СЛАУ размеренности :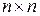

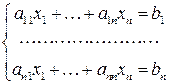(1)

или в матричной форме

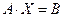, (2)

где матрица 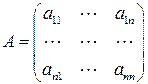системы является квадратной.

Пусть матрица 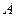– невырожденная, т.е. 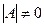, тогда существует 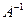; умножим левую и правую части (1.16) слева на 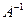, получим 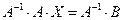или

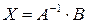. (3)

Пример 1. Решить систему уравнений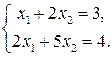

Решение.1) , , .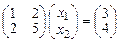

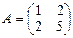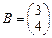2) Определитель матрицы : .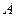

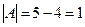3) Найдем . , , .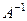

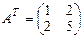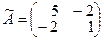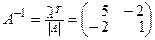4)Тогда .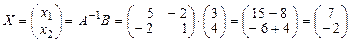

5) Сделаем проверку: 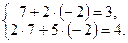Таким образом, ,

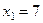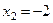
Пример 2.Швейная фабрика в течение трёх дней производила костюмы, плащи и куртки. Известны объёмы выпуска продукции за три дня и денежные затраты на производство за эти дни:

День	Объём выпуска продукции (единиц)	Затраты (тыс. усл. ед.)
Костюмы	Плащи	Куртки
1-й
2-й
3-й

Найти себестоимость единицы продукции каждого вида.

Обозначим: 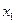– себестоимость костюма,

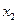– себестоимость плаща,

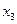– себестоимость куртки.

Получим следующую систему:

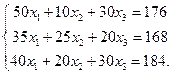
Матрица системы имеет вид:

,

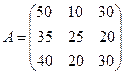вычислим её определитель:

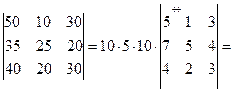
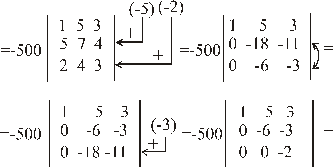
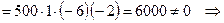
матрица невырожденная. Найдём обратную матрицу.

,

,

,

,

,

,

,

.

.

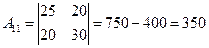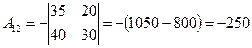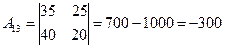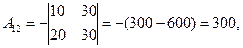
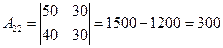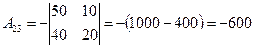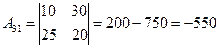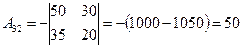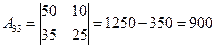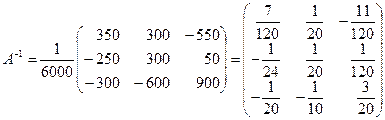Тогда

.

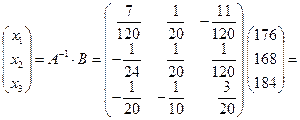
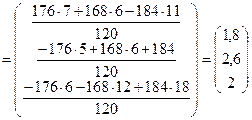Проверка

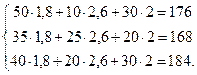
Ответ.Себестоимость костюма – 1,8 тыс. усл. ед., плаща – 2,6 тыс. усл. ед., куртки – 2 тыс. усл. ед.

С помощью обратной матрицы можно решать матричные уравнения.

Пример 3.Решить матричное уравнени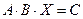е: , где

, , .

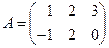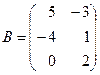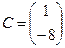Уравнение можно записать в ви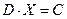де:

, где .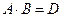

Если 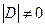, то 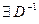, тогда 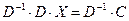, следовательно, .

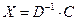Итак, найдём матрицу :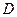

.

.

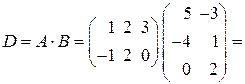
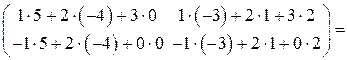
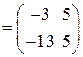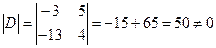Найдём 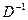: 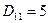, , 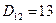, , 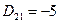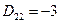тогда

.

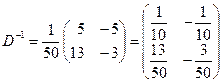Теперь вычислим :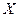

.

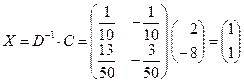Лекция 8

Решение СЛАУ по формулам Крамера.

Пусть дана СЛАУ

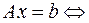
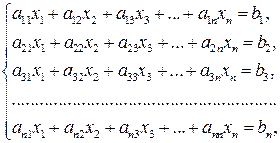
(12.1)

где 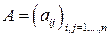– основная матрица системы, , .

Введем в рассмотрение следующие определители 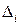( 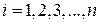): заменим в определителе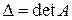 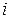-столбец на столбец свободных коэффициентов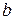

, , …,

.

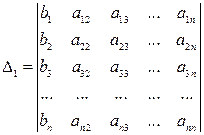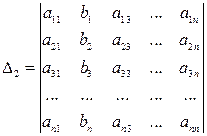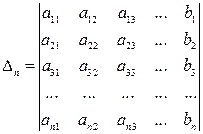Теорема (Формулы Крамера). Если основная матрица 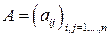системы (12.1) является неособенной квадратной матрицей ( 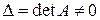), то система (12.1) имеет единственное решение, которое можно вычислить по следующим формулам Крамера:

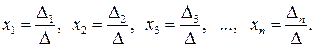(12.2)

Доказательство. Рассмотрим определители 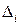( 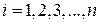). Разложим определитель 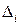по 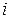-му столбцу (теорема Лапласа):

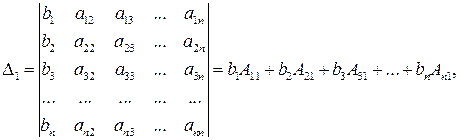(разложение по первому столбцу),

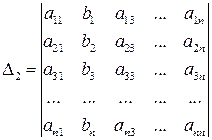
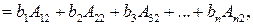(разложение по второму столбцу),

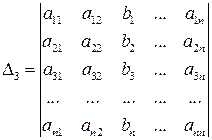
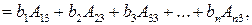(разложение по третьему столбцу),

………………………………………………………………..

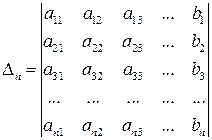
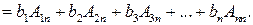(разложение по последнему столбцу).

Так как по условию 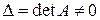, то решение системы (12.1) существует, единственно, и его можно найти матричным способом (через обратную матрицу). Найдем это решение и сведем к нашим исходным данным:

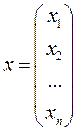
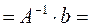
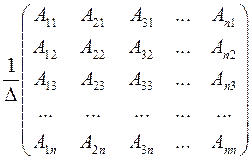
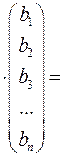
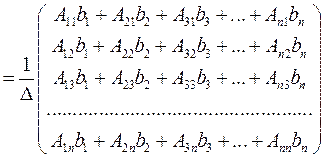
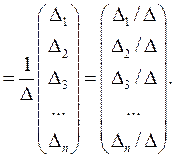
Итак, .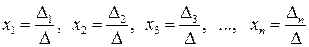

Пример. Найти решение системы уравнений:

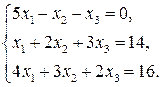
Решение.

D = 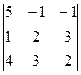= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

D₁ = 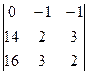= (28 – 48) – (42 – 32) = -20 – 10 = -30,

D₂ = 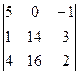= 5(28 – 48) – (16 – 56) = -100 + 40 = -60,

D₃ = 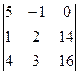= 5( 32 – 42) + (16 – 56) = -50 – 40 = -90,

x₁ = D₁/D = 1; x₂ = D₂/D = 2; x₃ = D₃/D = 3.

Лекция 9

Метод исключения переменных Гаусса для решения СЛАУ: теорема Кронекера-Капелли. Условие единственности решения СЛАУ. Условия несовместности СЛАУ.

Метод исключения переменных Гаусса для решения СЛАУ. Условия существования множества решений СЛАУ (нахождение общего решения СЛАУ).

13. Метод исключения переменных Гаусса для решения СЛАУ:

Теорема Кронекера-Капелли. Условие единственности решения СЛАУ.