Начальные понятия физики в 3-4 и 5-6 классах
Рассмотрим, с какими физическими понятиями можно познакомить учащихся в процессе обучения в 3-4 и 5-6 классах.
Одной из приоритетных тенденций современного образования является создание межпредметных связей при изучении отдельных циклов школьных предметов. Математика имеет самые тесные межпредметные связи с физикой. На уроках математики в 5 классе учителю важно рассказать учащимся о физике, которую они начнут изучать через два года, объяснить, что для успешного изучения физики необходимы прочные знания по математике. Здесь учителю поможет книга, написанная Александром Евсеевичем Гуревичем совместно с Дмитрием Аркадьевичем Исаевым и Любовью Семеновной Понтак, «Физика и химия 5-6 класс». Данная книга поможет сформировать начальное представление о физике и химии, объяснить с научной точки зрения основные природные явления, научить обращаться с простейшими техническими устройствами.
Чтобы показать пятиклассникам значимость качественных знаний по математике для успешного изучения в дальнейшем физики, учителю на уроках математики, особое внимание необходимо уделить таким темам:
5 класс
§ «Буквенные выражения»;
§ «Формулы»;
§ «Формула площади прямоугольника»;
§ «Прямоугольный параллелепипед»;
§ «Обыкновенные дроби»;
§ «Десятичные дроби».
6 класс
• «Проценты»;
• «Пропорции»;
• «Отрицательные числа».
Рекомендуется провести эти уроки в кабинете физики.
В пятом классе во многих рабочих программах по математике рекомендовано изучать тему «Буквенные выражения» три часа. Поэтому целесообразно смоделировать из вышеизложенной разработки («Буквенные выражения») два урока, а на третьем уроке рассказать о физике – науке, которая «дружит» с математикой. С разработкой данного урока вы можете познакомиться в приложении к данному выступлению.
На тему «Формулы» в пятом классе отводится два часа. Рекомендуем дополнить ваши разработки следующим.
· При решении задач на движение напомните своим ученикам, что наука «физика» также изучает механические явления. Скорость, пройденный путь, время движения – это физические характеристики движущегося объекта.
· Рассматривайте встречное движение и движение в одну сторону как разные виды задач, имеющие свой алгоритм решения.
· Отрабатывайте навыки перевода единиц измерения длины, времени, скорости. Например: 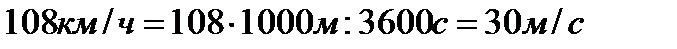 , и наоборот:
, и наоборот: 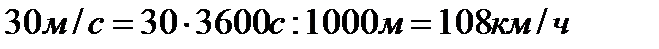 .
.
При изучении темы «Формула площади прямоугольника» обратите внимание учеников на схожесть формул нахождения площади ( 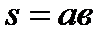 ) и скорости (
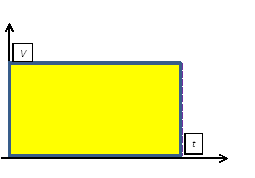
) и скорости ( 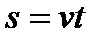 ). Если графически отобразить скорость равномерного движения тела и время движения, то, чтобы найти пройденный путь некоторым объектом, достаточно определить площадь полученного прямоугольника.
). Если графически отобразить скорость равномерного движения тела и время движения, то, чтобы найти пройденный путь некоторым объектом, достаточно определить площадь полученного прямоугольника.
При изучении темы «Прямоугольный параллелепипед» и «Объемы. Объем прямоугольного параллелепипеда»необходимо:
· Изучить дополнительный материал об истории открытия закона Архимеда и провести эксперимент для лучшего понимания данного закона.
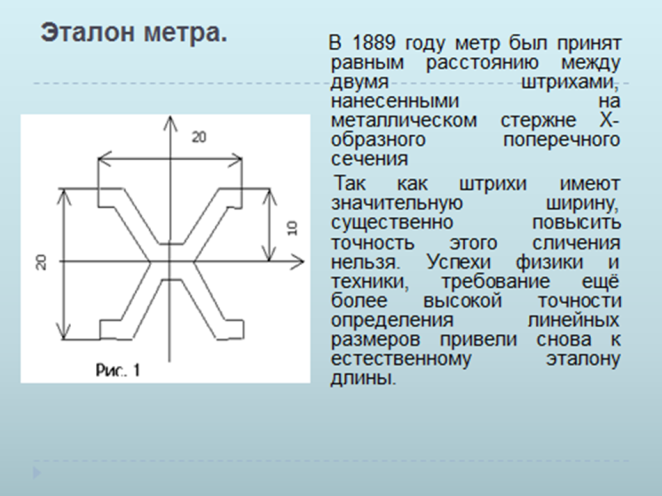
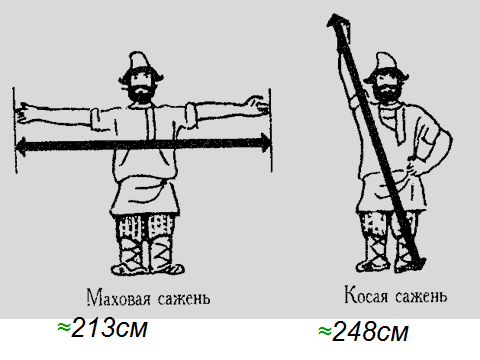
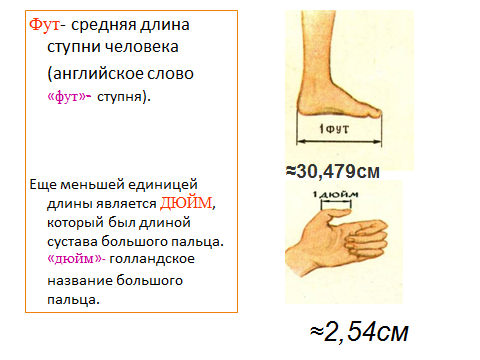
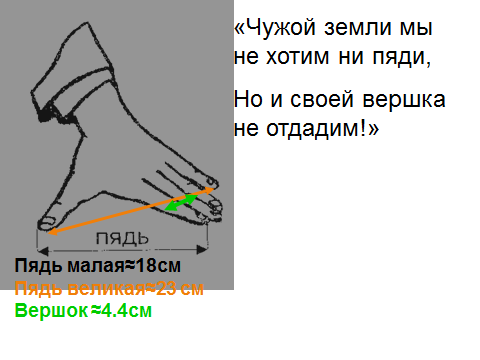
· Познакомить с эталонами массы и длины, изучить историю мер единиц измерения. Целесообразно организовать изучение данного материала посредством проектной деятельности. На пример, творческие проекты «Меры измерений: от древности и до наших дней».
 |  |
 |  |
 |  |
 |  |
 |
· Уделить внимание отработке навыков перевода единиц объема, показав зависимость между такими единицами, как литр, миллилитр, дециметр, сантиметр. (1 литр =1 дм3,1 мл = 1см3).
· Ввести понятие плотности. Плотность – это физическая величина, показывающая чему равна масса вещества в единице объема. Научить переводить единицы плотности: 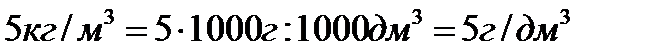 . Провести эксперимент по определению плотности вещества. Для этого понадобятся предметы небольших размеров в форме прямоугольного параллелепипеда, электронные или рычажные весы. Необходимо измерить массу параллелепипеда, его длину, ширину и высоту. Вычислить объем параллелепипеда по формуле. Разделить массу на объем и так определить плотность вещества, из которого изготовлен параллелепипед.
. Провести эксперимент по определению плотности вещества. Для этого понадобятся предметы небольших размеров в форме прямоугольного параллелепипеда, электронные или рычажные весы. Необходимо измерить массу параллелепипеда, его длину, ширину и высоту. Вычислить объем параллелепипеда по формуле. Разделить массу на объем и так определить плотность вещества, из которого изготовлен параллелепипед.
| Оборудование: предметы маленьких размеров в форме прямоугольного параллелепипеда, электронные или рычажные весы. |
Выполнение работы проиллюстрировать 1) Измерить массу параллелепипеда. 2) Измерить длину ширину и высоту параллелепипеда. 3) Вычислить объем параллелепипеда по формуле 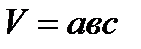 . 4) Разделить массу на объем и так найти плотность вещества, из которого изготовлен параллелепипед. . 4) Разделить массу на объем и так найти плотность вещества, из которого изготовлен параллелепипед. |
Понятие десятичной дроби у пятиклассников складывается в течение всей третьей четверти. Поэтому учитель легко сможет найти время для разрешения на этих уроках таких вопросов физического характера как:
· использование десятичных и обыкновенных дробей в задачах на движение;
· выражение единиц измерения массы, длины, площади, объема и времени в дольных и кратных единицах;
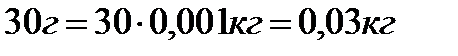 ,
,
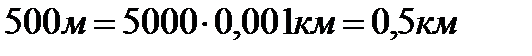 ,
,
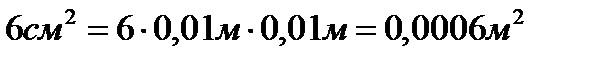 ,
,
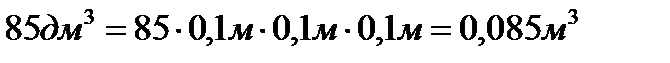 ,
,
3л = 3 дм3,
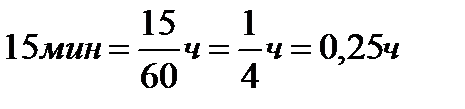 .
.
· отработка навыков перевода единиц измерения скорости и плотности;
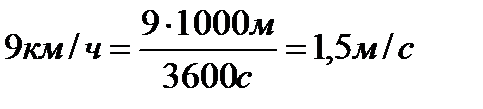 ,
,
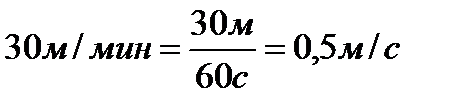 ,
,
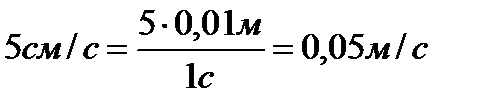 ,
,
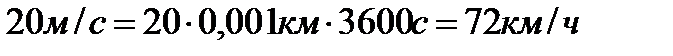 ,
, 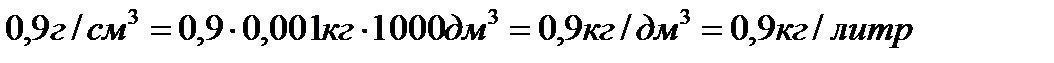 .
.
· решение простейших задач на движение с использованием чертежа;
Задача: За 10 минут заяц-русак пробегает путь 12 км. Определите его скорость.
Дано: Решение:
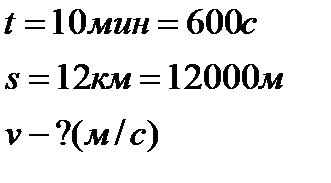
 . Ответ: 20 м/с.
. Ответ: 20 м/с.
· сравнение десятичных дробей как не просто чисел, а как физических измерений Например: 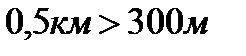 ,
, 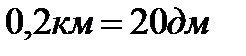 ;
;
· изучение темы «Сложение и вычитание десятичных дробей» можно рассматривать сложение и вычитание физических единиц измерения; Например: 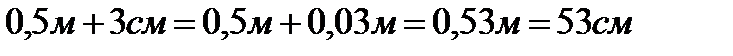 ;
;
· рассмотрение в качестве буквенных выражений с одной известной величиной формулы определения пути. Например: 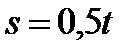 , где
, где 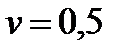 . И, наоборот:
. И, наоборот: 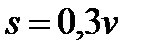 , здесь
, здесь 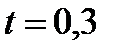 .
.
На уроках математики при решении задач по теме «Проценты»рекомендуем ввести термин «КПД. Коэффициент полезного действия».
В учебниках по физике для седьмого класса определение КПД звучит так: «Чтобы найти КПД механизма, надо полезную работу разделить на ту, которая была затрачена при использовании данного механизма». 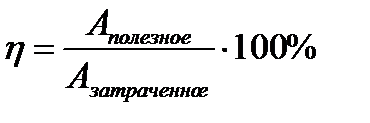 .
.
Можно решить задачу следующего содержания: «При подъеме груза массой 20 кг на 4 метра механизму необходимо иметь энергию 800 Джоулей. Чему равен КПД механизма, который совершил при этом работу равную 1000 Джоулям?». Следует сказать ученикам, что энергия затрачивается при совершении работы и обе эти величины измеряют в Джоулях. Далее в терминологию физики можно не углубляться.
Если позволяет время, то можно провести и экспериментальную работу по определению КПД. Рекомендуем сначала учителю ход эксперимента изучить из учебника по физике для 7 класса.
При изучении темы «Пропорции» в шестом классе нужно рассказать о правиле моментов и использовании рычага. Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки, - это правило называют правилом моментов. Также описываемое пропорциональное соотношение используется при машиностроении, так понятие пропорции лежит в основе создания гидравлического пресса.
Задача: Площадь меньшего поршня гидравлической машины 10 см2, и на него действует сила в 200 Н. Площадь большого поршня равна 200см2. Какая сила действует на большой поршень?
Решение:
S1=10 см2; F1=200H; S2=200см2; F2-?
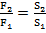 ; F2·S1=F1·S2;
; F2·S1=F1·S2; 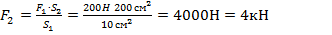
Ответ: F2= 4кН.
При изучении темы «Положительные и отрицательные числа» в 6 классе следует обратить внимание учеников на то, что в физике отрицательными числами можно описать следующее:
• температура ниже таяния льда или замерзания воды;
• скорость объекта, который движется навстречу наблюдателю;
• электрический заряд;
• ускорение тела при замедленном движении;
• время до начала наблюдения некоторого физического процесса.
Необходимо акцентировать внимание, что в географии отрицательными числами измеряют глубины, расположенные ниже уровня воды. При изучении истории используют ленту времени, на которой отрицательной считается дата, где событие произошло до нашей эры.
| Перед вами ЛИНИЯ ВРЕМЕНИ, отметьте на ней следующие события из истории математики: | |
| Книга «Начала» была написана Евклидом в 3 в до н.э. | |
| Теория чисел зародилась в Др. Греции в 6 в. до н.э. | |
| Десятичные дроби появились в Китае в 3 в. н.э. | |
| Теория отношений и пропорций была разработана в Др. Греции в 4 в. до н.э. | |
| Позиционная десятичная система счисления распространилась в странах Востока в 9 в н.э. |
В биологии и медицине патологию зрения выражают отрицательными и положительными числами.
Чтобы изучить досконально использование отрицательных чисел в разных областях необходимо разрабатывать исследовательские проекты по заданной тематике.
«Координатная плоскость» изучается в конце темы «Положительные и отрицательные числа» и является прикладной, что вызывает у учащихся живой интерес при изучении. Общаясь друг с другом, люди часто говорят: "Оставьте свои координаты". Для чего? Чтобы человека было легко найти. Это могут быть: номер телефона, домашний адрес, место работы. Суть координат или системы координат состоит в том, что существует правило, по которому определяется положение объекта. Чтобы правильно занять свое место в кинотеатре нужно знать две координаты - ряд и место. Система географических координат (широта - параллели и долгота -меридианы). Те, кто в детстве играл в морской бой, тоже помнят, что каждая клетка на игровом поле определялась двумя координатами - буквой и цифрой. Системы координат пронизывают всю практическую жизнь человека.
В пятом классе во многих рабочих программах по математике на изучение темы «Круговые диаграммы» отводится два часа. В шестом классе тему «Столбчатые диаграммы» изучают также два часа.
В шестом классе можно построить столбчатую диаграмму при описании движения и обратить внимание учеников на то, что зависимость можно показать и с помощью графика, и с помощью диаграммы.
Например, «На соревнованиях по плаванию в 50-метровом бассейне спортсмен проплыл 100-метровую дистанцию. На рисунке изображен график зависимости расстояния между спортсменом и точкой старта от времени движения спортсмена. Постройте соответствующую диаграмму».
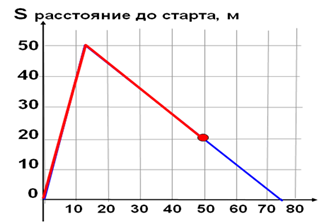
Решение:
В 3-4 классах при изучении тем «Скорость. Время. Путь» необходимо создать условия для осмысления понятия «скорость», сформировать первоначальные представления о скорости как величине, показывающей, какой путь проходит движущийся предмет за единицу времени. Поэтому необходимо раскрыть следующие вопросы:
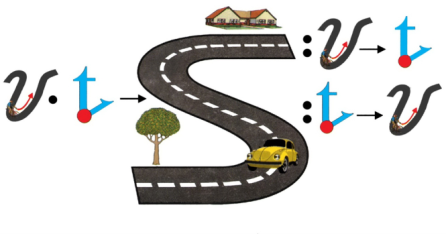
· общепринятые буквенные обозначения. Скорость обозначается строчной буквой V. В переводе с английского языка velositi – скорость. Taim в переводе с английского языка – время, значит обозначаем буквой – t. Расстояние обозначается латинской буквой S, т.к. spaisпо-английски –расстояние.
 |  |
 |
· обратить внимание на то, как графически показан путь, как графически показана скорость. Что показывают точки на луче? Расстояние от точки до точки равно расстоянию за единицу времени, количество точек соответствует времени движения. Теперь можно, например, решить следующую задачу.
Задача. Велосипедист едет со скоростью v=15 км/ч. Покажи его движение на числовом луче. Какое расстояние преодолеет велосипедист за 1 ч, 2 ч, 3 ч, t ч? Заполни таблицу и напиши формулу, выражающую зависимость пройденного расстояния s от времени t.
Решение:
 |  |
При этом можно пользоваться этой опорной карточкой.
| Время (t, ч) | t | |||
| Расстояние (s,км) |
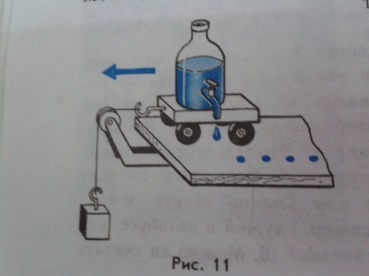
Для того, чтобы дети осознали скорость как величину, характеризующую движение, можно провести опыт. Установим на тележку капельницу. Из капельницы через одинаковые промежутки времени падают капли окрашенной жидкости. Присоединим к тележке груз, перекинув через блок. При движении тележки расстояния между следами, оставленными каплями на бумаге, могут быть равны. Это означает, что тележка за равные промежутки времени проходит равные пути. Повернув кран капельницы так, чтобы капли падали чаще, повторим опыт. Следы капель и теперь оказываются на равных расстояниях друг от друга, хотя и меньших, чем в первом опыте. Это означает, что и за меньшие равные промежутки времени тележка проходит равные пути. Вывод: скорость показывает, какой путь проходит тело за единицу времени.
Использование межпредметных связей не только поможет показать взаимосвязь между предметами, подготовить учащихся к изучению физики, но и разнообразит уроки математики, расширит их практическую направленность.
