Метод Крамера - вывод формул
Метод Крамера.
Метод Крамера применяется для решения систем линейных алгебраических уравнений (СЛАУ), в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера находятся неизвестные переменные и получим формулы. После этого перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.
При изучении материала Вам может быть полезна статья вычисление определителя матрицы, свойства определителя.
Навигация по странице.
- Метод Крамера - вывод формул.
- Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
- Примеры решения систем линейных алгебраических уравнений методом Крамера.
Метод Крамера - вывод формул.
Пусть нам требуется решить систему линейных уравнений вида
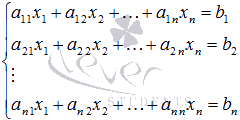
где x1, x2, …, xn – неизвестные переменные, ai j , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b1, b2, …, bn - свободные члены. Решением СЛАУ называется такой набор значений x1, x2, …, xn при которых все уравнения системы обращаются в тождества.
В матричном виде эта система может быть записана как A ⋅ X = B, где 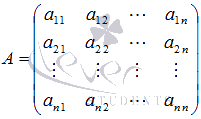 - основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных,
- основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных, 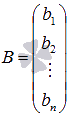 - матрица – столбец свободных членов, а
- матрица – столбец свободных членов, а 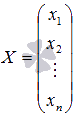 - матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x1, x2, …, xn, матрица
- матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x1, x2, …, xn, матрица 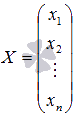 становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество
становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество 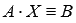 .
.
Будем считать, что матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при 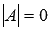 разобраны в разделе решение систем линейных алгебраических уравнений).
разобраны в разделе решение систем линейных алгебраических уравнений).
Метод Крамера основывается на двух свойствах определителя матрицы:
1. Определитель квадратной матрицы  равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения:
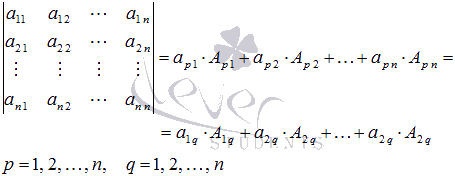
2. Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю:
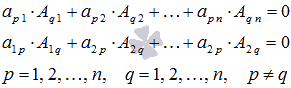
Итак, приступим к нахождению неизвестной переменной x1. Для этого умножим обе части первого уравнения системы на А1 1 , обе части второго уравнения – на А2 1 , и так далее, обе части n-ого уравнения – на Аn 1 (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А):
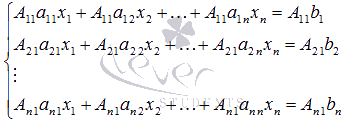
Сложим все левые части уравнения системы, сгруппировав слагаемые при неизвестных переменных x1, x2, …, xn, и приравняем эту сумму к сумме всех правых частей уравнений:
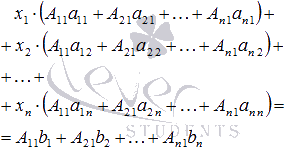
Если обратиться к озвученным ранее свойствам определителя, то имеем

и предыдущее равенство примет вид
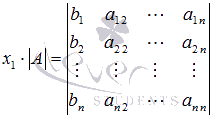
откуда
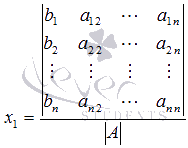
Аналогично находим x2. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А:
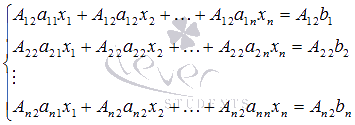
Складываем все уравнения системы, группируем слагаемые при неизвестных переменных x1, x2, …, xn и применяем свойства определителя:

Откуда
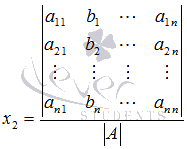 .
.
Аналогично находятся оставшиеся неизвестные переменные.
Если обозначить
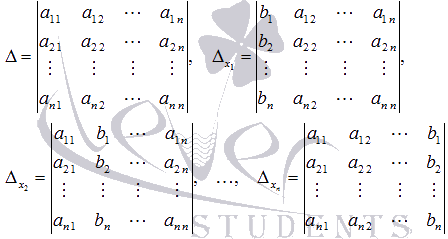
то получаем формулы для нахождения неизвестных переменных по методу Крамера 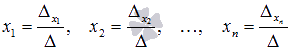 .
.
Замечание.
Если система линейных алгебраических уравнений однородная, то есть 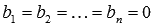 , то она имеет лишь тривиальное решение
, то она имеет лишь тривиальное решение 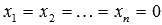 (при
(при 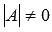 ). Действительно, при нулевых свободных членах все определители
). Действительно, при нулевых свободных членах все определители 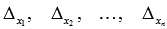 будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы
будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы 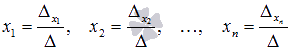 дадут
дадут 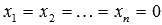 .
.
К началу страницы
