Пример выполнения заданий

1. Построение полинома Лагранжа для таблично заданной функции.

Построить интерполяционный многочлен Лагранжа для функции, заданной в табл. 6.1.

Таблица 6.1

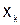	1.1	1.5	2.0	2.6
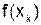	0.0953	0.4055	0.6931	0.9555

Используя полученный интерполяционный многочлен, вычислить приближённо значение в точке .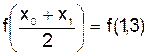

Для построения интерполяционного многочлена используем формулу (6.3) при 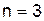. В результате получаем многочлен третьей степени 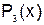, который в узлах интерполяции совпадает с табличными значениями исходной функции:

.

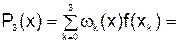
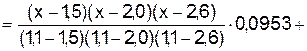
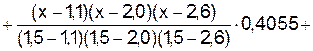
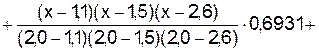
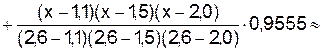
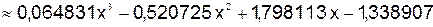Проверяем условия :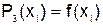

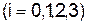1) .

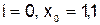Подставляем 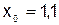в полученный многочлен:

;

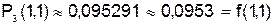2) :

;

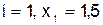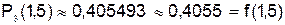3) :

;

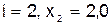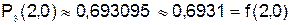4) :

.

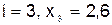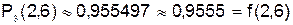Вычисляем , .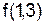

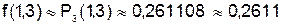Построение полинома Лагранжа в пакете MATHCAD.

Построение дробно-рациональных функций Лагранжа с использованием программного блока:

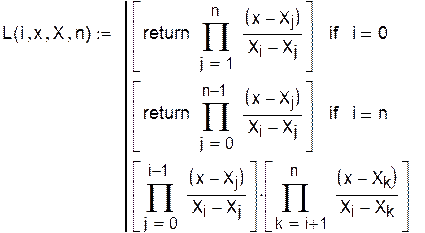
Полином Лагранжа можно записать так:

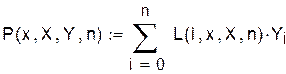
Проверка основного условия интерполяции:

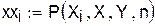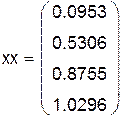График полученных результатов может быть таким:

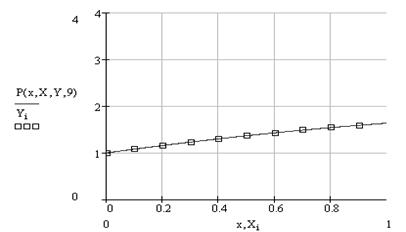
Полином Лагранжа можно записать и по-другому:

,

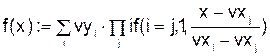гдеvx, vy – векторы, заданные табличные значения.

Пример построения полинома Лагранжа в пакете MATLAB.

function yy=lagrange(x,y,xx)

% число узлов интерполяции

N=length(x);

% число узлов, в которых высчитывается значение интерполяционного полинома

N_res=length(xx);

% создание нулевого массива значений интерполяционного полинома

yy=zeros(size(xx));

for k=1:N

% вычисление функции Лагранжа Li(X)

Li=ones(size(xx));

for j=[1:k-1, k+1:N]

for i=[1:N_res]

Li(i)=Li(i).*(xx(i)-x(j))/(x(k)-x(j));

end

end

% накопление суммы

yy = yy + y(k)*Li;

yy

end

Пример использования узлов Чебышева.

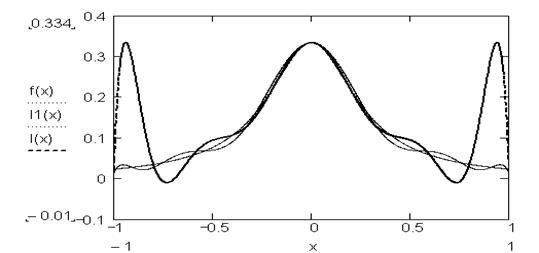
Заданная функция f(x) табулируется на интервале [-1,1] двумя способами: с шагом 0.2 и в узлах Чебышева. На двух полученных сетках строятся полиномы Лагранжа. Результаты визуализируются с помощью графиков. На графике, приведенном ниже, видно значительное отклонение полинома Лагранжа, построенного на сетке с шагом 0.2, от исходной функции и более приемлемое приближение функции для полинома, построенного на узлах Чебышева:

исходная функция:

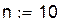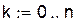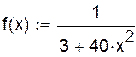Узлы Чебышева:

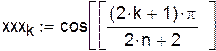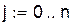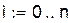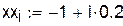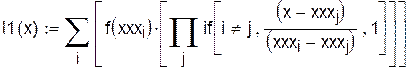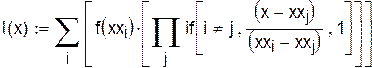Пример вычисления погрешности интерполирования.

Анализ погрешности замены исходной функции интерполяционным многочленом для таблиц с постоянным шагом:

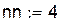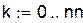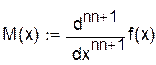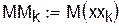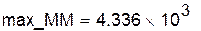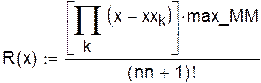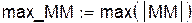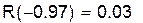Варианты лабораторных работ

Номер варианта	Исходные данные
	x f(x)	1,4 0,3365	1,8 0.5878	2,3 0.8329	2,9 1.0647
	x f(x)	2,0 0,6931	2,5 0.9163	2,8 1.029б	3,3 1,1939
	x f(x)	4,0 1,3863	4,5 1,5041	4,9 1.5892	5,4 1.6864
	x f(x)	1,2 0,1823	1,6 0,4700	2,1 0.7419	2,6 1,6864
	x f(x)	2,2 0,7885	2,7 0,9933	3,1 1.1314	3,6 1,2809

Варианты лабораторных работ (продолжение)

Номер варианта	Исходные данные
	x f(x)	3,2 1,1632	3,6 1.2809	4,1 1,4110	4,6 1.5261
	x f(x)	3,4 1,2238	3,9 1,3610	4.3 1,4586	4,9 1.5861
	x f(x)	1,6 0,4700	2,1 0,7419	2,7 0,9933	8,2 1,1632
	x f(x)	2,8 1,0296	3,1 1.1314	3,7 1,3083	4,2 1,4351
	x f(x)	3,1 1,1314	3,6 1,2809	4,0 1,З863	4,6 1,5261
	x f(x)	1,9 0,6419	2,5 0,9163	2,9 1,0647	3.4 1.2238
	x f(x)	1,7 0,5306	2,2 0,7885	2,8 1.0296	3,2 1.1632
	x f(x)	3,6 1.2809	4,2 1.4351	4,5 1,5041	5.2 1.6094
	x f(x)	2,5 0,9163	2,9 1,0647	3,6 1.2809	4,1 1.4110
	x f(x)	3,3 1,1939	3,9 1,3610	4,4 1,4816	5,0 1,6094
	x f(x)	1,1 0,0953	1,7 0,5306	2,4 0.6755	2,8 1,0296
	x f(x)	2,1 0.7419	2.5 0.9163	3,0 1,0986	3,5 1,2528
	x f(x)	3,2 1,1632	3,7 1.3083	4,3 1,4586	4,9 1,5892
	x f(x)	2,7 0.9933	3,3 1.1939	3,8 1.3350	4,6 1,5261
	x f(x)	1,0 0,0000	1,5 0.4055	2,1 0,7419	2,7 0.9933
	x f(x)	1,4 0,3365	1.9 0,6419	2,6 0,9555	3,0 1,0986
	x f(x)	3,1 1.1314	3.7 1,3083	4,2 1.4351	4.8 1.5686
	x f(x)	2,6 0.9555	3,2 1.1632	4.0 1.3863	4,5 1.5041
	x f(x)	1,6 0.4700	2,2 0,7885	2,7 .9933	8,4 1,2238
	x f(x)	2,1 0,7419	2,7 0,9933	3,3 1.1939	3,8 1.3350

Варианты лабораторных работ (окончание)

Номер варианта	Исходные данные
	x f(x)	2,6 0,9555	3.0 1,0986	1,3610	4,5 1,5041
	x f(x)	4,5 1,5041	4,9 1.5892	5,5 1,7047	6,0 1.7916
	x f(x)	3,5 1,2528	3,8 1,3350	4,5 1,5041	5,1 1.6292
	x f(x)	2,6 1,0296	3,3 1.1939	3,9 1,3610	4,6 1,5261
	x f(x)	4,1 1,4110	4,6 1,5261	5,2 1,6487	6,0 1,7918

Лабораторная работа № 7

ИНТЕРПОЛИРОВАНИЕ ДЛЯ ТАБЛИЦ С ПОСТОЯННЫМ ШАГОМ. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ.