Приведение масс к динамической модели
II Динамический анализ машинного агрегата
Целью динамического анализа является исследование движения машины с учетом сил действующих на ее звенья. Для упрощения этой задачи необходимо представить механизм в виде динамической модели, которая должна учитывать его инерциальные и силовые характеристики, а затем с помощью дифференциального уравнения описать движение этой динамической модели.
Определение масс и моментов инерции звеньев механизма
Определим массы звеньев 1,2 и 4 из заданных соотношений
m/ l =12 (2.1)
где: l – длина звена
Тогда масса кривошипа будет равна:
m1 = 12·l1= 12·0,095=1,14(кг)
где: l1 = 2·r = 0,095(м)
Массу поршней из соотношения
mп=0,04·D (2.2)
где: D – диаметр поршней, (мм).
Тогда диаметр поршня первой ступени будет равен:
m3 = 0,04·D1 = 0,04·146 = 5,84(кг)
Определим моменты инерции звеньев 1, 3 и 4 из заданных соотношений
ISi =0,017·mi· 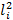 (2.3)
(2.3)
Для звена ОА получим:
IS1 =0,17·m1· 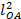 =0,17·1.14·0,0952=0,00175 (кг·м2)
=0,17·1.14·0,0952=0,00175 (кг·м2)
Результат определения масс и моментов инерции всех звеньев механизма представим в виде таблицы 2.1.
Таблица 2.1 Значение масс и моментов инерции звеньев механизма.
| Масса звена, кг | Момент инерции звена, кг·м2 | ||||||
| m1 | m2 | m3 | m4 | m5 | IS1 | IS2 | IS4 |
| 1,14 | 4.64 | 5.84 | 4.64 | 2.56 | 0,00175 | 0,120 | 0,120 |
Приведение масс к динамической модели
Величину приведенного момента инерции всего механизма определяем суммой приведенных моментов инерции отдельных звеньев:
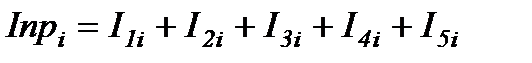 (2.4)
(2.4)
где: 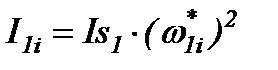 – приведенный момент инерции кривошипа;
– приведенный момент инерции кривошипа;
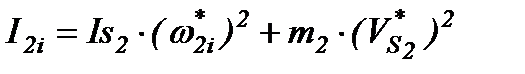 – приведенный момент инерции шатуна 2;
– приведенный момент инерции шатуна 2;
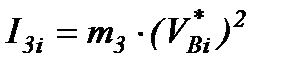 – приведенный момент инерции ползуна 3;
– приведенный момент инерции ползуна 3;
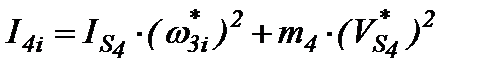 – приведенный момент инерции шатуна 4;
– приведенный момент инерции шатуна 4;
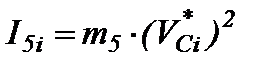 – приведенный момент инерции ползуна 5;
– приведенный момент инерции ползуна 5;
С учетом составляющих формула 2.3 примет вид:
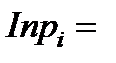
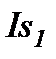 +
+ 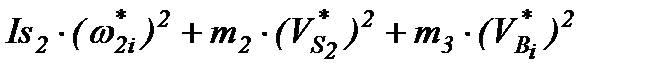 +
+ 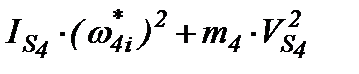 +
+ 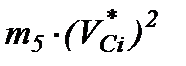 (2.5)
(2.5)
Для нулевого положения механизма находим:
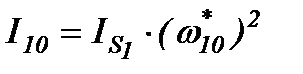 =
= 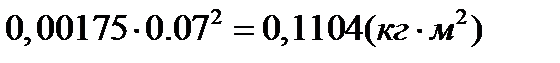
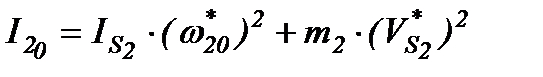 =
= 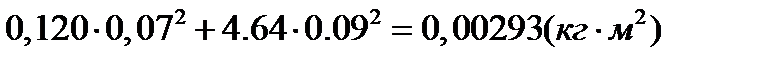
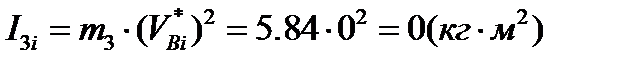
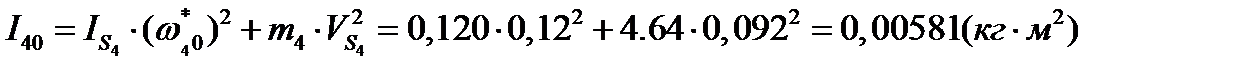
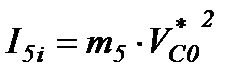
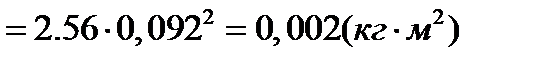
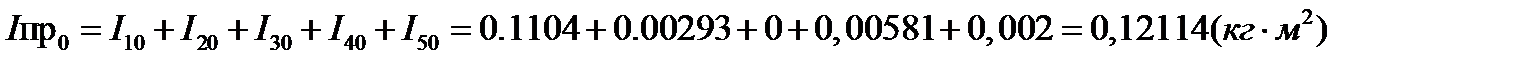
Расчет для остальных положений сносим в таблицу 2.2
Таблица 2.2 Значения приведенного момента инерции
| Угол поворота кривошипа ϕ° | Значения приведенного момента инерции звеньев механизма | ||||||
| Is1,кг м2 | Is2,кг м2 | Is3,кг м2 | Is3,кг м2 | Is4,кг м2 | Ipr,кг м2 | ||
| 0,0018 | 0,0069 | 0,0926 | |||||
| 0,0018 | 0,0053 | 0,00203 | 0,1099 | ||||
| 0,0018 | 0,0017 | 0,00529 | 0,1292 | ||||
| 0,0018 | 0,00691 | 0,1222 | |||||
| 0,0018 | 0,002 | 0,00581 | 0,1082 | ||||
| 0,0018 | 0,0053 | 0,00173 | 0,1009 | ||||
| 0,0018 | 0,0069 | 0,0991 | |||||
| 0,0018 | 0,0058 | 0,00173 | 0,0846 | ||||
| 0,0018 | 0,0017 | 0,00529 | 0,0966 | ||||
| 0,0018 | 0,00691 | 0,1222 | |||||
| 0,0018 | 0,0017 | 0,00529 | 0,1104 | ||||
| 0,0018 | 0,0053 | 0,00173 | 0,0978 | ||||
| 0,0018 | 0,0069 | 0,0926 |
По полученным данным на листе 2 строим график изменения приведенного момента инерции динамической модели Iпр= f(φ) в масштабе:
μIпр = 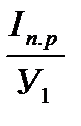 =
= 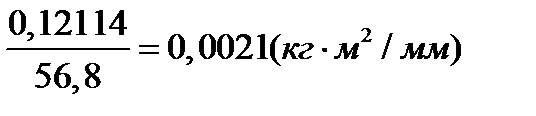 (2.6)
(2.6)
где: УI – отрезок изображающий Iп.р на графике.
Для составления уравнения движения машинного агрегата необходимо приведенный момент инерции представить в виде непрерывной математической функции (ряда Фурье с тремя гармониками ):
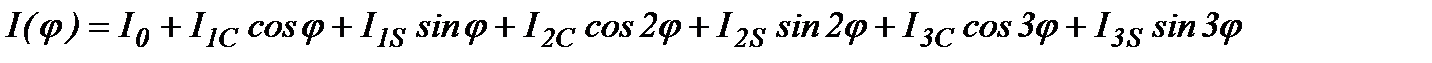 | (2.7) |
где: коэффициенты ряда Фурье определяем по следующим формулам:
постоянная ряда: 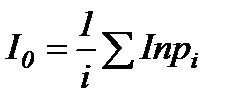 ; (2.8)
; (2.8)
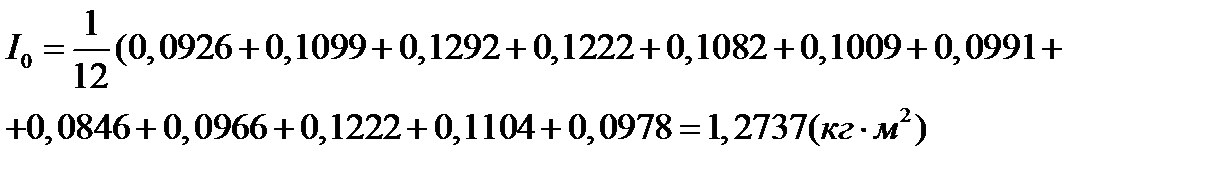
коэффициент при синусах n-ой гармоники :
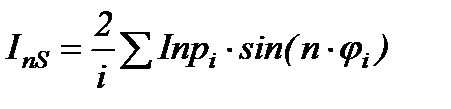 (2.9)
(2.9)
для n=1 получим
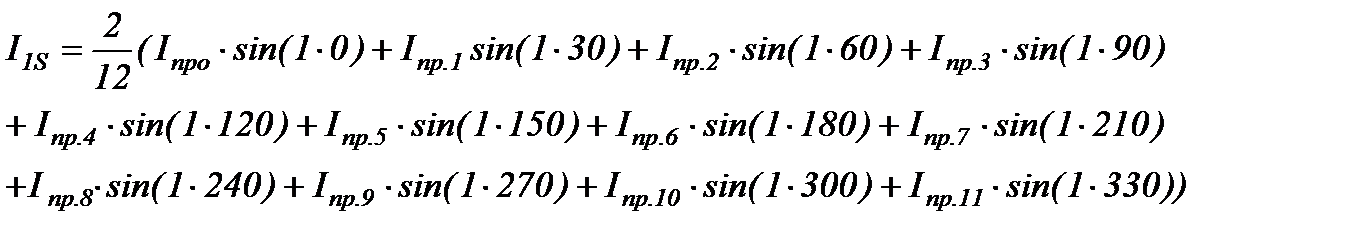
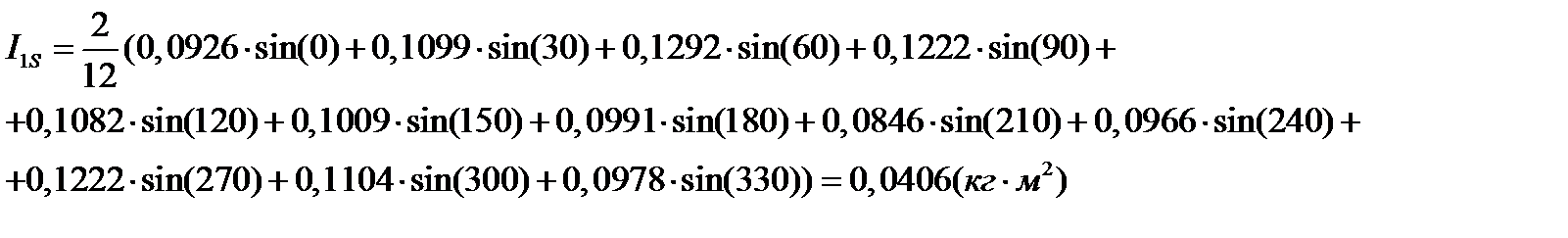
коэффициент при косинусах n-ой гармоники :
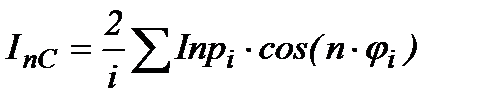 (2.10)
(2.10)
для n=1 получим
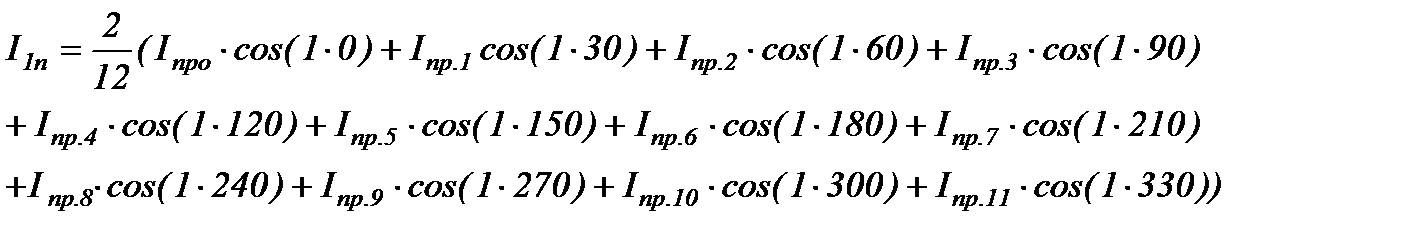
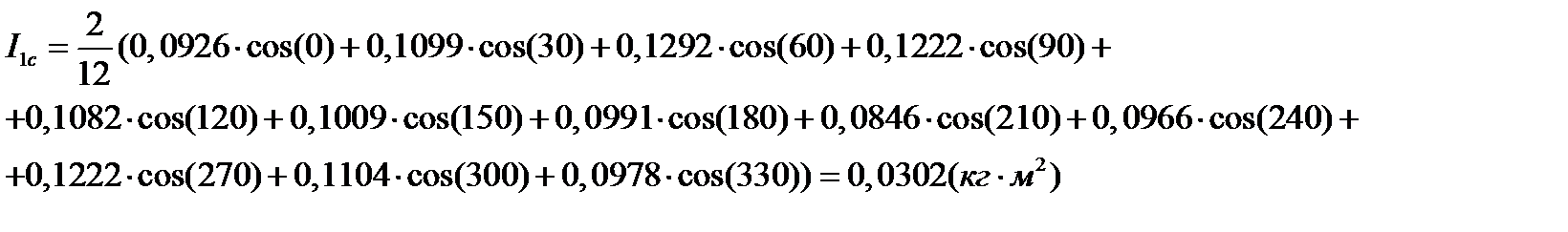
Аналогично определяем коэффициенты для n=2.3 полученные значения сводим в таблицу 2.3
Таблица 2.3 Значения коэффициентов ряда Фурье
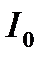 кг·м2 кг·м2 | 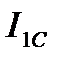 кг·м2 кг·м2 | 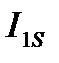 кг·м2 кг·м2 | 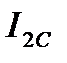 кг·м2 кг·м2 | 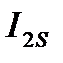 кг·м2 кг·м2 | 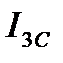 кг·м2 кг·м2 | 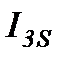 кг·м2 кг·м2 |
| 1,2737 | 0,0302 | 0,0406 | -0,078 | 0,0026 | -0,041 | 0,0284 |
Определим значение приведенного момента инерции по ряду Фурье для 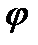 =00
=00
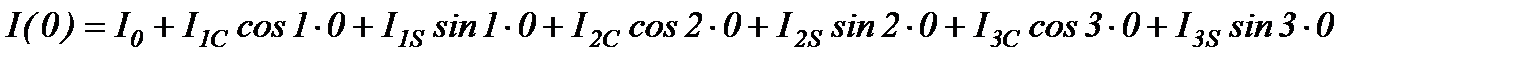 =
=
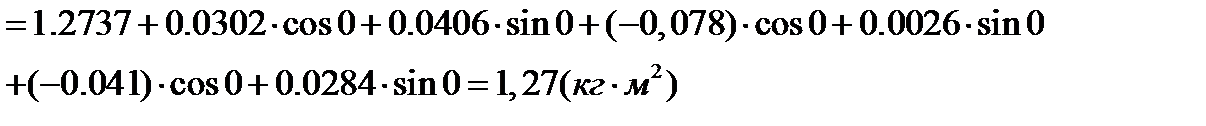
Расчет приведенного момента инерции I(φ) по формуле 2.7 представим в виде таблицы 2.4.
Таблица 2.4 Расчет момента инерции I(φ)
Угол поворота кривошипа 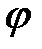 | 0° | 30° | 60° | 90° | 120° | 150° | 180° | 210° | 240° | 270° | 300° | 330° |
| I(φ) кг м2 | 0.0912 | 0.1124 | 0.1283 | 0.1212 | 0.1087 | 0.1029 | 0.0949 | 0.0875 | 0.0978 | 0.1171 | 0.1158 | 0.0954 |
| Iпр кг м2 | 0,0926 | 0,1099 | 0,1292 | 0,1222 | 0,1082 | 0,1009 | 0,0991 | 0,0846 | 0,0966 | 0,1222 | 0,1104 | 0,0978 |
По полученным данным на листе 2 строим график изменения момента инерции динамической модели I(φ)= f(φ). в масштабе μI =0,0002 кг·м2/мм
