Деформации при действии собственного веса.
При определении влияния собственного веса на деформацию при растяжении и сжатии стержней придется учесть, что относительное удлинение различных участков стержня будет переменным, как и напряжение  . Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка стержня длиной
. Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка стержня длиной 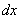 , находящегося на расстоянии
, находящегося на расстоянии 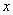 от конца стержня (Рис.4).
от конца стержня (Рис.4).

Рис.4. Расчетная модель бруса с учетом собственного веса.
Абсолютное удлинение этого участка равно

Полное удлинение стержня  равно:
равно:

Величина  представляет собой полный вес стержня. Таким образом, для вычисления удлинения от действия груза и собственного веса можно воспользоваться прежней формулой:
представляет собой полный вес стержня. Таким образом, для вычисления удлинения от действия груза и собственного веса можно воспользоваться прежней формулой:

подразумевая под S внешнюю силу и половину собственного веса стержня.
Что же касается деформаций стержней равного сопротивления, то, так как нормальные напряжения во всех сечениях одинаковы и равны допускаемым 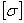 , относительное удлинение по всей длине стержня одинаково и равно
, относительное удлинение по всей длине стержня одинаково и равно

Абсолютное же удлинение при длине стержня l равно:

где обозначения соответствуют приведенным на рис.1.
Деформацию ступенчатых стержней следует определять по частям, выполняя подсчеты по отдельным призматическим участкам. При определении деформации каждого участка учитывается не только его собственный вес, но и вес тех участков, которые влияют на его деформацию, добавляясь к внешней силе. Полная деформация получится суммированием деформаций отдельных участков.
Лекция № 15. Расчет гибких нитей.
В технике встречается еще один вид растянутых элементов, при определении прочности которых важное значение имеет собственный вес. Это — так называемые гибкие нити. Таким термином обозначаются гибкие элементы в линиях электропередач, в канатных дорогах, в висячих мостах и других сооружениях.
Пусть (Рис.1) имеется гибкая нить постоянного сечения, нагруженная собственным весом и подвешенная в двух точках, находящихся на разных уровнях. Под действием собственного веса нить провисает по некоторой кривой АОВ.
Горизонтальная проекция расстояния между опорами (точками ее закрепления), обозначаемая 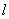 , носит название пролета.
, носит название пролета.
Нить имеет постоянное сечение, следовательно, вес ее распределен равномерно по ее длине. Обычно провисание нити невелико по сравнению с ее пролетом, и длина кривой АОВ мало отличается (не более чем на 10%) от длины хорды АВ. В этом случае с достаточной степенью точности можно считать, что вес нити равно- мерно распределен не по ее длине, а по длине ее проекции на горизонтальную ось, т. е. вдоль пролета l.

Рис.1. Расчетная схема гибкой нити.
Эту категорию гибких нитей мы и рассмотрим. Примем, что интенсивность нагрузки, равномерно распределенной по пролету нити, равна q. Эта нагрузка, имеющая размерность сила/длина, может быть не только собственным весом нити, приходящимся на единицу длины пролета, но и весом льда или любой другой нагрузкой, также равномерно распределенной. Сделанное допущение о законе распределения нагрузки значительно облегчает расчет, но делает его вместе с тем приближенным; если при точном решении (нагрузка распределена вдоль кривой) кривой провисания будет цепная линия, то в приближенном решении кривая провисания оказывается квадратной параболой.
Начало координат выберем в самой низшей точке провисания нити О, положение которой, нам пока неизвестное, очевидно, зависит от величины нагрузки q, от соотношения между длиной нити по кривой и длиной пролета, а также от относительного положения опорных точек. В точке О касательная к кривой провисания нити, очевидно, горизонтальна. По этой касательной направим вправо ось 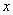 .
.
Вырежем двумя сечениями — в начале координат и на расстоянии 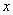 от начала координат (сечение m — n) — часть длины нити. Так как нить предположена гибкой, т. е. способной сопротивляться лишь растяжению, то действие отброшенной части на оставшуюся возможно только в виде силы, направленной по касательной к кривой провисания нити в месте разреза; иное направление этой силы невозможно.
от начала координат (сечение m — n) — часть длины нити. Так как нить предположена гибкой, т. е. способной сопротивляться лишь растяжению, то действие отброшенной части на оставшуюся возможно только в виде силы, направленной по касательной к кривой провисания нити в месте разреза; иное направление этой силы невозможно.
На рис.2 представлена вырезанная часть нити с действующими на нее силами. Равномерно распределенная нагрузка интенсивностью q направлена вертикально вниз. Воздействие левой отброшенной части (горизонтальная сила Н) направлено, ввиду того, что нить работает на растяжение, влево. Действие правой отброшенной части, сила Т, направлено вправо по касательной к кривой провисания нити в этой точке.
Cоставим уравнение равновесия вырезанного участка нити. Возьмем сумму моментов всех сил относительно точки приложения силы Т и приравняем ее нулю. При этом учтем, опираясь на приведенное в начале допущение, что равнодействующая распределенной нагрузки интенсивностью q будет  , и что она приложена посредине отрезка
, и что она приложена посредине отрезка 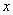 . Тогда
. Тогда

Рис.2. Фрагмент вырезанной части гибкой нити
 ,
,
откуда
 | (1) |
Отсюда следует, что кривая провисания нити является параболой. Когда обе точки подвеса нити находятся на одном уровне, то  Величина
Величина  в данном случае будет так называемой стрелой провисания. Ее легко определить. Так как в этом случае, ввиду симметрии, низшая точка нити находится посредине пролита, то
в данном случае будет так называемой стрелой провисания. Ее легко определить. Так как в этом случае, ввиду симметрии, низшая точка нити находится посредине пролита, то  ; подставляя в уравнение (1) значения
; подставляя в уравнение (1) значения  и
и  получаем:
получаем:
 | (2) |
Из этой формулы находим величину силы Н:
 | (3) |
Величина Н называется горизонтальным натяжением нити.
Таким образом, если известны нагрузка q и натяжение H, то по формуле (2) найдем стрелу провисания  . При заданных
. При заданных  и
и  натяжение Н определяется формулой (3). Связь этих величин с длиной
натяжение Н определяется формулой (3). Связь этих величин с длиной  нити по кривой провисания устанавливается при помощи известной из математики приближенной формулы)
нити по кривой провисания устанавливается при помощи известной из математики приближенной формулы)

Составим еще одно условие равновесия вырезанной части нити, а именно, приравняем нулю сумму проекций всех сил на ось 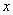 :
:

Из этого уравнения найдем силу Т — натяжение в произвольной точке

Откуда следует, что сила Т увеличивается от низшей точки нити к опорам и будет наибольшей в точках подвеса — там, где касательная к кривой провисания нити составляет наибольший угол с горизонталью. При малом провисании нити этот угол не достигает больших значений, поэтому с достаточной для практики степенью точности можно считать, что усилие в нити постоянно и равно ее натяжению Н. На эту величину обычно и ведется расчет прочности нити. Если все же требуется вести расчет на наибольшую силу у точек подвеса, то для симметричной нити ее величину определим следующим путем. Вертикальные составляющие реакций опор равны между собой и равны половине суммарной нагрузки на нить, т. е.  . Горизонтальные составляющие равны силе Н, определяемой по формуле (3). Полные реакции опор получатся как геометрические суммы этих составляющих:
. Горизонтальные составляющие равны силе Н, определяемой по формуле (3). Полные реакции опор получатся как геометрические суммы этих составляющих:

Условие прочности для гибкой нити, если через F обозначена площадь сечения, имеет вид:

Заменив натяжение Н его значением по формуле (3), получим:

Из этой формулы при заданных 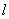 ,
,  ,
, 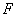 и
и 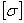 можно определить необходимую стрелу провисания
можно определить необходимую стрелу провисания  . Решение при этом упростится, если в
. Решение при этом упростится, если в  включен лишь собственный вес; тогда
включен лишь собственный вес; тогда  , где
, где 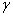 — вес единицы объема материала нити, и
— вес единицы объема материала нити, и

т. е. величина F не войдет в расчет.
Если точки подвеса нити находятся на разных уровнях, то, подставляя в уравнение (1) значения  и
и  , находим
, находим  и
и  :
:


Отсюда из второго выражения определяем натяжение

а деля первое на второе, находим:
 или
или 
Имея в виду, что  , получаем:
, получаем:
 или
или 
Подставив это значение  в формулу определенного натяжения Н, окончательно определяем:
в формулу определенного натяжения Н, окончательно определяем:
 | (6.15) |
Два знака в знаменателе указывают на то, что могут быть две основные формы провисания нити. Первая форма при меньшем значении Н (знак плюс перед вторым корнем) дает нам вершину параболы между опорами нити. При большем натяжении Н (знак минус перед вторым корнем) вершина параболы расположится левее опоры А (Рис.1). Получаем вторую форму кривой. Возможна и третья (промежуточная между двумя основными) форма провисания, соответствующая условию  ; тогда начало координат
; тогда начало координат  совмещается с точкой А. Та или иная форма будет получена в зависимости от соотношений между длиной нити по кривой провисания АОВ (Рис.1) и длиной хорды АВ.
совмещается с точкой А. Та или иная форма будет получена в зависимости от соотношений между длиной нити по кривой провисания АОВ (Рис.1) и длиной хорды АВ.
Если при подвеске нити на разных уровнях неизвестны стрелы провисания  и
и  , но известно натяжение Н, то легко получить значения расстояний а и b и стрел провисания
, но известно натяжение Н, то легко получить значения расстояний а и b и стрел провисания  , и
, и  . Разность h уровней подвески равна:
. Разность h уровней подвески равна:

Подставим в это выражение значения  и
и  , и преобразуем его, имея в виду, что
, и преобразуем его, имея в виду, что  :
:

откуда

а так как  то
то
 и
и 
Следует иметь в виду, что при  будет иметь место первая форма провисания нити, при
будет иметь место первая форма провисания нити, при  — вторая форма провисания и при
— вторая форма провисания и при  — третья форма. Подставляя значения
— третья форма. Подставляя значения 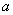 и
и  в выражения для стрел провисания
в выражения для стрел провисания  и
и  , получаем величины
, получаем величины  и
и  :
:


Теперь выясним, что произойдет с симметричной нитью, перекрывающей пролет 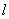 , если после подвешивания ее при температуре
, если после подвешивания ее при температуре  и интенсивности нагрузки
и интенсивности нагрузки  температура нити повысится до
температура нити повысится до  а нагрузка увеличится до интенсивности
а нагрузка увеличится до интенсивности 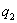 (например, из-за ее обледенения). При этом предположим, что в первом состоянии задано или натяжение
(например, из-за ее обледенения). При этом предположим, что в первом состоянии задано или натяжение  , или стрела провисания
, или стрела провисания  (Зная одну из этих двух величин, всегда можно определить другую.)
(Зная одну из этих двух величин, всегда можно определить другую.)
При подсчете деформации нити, являющейся по сравнению с длиной нити малой величиной, сделаем два допущения: длина нити 'равна ее пролету, а натяжение постоянно и равно Н. При пологих нитях эти допущения дают небольшую погрешность.
В таком случае удлинение нити, вызванное увеличением температуры, будет равно

где 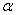 — коэффициент линейного температурного расширения материала нити.
— коэффициент линейного температурного расширения материала нити.
При повышении температуры нить удлиняется. В связи с этим увеличится ее стрела провисания и, как следствие, уменьшится ее натяжение. С другой стороны, из-за увеличения нагрузки, как видно из формулы (3), натяжение увеличится. Допустим, что окончательно натяжение увеличивается. Тогда удлинение нити, вызванное увеличением натяжения, будет, согласно закону Гука, равно:

Если  окажется меньше, чем
окажется меньше, чем  то величина
то величина  будет отрицательной. При понижении температуры будет отрицательной величина
будет отрицательной. При понижении температуры будет отрицательной величина  .
.
Таким образом, длина нити во втором ее состоянии будет равна длине при первом ее состоянии с добавлением тех деформаций, которые произойдут от повышения температуры и натяжения:

Изменение длины нити вызовет изменение и ее стрелы провисания. Вместо  , она станет
, она станет  .
.
Теперь заменим в последнем уравнении  и
и  их известными выражениями, а деформации
их известными выражениями, а деформации  и
и  — также их полученными ранее значениями. Тогда уравнение для S2 примет следующий вид:
— также их полученными ранее значениями. Тогда уравнение для S2 примет следующий вид:

В этом уравнении заменим  и
и  их значениями по формуле (2):
их значениями по формуле (2):
 и
и 
Тогда, после некоторых преобразований, уравнение для расчета натяжения может быть написано в виде:

Определив из этого уравнения натяжение  , можно найти по формуле (2) и стрелу
, можно найти по формуле (2) и стрелу  .
.
В случае, если при переходе от первого ко второму состоянию нагрузка не изменяется, а изменяется лишь температура, то в последнем уравнении интенсивность 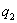 заменяется на
заменяется на 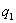 . В случае, если при переходе от первого ко второму состоянию не изменяется температура, а изменяется лишь нагрузка, то в этом уравнении средний член в квадратной скобке равен нулю. Полученное уравнение пригодно, конечно, и при понижении температуры и уменьшении нагрузки.
. В случае, если при переходе от первого ко второму состоянию не изменяется температура, а изменяется лишь нагрузка, то в этом уравнении средний член в квадратной скобке равен нулю. Полученное уравнение пригодно, конечно, и при понижении температуры и уменьшении нагрузки.
В тех случаях, когда стрела провисания не является малой по сравнению с пролетом, выведенные выше формулы, строго говоря, неприменимы, так как действительная кривая провисания нити, цепная линия, будет уже значительно отличаться от параболы, полученной нами благодаря предположению о равномерном распределении нагрузки по пролету нити, а не по ее длине, как то имеет место в действительности.
Точные подсчеты показывают, что значение погрешности в величине натяжения Н, вызванной этим предположением, таково: при отношении  погрешность не превосходит 0,3%, при
погрешность не превосходит 0,3%, при  ошибка составляет уже 1,3%, а при
ошибка составляет уже 1,3%, а при  погрешность несколько, превосходит 5%.
погрешность несколько, превосходит 5%.
Лекция № 16. Геометрические характеристики плоских сечений.
