Под алгоритмом будем понимать последовательность правил, строго следуя которым можно решить ту или иную задачу.

Задача будет считаться решенной, если для ее решения установлен определенный алгоритм.

Алгоритм Евклида служит для отыскания наибольшего общего делителя двух чисел способом последовательного деления.

Пусть a и b - натуральные числа, причем a > b и a не делится на b.

Допустим, что:

1) ,

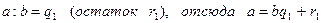2) ,

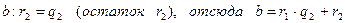3) ,

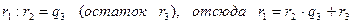4) ,

…………………………………………………………………….

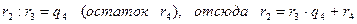n) ,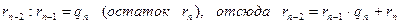

n + 1) .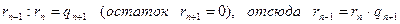

Ряд равенств:

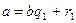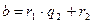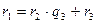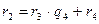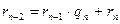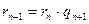, , , , …, , , выражающих зависимость между делимым, делителем, частным и остатком при последовательном делении большего числа на меньшее, меньшего на первый остаток, первого остатка на второй остаток и т. д., известен под названием алгоритма Евклида.

Рассматриваемый ряд равенств конечен. В самом деле, по смыслу деления ряд остатков (следовательно, и ряд делителей) 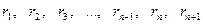есть ряд убывающих целых чисел, который обязательно должен закончиться некоторым остатком 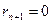, вследствие того, что число возможных остатков конечно, так как оно не может быть больше числа b. Итак, каковы бы ни были числа a и b, в результате последовательного деления большего числа на меньшее, меньшего на первый остаток, первого остатка на второй остаток и т. д., мы обязательно получим некоторый остаток 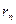, на который предыдущий остаток 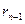разделится без остатка, и, следовательно, число 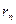будет последним, не равным нулю остатком, а значит, т последним делителем. Таким образом, возможность дальнейшего деления отпадает.

Пример. Найти НОД чисел 852 и 192.

Решение

1. Делим большее число на меньшее:

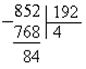
2. Делим делитель 192 на остаток 84:

3. Новый делитель делим на полученный остаток:

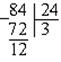
4. Снова делитель делим на остаток:

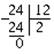
В остатке получился нуль, значит процесс деления следует прекратить. Последний делитель (12) и будет наибольшим общим делителем чисел 852 и 192.

Ответ: НОД (852, 192) = 12

Правило для нахождения НОД двух чисел способом последовательного деления.

Теорема. Чтобы найти НОД двух чисел способом последовательного деления, надо большее из данных чисел разделить на меньшее, затем, меньшее - на первый остаток, первый остаток - на второй, второй - на третий и т. д. до тех пор, пока не получится в остатке 0. Тогда последний делитель (иначе, последний не равный нулю остаток) будет наибольшим общим делителем данных чисел.

Евклид применял свой алгоритм не только в арифметике, но и в геометрии для отыскания общей меры двух отрезков путем последовательного наложения.

Основные свойства НОД

Теорема 1. На всякое число, на которое делятся без остатка два данных числа, делится и их наибольший общий делитель.

Пример. НОД (3540; 450) = 30. Кроме того, данные числа 3540 и 450 имеют общие делители 1. 2, 3, 5, 6, 10, 15.

Очевидно, что на каждый из этих общих делителей делится без остатка НОД чисел 3540 и 450, т. е. число 30.

Теорема 2. Всякое число, на которое делится без остатка наибольший общий делитель двух данных чисел, есть общий делитель этих чисел.

Пример. НОД (3540; 450) = 30. Делителями 30 являются числа: 1. 2, 3, 5, 6, 10, 15. Очевидно, что на каждое из этих чисел делятся 3540 и 450.

Теорема 3. Если каждое из двух данных чисел a и b умножить на какое-либо натуральное число m, то и наибольший общий делитель данных чисел умножится на то же число m.

Пример. НОД (558; 540) = 18. Умножив каждое из данных чисел на 2, будем иметь: НОД ( 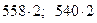) = 36.