Тема: Повне дослідження функції та побудова їі графіка.

Індивідуальне завдання № 2.2.1

Методичні вказівки

З вищої математики

Тема: Диференціювання.

Викладачі : доцент Воробйова А.І.

Тема: Повне дослідження функції та побудова їі графіка.

а) Основні теоретичні відомості.

Під повним дослідженням функції розуміють дослідження за такою схемою (водночас дамо деякі рекомендації щодо побудови графіка функції):

1. Визначити область існування функції. Це дає змогу визначити ті точки осі абсцис, над якими пройде графік.

2. Дослідити функцію на періодичність. Якщо функція буде періодичною з періодом Т, то подальше дослідження проводити лише на відрізку довжини Т.

3. Дослідити функцію на парність. Якщо функція буде парною або непарною, то подальше дослідження проводити лише на області визначення, що лежить на невід’ємній півосі дійсної осі.

4. Дослідити функцію на неперервність, встановити вид точок розриву та знайти границю функції на кінцях проміжків області визначення.

Знайти вертикальні j похилі асимптоти та побудувати їх.

6. Знайти інтервали монотонності і точки екстремуму функції. Знайти значення функції в цих точках та побудувати відповідні точки графіка.

7. Знайти інтервали опуклості, угнутості і точки перегину графіка функції.

Побудувати одержані точки.

8. Знайти точки перетину графіка функції з осями координат та побудувати їх.

9. При необхідності побудувати декілька контрольних точок.

10. Графік будуємо паралельно повному дослідженню функції.

б) Методичні рекомендації" для повного дослідження функції та побудови графіка функції:

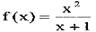Виконати повне дослідження функції та побудувати їі графік.

Розв'язання. 1) Функція визначена на всій числовій осі, крім точки де х+1=0, тобто х= -1. Отже, область визначення: D(f)=(-∞;-1)∪(-1 ;+ ∞).

2) Ця функція не є періодичною як дробово-раціональна (наприклад, точка розриву х = -1 не повторюється).

З) Функція не відноситься ні до парних, ні до непарних, бо область визначення не є симетричною відносно початку координат (х = 1 є D(f) , а x=-1 ∉ D(f)).

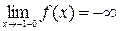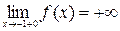4) f(х) є часткою двох функцій х2 і х+1 неперервних на всій числовій осі, тому вона буде неперервною на всій числовій осі, крім точки х = - 1, в якій х+ 1=0. Отже f (х) неперервна на всій D(f). Так як , а l, то х = -1 - точка розриву другого роду.

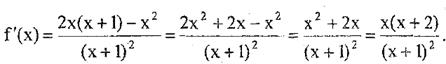5) Знайдемо f '(х):

f '(х) = 0 при х1 = -2 і х2 = 0. Точок, де f ' (х) не існує в області визначення немає.

Побудуємо таблицю:

інтервали знакосталості f '(х)	(-∞;-2)	х=-2	(-2;-1)	(-1;0)	х=О	(0;+ ∞)
знак f '(х)	+		-	-		+
поведінка f (х)	Ö	х = - 2 точка max y(-2)=-4	Ø	Ø	x = 0 точка min у(0)=0	Ö

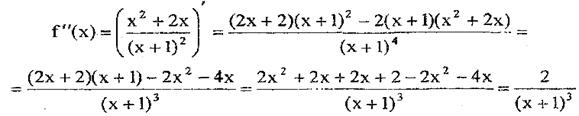6) Знайдемо f"(х):

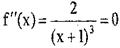
Точок, де , немає. Отже, графік функції точок перегину немає.

f "(х) > 0 на інтервалі (-1;+ ∞), тому на цьому інтервалі графік функції угнутий ( ) . f "(х) < 0 на інтервалі (-∞;-1), тому на цьому інтервалі графік функції опуклий (∩).

7) Пряма х = -1 є вертикальною асимптотою графіка функції, бо 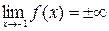. Похилі асимптоти

мають вигляд y=kx+b, де 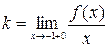, а

.

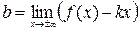Так як

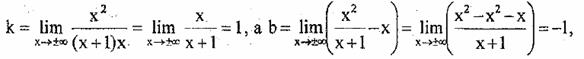
то пряма у = х- l є асимптотою графіка функції.

8) Точки перетину графіка з віссю ОХ є розв'язком системи

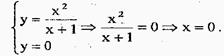Отже, точка (0;0) є точкою перетину графіка з віссю ОХ. Точки перетину графіка з віссю ОУ є розв'язком системи

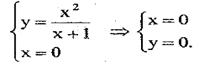Маємо точку (0;0). Отже, графік функції перетинає вісь ОУ в точці (0;0).

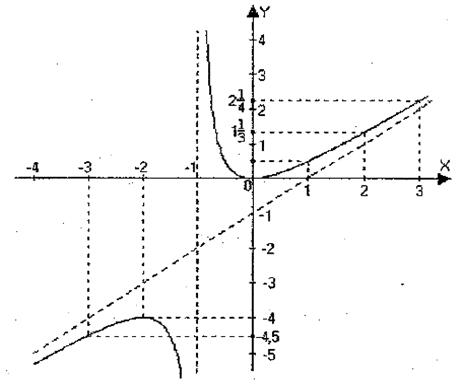
9) Надаючи аргументу х декілька значень і знайшовши відповідні значення функції, ми одержимо декілька точок, через які проходить графік.

х	- 3	- 1/2
у	- 4,5	1/2	1/2	4/3	9/4