Жалғыздық теоремасы

Жүйелілік критерийі

Алдыңғы тақырыпта біз дифференциалдау мен регулярлық ұғымдарының эквиваленттілігін дәлелдедік. Бұл бізге нақты функциялардың регулярлығын тексеруге ыңғайлы қарапайым регулярлық белгілердің қатарын бірден береді. Нақты:

ζ нүктесінде жүйелі функциялардың ақырғы мәндерінің қосындысы мен туындылары ζ нүктесінде тұрақты болады.

ζ нүктесінде тұрақты екі функциялардың да қатынасы да функция болып табылады.

Егер f(z) ζ нүктесінде тұрақты болса, ал F(ω) функциясы f(ζ) нүктесінде тұрақты болса, онда φ(z) F( f(z)) ζ нүктесінде тұрақты.

Біз қазір одан да тереңірек нәтижелерді көрсетеміз. Негізгі болып Морер теоремасы деп аталатын критерий табылады.

Теорема 4.1. f(z) функциясы D облысында үзіліссіз және f(z) интегралы D-да жатқан кез келген тұйық сынығы нөлге тең. Сонда f(z) D облысында үзіліссіз болады.

Дәлелдеу. G арқылы D облысының кез келген бір байланысты бөлігін белгілейміз.

І тараудың 5.2 теоремасының көмегімен f(z) функциясының интегралы кез келген түзелетін тұйық қисық бойынша (D облысында жатқан) нөлге тең екеніне көз жеткіземіз. Осыдан біз f(z) функциясының интегралы D облысында жатқан кез келген түзелетін қисық бойынша сол қисықтың тек бастапқы және ақырғы нүктелеріне тәуелді екенін шығарамыз. Осы деректен біз 3,4 теоремадағыдай f(z) функциясының F(z) бірінші түрленуі (интегралдың жолдан тәуелділігін есепке ала тұрып) D облысында тұрақты. 3.3 теоремаға сәйкес n=1 бұл D облысында f(z)=F(z) функциясы да тұрақты екенін білдіреді. G – D - ның кез келген бір байланысты бөлігі болғандықтан, теорема дәлелденді.

Морер теоремасының көмегімен келесі белгілер дәлелденеді.

Теорема 4.2. Егер f(z, ω) G облысында z бойынша кез келген ω 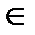Е тұрақты болса және

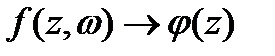
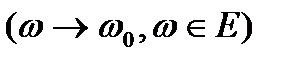
G кез келген тұйық бөлігінде z бойынша тең, онда φ(z) G облысында да үздіксіз.

Дәлелдеуі. f(z, ω) функциясы G облысында z бойынша үздіксіз, ал яғни І тараудың теорема 4.1. бойынша φ(z) функциясы G облысының кез келген тұйық бөлігінде үзіліссіз. Содан байқасақ, І тараудың 6.1 теоремасындағы интегралдау ретінің ауысу мүмкіндігі мен шекке бірқалыпты өту күшіне қарай аламыз.

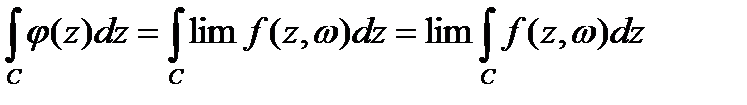
Мұнда C - G-да жататын еркін контур. Егер біз С ретінде G–да жатқан кез келген облыстың шекарасын алатын болсақ, онда соңғы интеграл Коши теоремасы бойынша нөлге тең болады.

Осылайша, 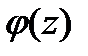функциясы G облысында үзіліссіз және 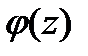-тан G интегралында жатқан кез келген облыстың шекарасы бойынша (шекарасымен бірге) нөлге тең. Морер теоремасы бойынша 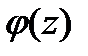функциясы G облысында тұрақты. Теорема дәлелденді.

4.2 теоремасының көп тараған жеке жағдайлары ретінде келесі пайымдаулар табылады:

Салдар 1. Регулярлы функциялардың бірқалыпты жинақталатын қатарларының қосындысы сол жиынның қатар бірқалыпты жинақталатын барлық ішкі нүктелерінде тұрақты функция болып табылады.

1 салдардың ерекше жағдайын белгілеп өтейік:

Салдар 2. Дәрежелі қатардың қосындысы оның жинақталу шеңберінің ішінде тұрақты.

Келесі белгі де үлкен мәнге ие.

4.3 теорема. L - 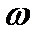жазықтығындағы қандай да бір түзелетін контур, ал 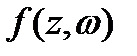- z бойынша G облысында кез келген 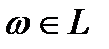тұрақты және 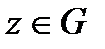, 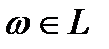кезінде айнымалылардың жиынтығы бойынша үзіліссіз функция. Онда функция

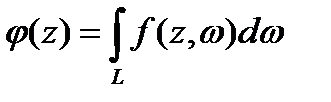
G облысында тұрақты.

Дәлелдеуі. G облысында өзінің С шекарасымен бірге D облысын алайық. І тараудың 6.2 теоремасы бойынша 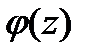функциясы G облысында үзіліссіз және

.

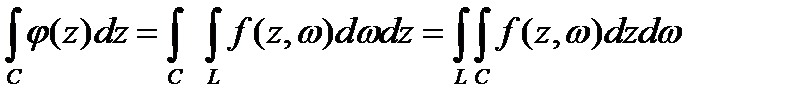Коши теоремасы бойынша ішкі интеграл нөлге тең. Осылайша 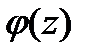функциясы Морер теоремасының шарттарын қанағаттандырады. Демек, 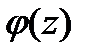- G облысында тұрақты функция және теорема дәлелденді.

Ескерту. 4.2 мен 4.3 теоремаларын біріктіре отырып, 4.3 теорема 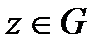бойынша бірқалыпты жинақталатын болса, өзіндік емес интеграл үшін де өз күшінде қалады.

4.3 теореманың бір жеке жағдайын белгілеп кетейік.

Салдар 1. Егер f(ω) функциясы L контурында үзілессіз болса, онда функция

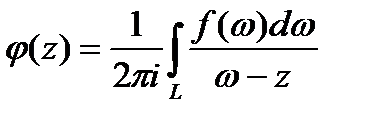
L нүктелері жоқ контурының кез келген облысында тұрақты.

Шынында, L нүктелері жоқ контурының D кез келген облысында, 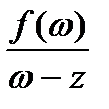функциясы кез келген 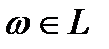кезінде z бойынша тұрақты және 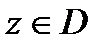, 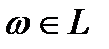кезінде айнымалылардың жиынтығы бойынша үзіліссіз. Сондықтан біздің пайымдау 4.3 теоремадан шығады.

Басқа түрдегі бір нәтиже келтірейік.

4.4 теорема. Егер f(z, ω) кез келген 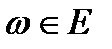кезінде G облысында z бойынша тұрақты болса және

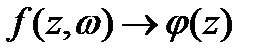
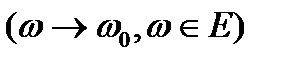
G облысының тұйық бөлігінде z бойынша бірқалыпты болса, онда

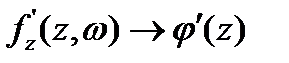
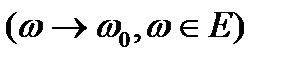
G облысының тұйық бөлігінде z бойынша бірқалыпты.

Дәлелдеуі. В арқылы G кез келген тұйық бөлігін белгілейік, ал D арқылы В бар, бірақ өзінің С шекарасымен бірге G-да жатқан облысты белгілейміз. Сонда 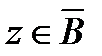, 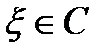кезінде

,

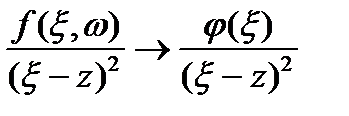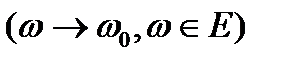
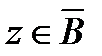мен 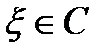бойынша бірқалыпты. І тараудың 6.1 теоремасының интегралдау ретінің өзгерту мүмкіндігі мен бірқалыпты шектік өту күшіне қарай мынаны аламыз

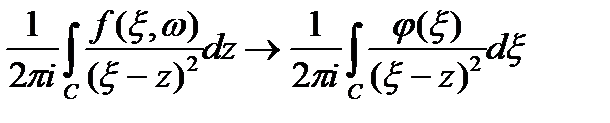
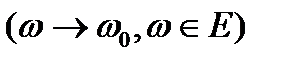
3.3 теоремаға сәйкес сол жағы 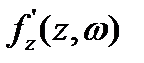тең, ал оң жағы 4.2 мен 3.3 сәйкес 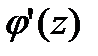тең. Осыдан теореманың пайымдауын аламыз.

Салдар 1. G облысының кез келген тұйық бөлігінде бірқалыпты жинақталатын тұрақты функциялар қатарын бөлшектеп дифференциалдап алуға болады және дифференциалдаудан кейінгі алынған қатар G облысының кез келген тұйық бөлігінде бірқалыпты жинақталатын болады.

Келесі нәтиже 4.4 теоремаға ұқсас дәлелденеді.

4.5 теорема. Егер f(z, ω) функциясы кез келген 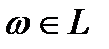кезінде G облысында z бойынша тұрақты болса және 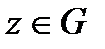, 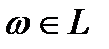кезінде айнымалылардың жиынтығы бойынша үзіліссіз, ал

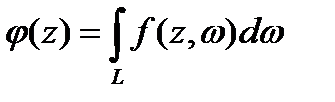
онда

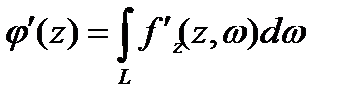
Ескерту. 4.5 теореманың пайымдауы бірқалыпты жинақталатын өзіндік емес интегралдар үшін де өз күшінде.

Қорытынды ретінде тұрақты функциялардың ықшамдылық принципі атына ие тағы бір теореманы дәлелдейміз.

4.6 теорема. G облысында тұрақты 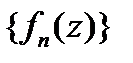функциясының бірқалыпты шектелген тізбегінен G облысының кез келген тұрақты тұйық бөлігінде бірқалыпты жинақталатын 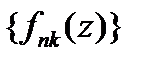бір тізбек астын белгілеп алуға болады.

Дәлелдеуі. 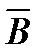деп G-дың кез келген тұйық бөлігін белгілеп алайық, ал D арқылы 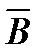-ға ие, бірақ C өз шекарасымен бірге G-да жатқан облысты белгілеп аламыз. 3.3 теоремаға сәйкес

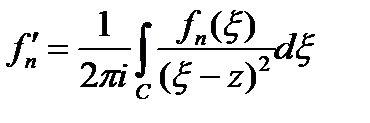
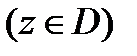
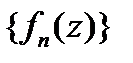тізбегінің бірқалыпты шектелуі

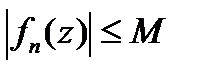
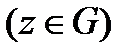
Білдіреді.

Сондықтан, интеграл модулін бағалай отырып интеграл асты функцияның модулінің максимумын интегралдау жолының ұзындығынан шығара отырып,

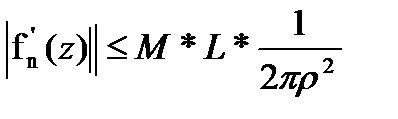
Аламыз. Мұнда L – С ұзындығы, ρ – 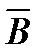-дан С-ға дейінгі ара қашықтық.

Осылайша 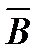жиынында 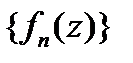функцияларының тізбегі де бірқалыпты шектелген, және олардың туындыларының да тізбегі бірқалыпты шектелген. Бірақ туындылардың тізбектілігінің бірқалыпты шектелуінен 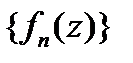тізбегінің бірдеңгейлі үзіліссіздігі болады. Сондықтан Арцел теоремасын қолдана отырып (§4, 1 тарау), 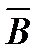жиынында бірқалыпты жинақталатын 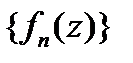тізбектің тізбек астын таңдай аламыз.

Осылай, G облысының әрбір тұйық бөлігі үшін 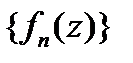тізбегінен осы бөлікте бірқалыпты жинақталатын тізбек астын бөле аламыз (жалпы айтқанда ір бөлікке өзінікін). G кез келген тұйық бөлігінде бірқалыпты жинақталатын тізбек астын бөле алатынымызды көрсетеміз. Бұл мақсат үшін қосындысы G облысын толығымен жабатын 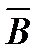жиыны үшін кеңейтілетін тізбек құраймыз. Әр 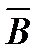жиыны үшін өз тізбегін құрамыз. Сосын бірінші функцияны бірінші тізбек астынан аламыз, екіншіні – екіншіден және т.с.с. бұл тізбек негізгі болып қабылданады.

Жалғыздық теоремасы

Қазір біз жалғыздық теоремасы деп аталатын тұрақты функциялардың маңызды қасиеттеріінің бірін дәлелдейміз.

5.1-теорема. 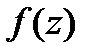функциясы D облысында тұрақты болсын ал 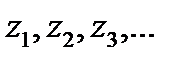Д ішіндегі шекті нүктесі бар Е шексіз нүктелер тізбегі . Егер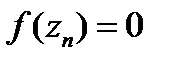 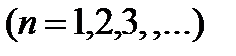болса онда функцияс Д облысы бойынша 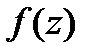функциясы 0 ге тең.

Дәлелдеуі. А- D да жатқан 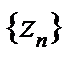тізбегінің шектік нүктесі болсын. Алдымен көрсетейік, 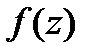функциясы а нүктесінің кейбір маңайында нөлге тең. 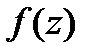функциясы а нүктесінде тұрақты екенін білеміз, яғни

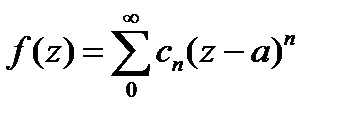
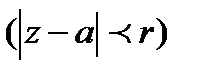
Жалпы шектеусіз 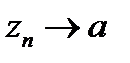екенін, және барлық n кезінде 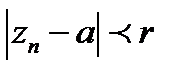ие болатынымызды есептеуге болады. 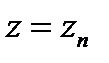деп және 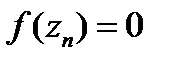еске ала отырып, аламыз

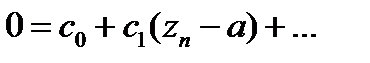
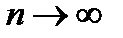кезінде шекке жете отырып, 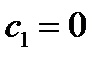екенін табамыз. Мұны қолдана отырып, жаза аламыз

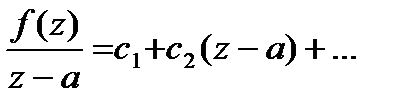
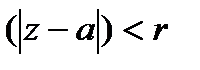
Қайтадан 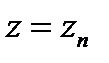, содан 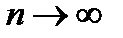деп алып, 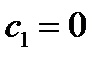екенін табамыз. Осы процессті қайталай отырып 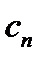нөлге тең екеніне көз жеткіземіз, яғни f(z) функциясы 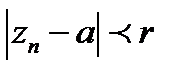кезінде нөлге тең.

f(z) функциясы Д облысының кез келген нүктесінде нөлге тең екенін көрсетейік. Бұл үшін 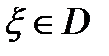кез келген нүктесін алайық және оны а нүктесімен Д-да жатқан L сынығы арқылы байланыстырайық (бұл мүмкін, себебі облыс – байланыс жиын). Енді, 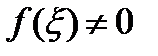деп алайық. Онда L сынығында келесі қасиеттерімен 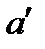табылады:

L аумағында а және 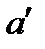нүктелері арасында f(z) функциясы нөлге тең.

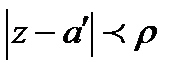шеңберінде, кез келген 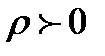кезінде, f(z) функциясында нөлден басқа ең болмағанда бір нүкте болады.

Онда біз 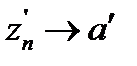және 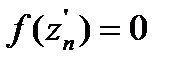бола алатын L нүктелерінің 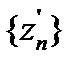тізбегін ала аламыз. Содан а нүктесінің орнына 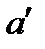нүктесін, ал 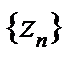тізбегінің орнына 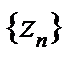тізбегін алып, жоғарыда жүргізілген ойларды қайталаймыз. Біз 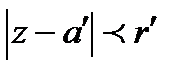кезінде 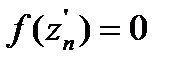аламыз. Бұл 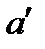нүктесінің екінші қасиетіне қайшы келеді.

Осылайша, 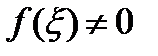болатын 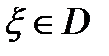нүктесі табылады деген болжам бізді қайшылыққа әкелді. Теорема дәлелденді.

Жалғыздық теоремаларын қолдануда аналитикалық жалғастыру түсінігі үлкен рөл ойнайды.

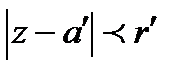
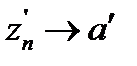
Бізге берілсін: Е жиыны , Е-ге анықталған f(z) функциясы, және Е жиынына ие D облысы. Е жиынындағы f(z)-пен сәйкес келетін D облысында тұрақты f(z) функциясын біз D облысындағы f(z) функциясының аналитикалық жалғасы деп атаймыз.

Жалғыздық теоремасынан аналитикалық жалғастыру принципі атауын алатын пайымдау жүреді: Егер Е жиыны Д облысының ішінде жататын бір шектік нүктесі бар болса, онда f(z) функциясының Д облысына бір ғана аналитикалық жалғасы болады.

Шынымен, егер f(z) функциясының Д облысынд екі түрлі аналитикалық жалғасы болса, біз жалғыздық теоремасымен қарсылыққа келер едік.

Аналитикалық жалғастыру принципі көмегімен кейбір элементар функцияларды айнымалының комплекстік мәндеріне қойып (таратып) , комплектік жазықта олардың қасиеттерін зерттеуге болады.

Талдаудан 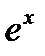, , 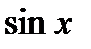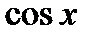функциялары барлық шынайы х үшін жиналатын дәрежелік қатарларға бөлінетіні белгілі.

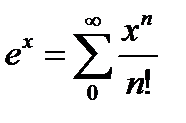
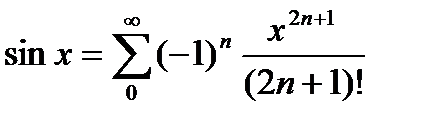
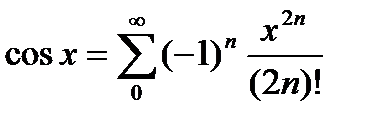
Бұл қатарлар айнымалының барлық комплекстік мәндері үшін де жиналады. Сондықтан комплекстік мәндердің z қатарлары үшін 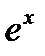, , 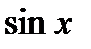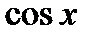функцияларын анықтау естесственно)). 4.2 теоремаың 2 салдарын сәйкес бұл қатарлардың қосындысы барлық комплекстік жазықтық бойынша функция болып табылады, яғни, барлық комплекстік жазықтыққа 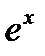, , 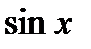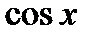функцияларының аналитикалық жалғасын береді. Аналитикалық жалғастыру принципы бойынша басқа жалғасулар болмайды.

Аналитикалық жалғастыру ретінде пайда болған комплекстік айнымалының функцияларын қалай зерттеу керегін көрсетеміз. Жеке жағдайда шынайы мәндер үшін белгілі формулалар айнымалының комплекстік мәндеріне қалай ауыстырылатынын көрсетеміз. Кез келген формула үшін пайымдаулар бірдей болғандықтан, бір формуламен шектелеміз.

Мысал 1. Кез келген комплекстік 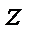пен 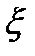үшін келесі формула

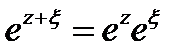
Сай.

(5.1) формуланың екі бөлігінде де кез келген бекітілген 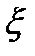кезінде z бойынша және кез келген бекітілген z кезінде 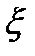бойынша тұрақты функциялар тұр. Бізге бізге осы функциялар барлық z және 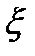кезінде сәйкес келетінін дәлеледеу керек. Алдымен 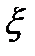шынайы мәндерін қарастырайық. Егер осы кезде z-те жарамды болса, онда формула әділетті. Жалғыздық теоремасының күшіне орай z айнымалы екі комплексті функциясының күшіне орай жазықтық бойында тұрақты және з барлық шынайы мәндеріне тепе тең келеді . Демек, (5.1) формула кез келген комплекстік z және кез келген шынайы 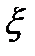кезінде дәлелденді.

.

Енді кез келген комплекстік z тіркей отырып жіне ұқсас біздің функциялармен 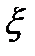функциялар сияқты ойлау жүргізе отырып (5.1) формула кез келген z және 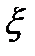кезінде әділетті екеніне көз жеткіземіз.

Әрине, (5.1) формуланы қатарларды қайта көбейтумен дәлелдеу қиын емес, бірақ келтірілген ойлау әдісі тек қарапайымдылығымен ғана емес жалпылығымен де керемет.

(5.1) формула көмегімен кез келген комплекстік z кезінде 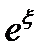функциясының мәндерін есептеу үшін қарапайым формуланы да алу оңай. Шынымен, 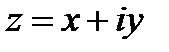қояйық. Онда (5.1) формулаға сәйкес 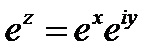ие боламыз. 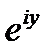есептеу үшін z орнына 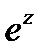Iy қоямыз және шынайы және жалған бөліктерін бөлеміз. Бұл бізге Эйлер формуласын береді

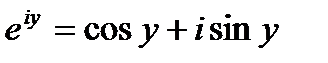
Оның көмегімен табамыз

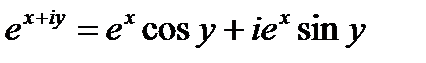
(5.2) формуладан шығады

.

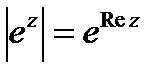Талдауда кездесетін көптеген функцияларды айнымалының комплекстік мәндеріне аналитикалық түрде жалғастыруға болады. Көрсеткіш және тригонометриялық функциялар үшін бұл тіпті оңай жасалады, ал басқалар үшін – қиын. Мысалы, lnx аналитикалық жалғасы бізге келесі тарауда айналысатын қиындық туғызады. Қазір біз айнымалының қасында емес, интегралмен шынайы мәндері үшін анықталған функцияның аналитикалық жалғасының бір мысалын қарастырамыз.

Мысал 2. Z шынайы оң үшін интегралмен анықталатын 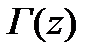Эйлер гамма-функцияларының кешендік жазықтығына аналитикалық жалғасын табамыз.

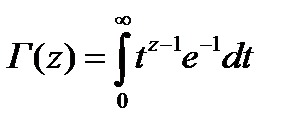
T^z-1 интеграл астын кез келген t ˃ 0 кезінде комплекстік жазықтықта толығымен аналитикалық түрде оңай жалғастыруға болады, өйткені

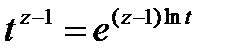
Ал көрсеткіш функцияның аналитикалық жалғастыруымен біз таныспыз. Сондықтан, 4.3 теореманы қолдана отырып, біз интеграл ды көреміз

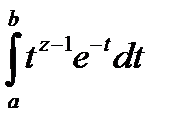
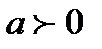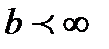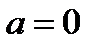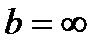және кезінде барлық комплекстік жазықтықта тұрақты болатын z функциясы болып табылады. Бірақтан және кезінде интеграл өзіндік емес болып қалады және бізге қандай z кезінде ол бірқалыпты жинақталатынын түсіндіру қажет. 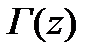анықтауыш интеграл екі ерекшелікке ие болғандықтан (нөлде және шексіздікте), оны екі интегралдардың қосындысына бөліп және олардың әр қайсысының жинақталуын жеке зерттеу керек.

Қойсақ

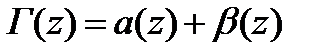
мұнда

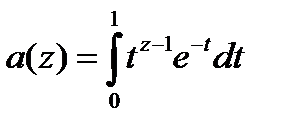
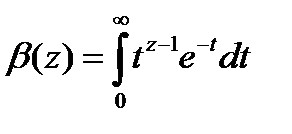
Алдымен 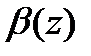интегралын зерттейік. Re 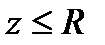кезінде (5.3) формуланың күшіне қарай интеграл асты функцияның теңсіздігін жазамыз

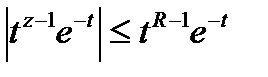
Интегралдау арасында 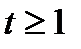және 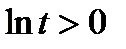болғандықтан. Бірақ

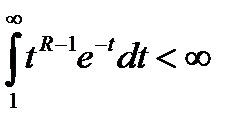
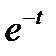функциясы 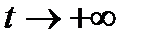кезінде t-ның кез келген дәрежесінде нөлге жылдамырақ жетеді. Сәйкесінше интегралдардың бірқалыпты жинақталу белгісі бойынша (§6 І тараудың соңы) 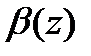функциясын анықтайтын интеграл кез келген R кезінде 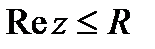жарты жазықтығында z бойынша бірқалыпты жинақталады. 4.3 теоремадағы ескертуді қолдана отырып 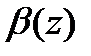функциясы комплекстік жазықтықтың бойында тұрақты екенін аламыз.

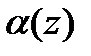арналған интегралға өтейік. 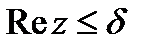кезінде интеграл асты функциясы үшін теңсіздік жаза аламыз

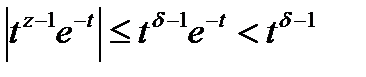
Интегралдау арасында 0<t<1 және 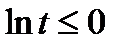болғандықтан, бірақ 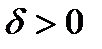кезінде аламыз