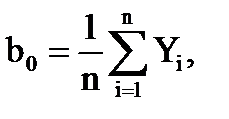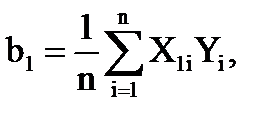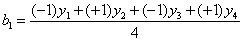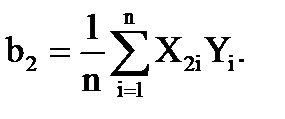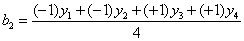Полиномиальное приближение
Рассмотрим квадратичную модель, в которой функция регрессии представляет собой полином второй степени. Уравнение регрессии квадратичной модели имеет следующий вид.
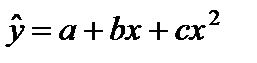
В качестве независимых переменных в уравнении используются переменные x и x2.
| № | Наименование регрессионной модели | Вид регрессионной модели | Коэффициент детерминации R2 |
Часть 2 ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
| 1. Определить реалистичное содержание целевой функции | (Целевая функция, функцию отклика, зависимая переменная, реакция системы на воздействие факторов, содержание целевой функции) Y - ________________________ | Проходка за рейс | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. Определить реалистичное содержание (сущность) факторов | (Независимые переменные, от которых зависит целевая функция) Содержание факторов X1 - ______________________________________ X2 - ______________________________________ X3 - ______________________________________ | Скорость вращения долота, Осевое усилие | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3. Определить уровни варьирования значений факторов | Минимальное значение каждого фактора Хi min = ____________ Максимальное значение каждого фактора Xi max = ____________ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4. Определить среднее значение фактора | Среднее значение фактора определяется по формуле 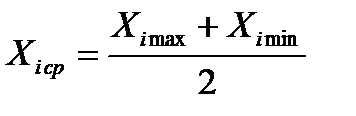 . X1ср= __________ X2ср = __________ X3ср = __________ . X1ср= __________ X2ср = __________ X3ср = __________ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. Определить интервал варьирования фактора | Интервал варьирования определяется по формуле: dxi = Xi 0 – Xi min = Xi max - Xi 0. = ___________ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. Проверить корректность определения значений факторов | Для этого необходимо составить таблицу натуральных значений факторов
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. Определить нормированные значения факторов | Нормированные значения определяются формулой 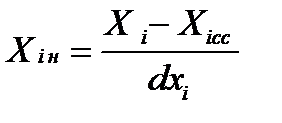 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8. Составить матрицу планирования эксперимента (полный факторный) | Полный двухфакторного эксперимента первый столбец вводится искусственным путем и постоянен и равен 1.
| В примере, показанном ниже, рассматривается только два фактора. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9. Определение необходимого числа параллельных опытов | Рекомендуется проводить по каждому опыту равномерное количество дублирующих опытов. В общем случае их должно быть не менее 3…5. Провести по 5 параллельных опытов на каждую комбинацию факторов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10. Провести факторный эксперимент | Определить численные значения функции отклика в зависимости от комбинации значений факторов и составить матрицу с результатами экспериментов
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11. Вычислить среднее значение функции отклика | 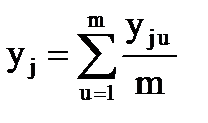 (1) при m - число повторных опытов (1) при m - число повторных опытов | Среднее значение выходной величины Yi в каждой точке определим по формуле (1) при (m = 3) Y1 = (43+35+48)/3 = 42 Y2 = (90+86+94)/3 = 90, Y3 = (10+16+16)/3 = 14, Y4 = (56+54+58)/3 = 56 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12. Вычислить дисперсию среднего арифметического для каждой строки матрицы эксперимента | 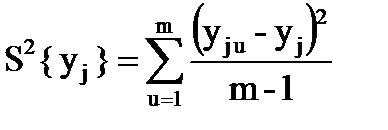 m – количество параллельных опытов в строке матриц m – количество параллельных опытов в строке матриц | Определим по формуле (2) построчную дисперсию S2{y1}= [(43–42)2 +(35–42)2 + (48–42)2]/2 = 43, S2{y2}= [(90–90)2 +(86–90)2 + (94–90)2]/2 = 16, S2{y3}= [(10–14)2 +(16–14)2 + (16–14)2]/2 = 12, S2{y4}= [(56–56)2 +(54–56)2 + (58–56)2]/2 = 4. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13. Составить таблицу расчета дисперсий |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Проверить однородность дисперсии с помощью критерия Кохрена | Критерий (коэффициент) Кохрена показывает, какую долю в общей сумме построчных дисперсий занимает максимальная из них. Определить критерий Кохрена по формуле  где smax – наибольшая величина дисперсии; si – дисперсия i-го опыта N – общее число опытов в матрице. В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N , где N – число опытов (количество строк в матрице планирования) где smax – наибольшая величина дисперсии; si – дисперсия i-го опыта N – общее число опытов в матрице. В случае идеальной однородности построчных дисперсий коэффициент Gp стремился бы к значению 1/N , где N – число опытов (количество строк в матрице планирования) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| выбрать среди всей совокупности рассчитанных построчных дисперсий число с максимальной дисперсией | S2{yi}мах | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| вычислить сумму всех построчных дисперсий | ΣS2{yi} | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| вычислить отношение максимальной дисперсии к сумме всех построчных дисперсий: | 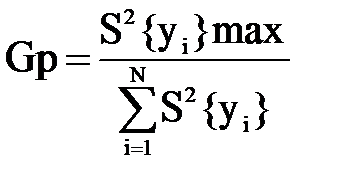 | По данным из нашего примера определим расчетное значение коэффициента Gp = 43/(43+16+12+4) = 0,57. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Задать уровень значимости | Для инженерных задач достаточен уровень значимости a = 0,05 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить степени свободы | степени свободы числителя (f1) f1= m –1 m – количество параллельных опытов в строке матриц степень свободы знаменателя (f2) f2 = N. N – общее число опытов в матрице | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Cравнить расчетное значение коэффициента Кохрена с табличным значением Найти значение f1 в горизонтальном заголовке таблицы (выбирается столбец), Найти значение f2 выбирается слева в вертикальном заголовке таблицы (выбирается строка) Установить табличное величину критерия Gт на пересечении выбранных столбца и строки | В соответствии с таблицей коэффициентов для a = 0,05; f1 = 3 – 1 = 2; f2 = 4, Gт = 0,77 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Если выполняется условие: Gp < Gт, то с достоверностью 1 – a все построчные дисперсии признаются однородными. В противном случае гипотезу отвергают. | Gт = 0,77; Gт > Gp , т.е. условие выполняется | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14. Выбрать вид уравнения регрессии (модели отклика) | Рекомендуется линейная модель Y = b0 X0 + b1 X1 + b2 X2; Y = b0 X0 + b1 X1 + b2 X2 +b12 X1Х2; (Х0 =1). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15. Вычислить коэффициенты регрессии |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16.Проверить статистическую значимость коэффициентов регрессии | Оценка производится по t-критерию Стьюдента. Т.е. проверяется отклонение от нуля найденной оценки. Для каждого коэффициента bk вычисляется коэффициент Стьюдента: 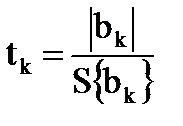 где bk – коэффициент уравнения регрессии S{bk} – оценка среднего квадратичного отклонения погрешности определения коэффициента. где bk – коэффициент уравнения регрессии S{bk} – оценка среднего квадратичного отклонения погрешности определения коэффициента. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить оценку генеральную дисперсию воспроизводимости | Оценкой дисперсии воспроизводимости S2в, характеризующая точность одного измерения, является средняя из всех построчных дисперсий 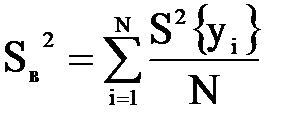 | S2в = (43 + 16 + 12 + 4)/4 = 18,75 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определитьдисперсию коэффициентов, найденных по экспериментальным данным | 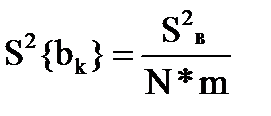 | S2{bk} = 18,75/(4*3)= 1,56 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Выполнить оценкудисперсию коэффициентов, найденных по экспериментальным данным | Оценка 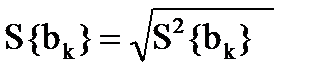 | Для рассматриваемого примера S{bk} = 1,25. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вычислить критерий Стьюдента | 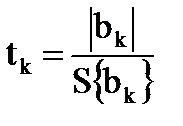 | Определим расчетные значения коэффициента Стьюдента t0 = 50,5/1,25 = 40,4; t1 = 22,5/1,25 = 18; t2 = 15,5/1,25 = 12,4; t12 = 1,5/1,25 = 1,2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Выбрать уровень статистической значимости | a = 0,05 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить число степеней свободы | f = N (m – 1) | f = 4 (3 – 1) = 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Найти табличное значение коэффициента Стьюдента | При выбранном уровне статистической значимости a по таблицам распределения Стьюдента при числе степеней свободы f = N (m – 1) находят табличное значение коэффициента tтабл. 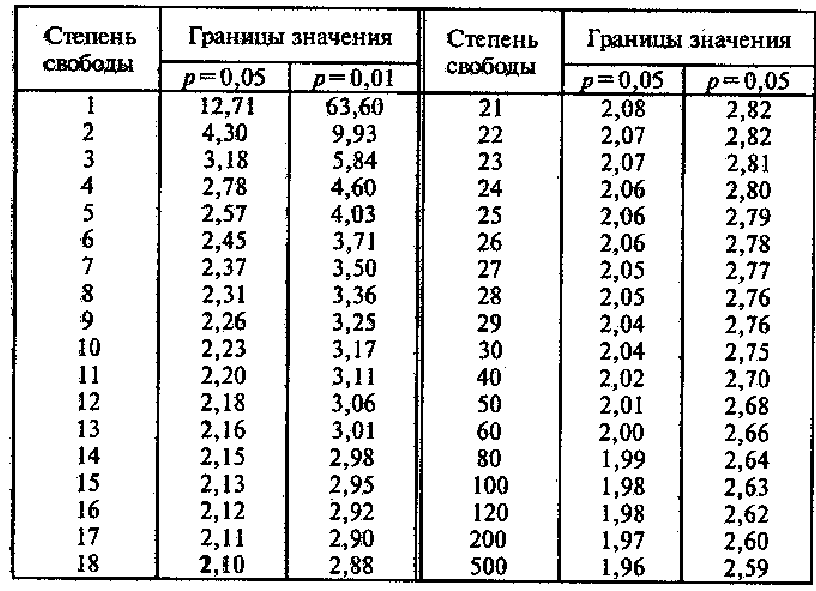 | Из таблиц при уровне статистической значимости a = 0,05 и числе степеней свободы f = 4 (3 – 1) = 8 , табличное значение коэффициента равно tт = 2,3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сравнить табличное значение с расчетным | Если выполняется неравенство tтабл > tk, то принимается нуль-гипотеза, т.е. считается, что найденный коэффициент ak является статистически незначительным и его следует исключить из уравнения регрессии. | Сопоставление расчетных значений tk с табличным tт. Неравенство выполняется для t12. Следовательно, можно предположить, что a12 статистически незначим и его можно исключить из уравнения регрессии | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Составить уравнение регрессии с учетом статистической значимости коэффициентов | Y = b0 X0н + b1 X1н + b2 X2н | Уравнение регрессии, содержащее статистически значимые коэффициенты, будет (в кодированной системе) Y' = 50,5 + 22,5x1 – 15,5x2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Проверить адекватность модели (пригодность для практического применения) | Полученное уравнение регрессии необходимо проверить на адекватность исследуемому объекту. 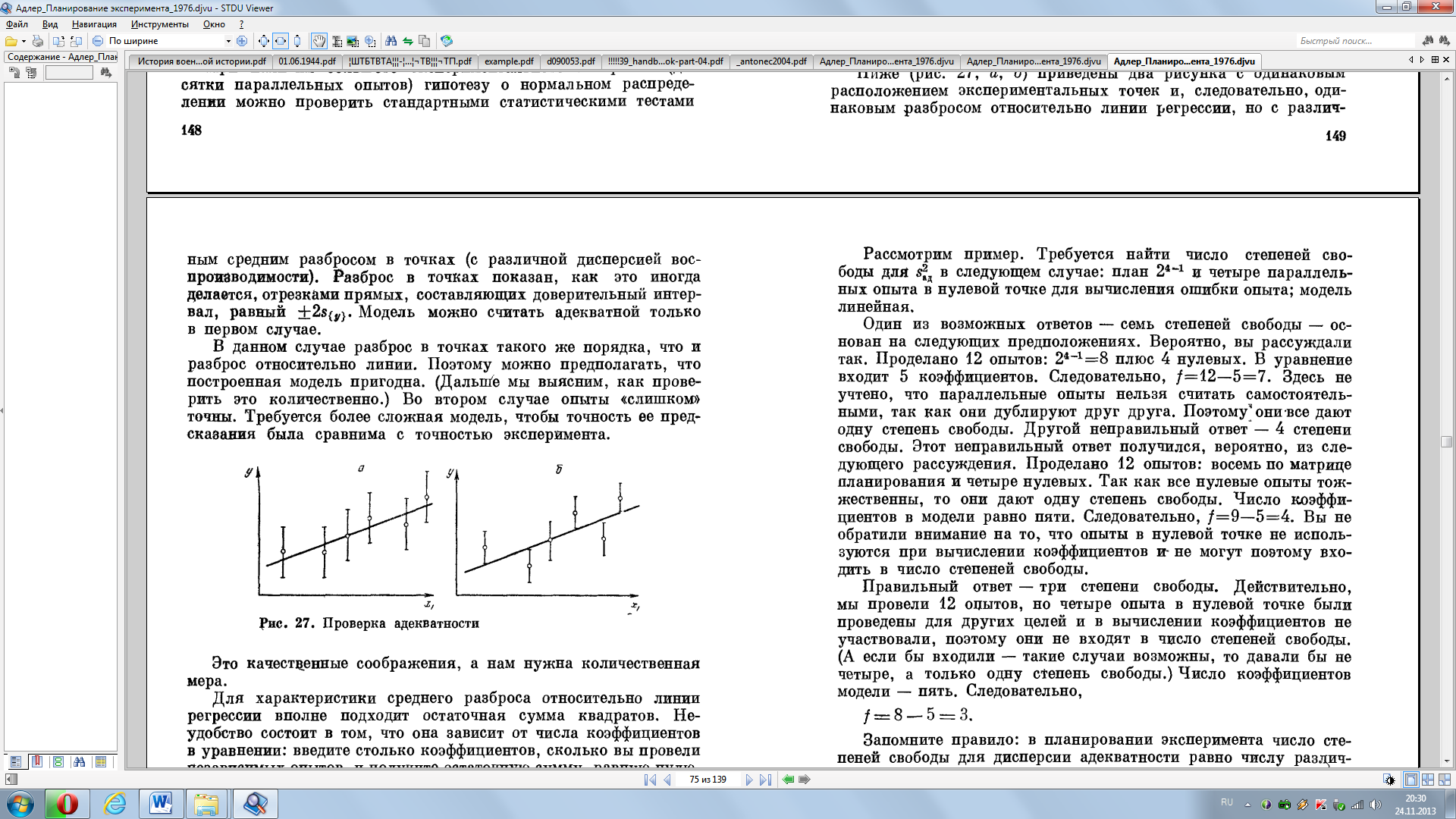 Проверка адекватности выполняется по критерию Фишера Для этой цели необходимо оценить, насколько отличаются средние значения yi выходной величины, полученной в точках факторного пространства, и значения yi, полученного из уравнения регрессии в тех же точках факторного пространства. Адекватность модели проверяют по критерию Фишера F- критерию Fp= S2ад/S2в Проверка адекватности выполняется по критерию Фишера Для этой цели необходимо оценить, насколько отличаются средние значения yi выходной величины, полученной в точках факторного пространства, и значения yi, полученного из уравнения регрессии в тех же точках факторного пространства. Адекватность модели проверяют по критерию Фишера F- критерию Fp= S2ад/S2в | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить значения функции отклика по уравнению регрессии | Для рассматриваемого примера получаем: Y'1 =50,5 +22,5 (–1) – 15,5 (–1 ) = 43,5; Y'2 =50,5 +22,5 (+1) – 15,5 (–1 ) = 88,5; Y'3 =50,5 +22,5 (–1) – 15,5 (+1 ) = 12,5; Y'4 =50,5 +22,5 (+1) – 15,5 (+1 ) = 57,5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить оценку дисперсию адекватности | 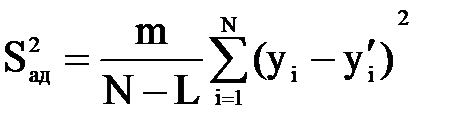 , где L – число значимых коэффициентов. , где L – число значимых коэффициентов. | Рассчитаем оценку дисперсии адекватности: S2ад = 3[(42 – 43,5)2 + (90 – 88,5)2 + (14 – 12,5)2 + (56 – 57,5)2]/(4 – 3) = 27 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить оценку генеральную дисперсию воспроизводимости | Оценкой дисперсии воспроизводимости S2в, характеризующая точность одного измерения, является средняя из всех построчных дисперсий 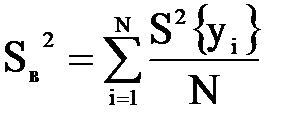 | S2в = (43 + 16 + 12 + 4)/4 = 18,75 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Задать уровень значимости | a = 0,05 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вычислить критерий Фишера | Fp= S2ад/S2в | Fp = S2ад/S2в = 27/18,75 = 1,44. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Определить число степеней свободы | fад = N – l fв = N(m - 1) | fад = (4 – 3) = 1 и fв= 4 (3 – 1)=8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Найти табличные значения F- критерию | Найденное расчетным путем Fp сравнивают с табличным значением Fт ,которое определяется при уровне значимости a и числе степеней свободы fад = N – l - по горизонтали (f2) fв = N(m - 1) – по вертикали (f1) 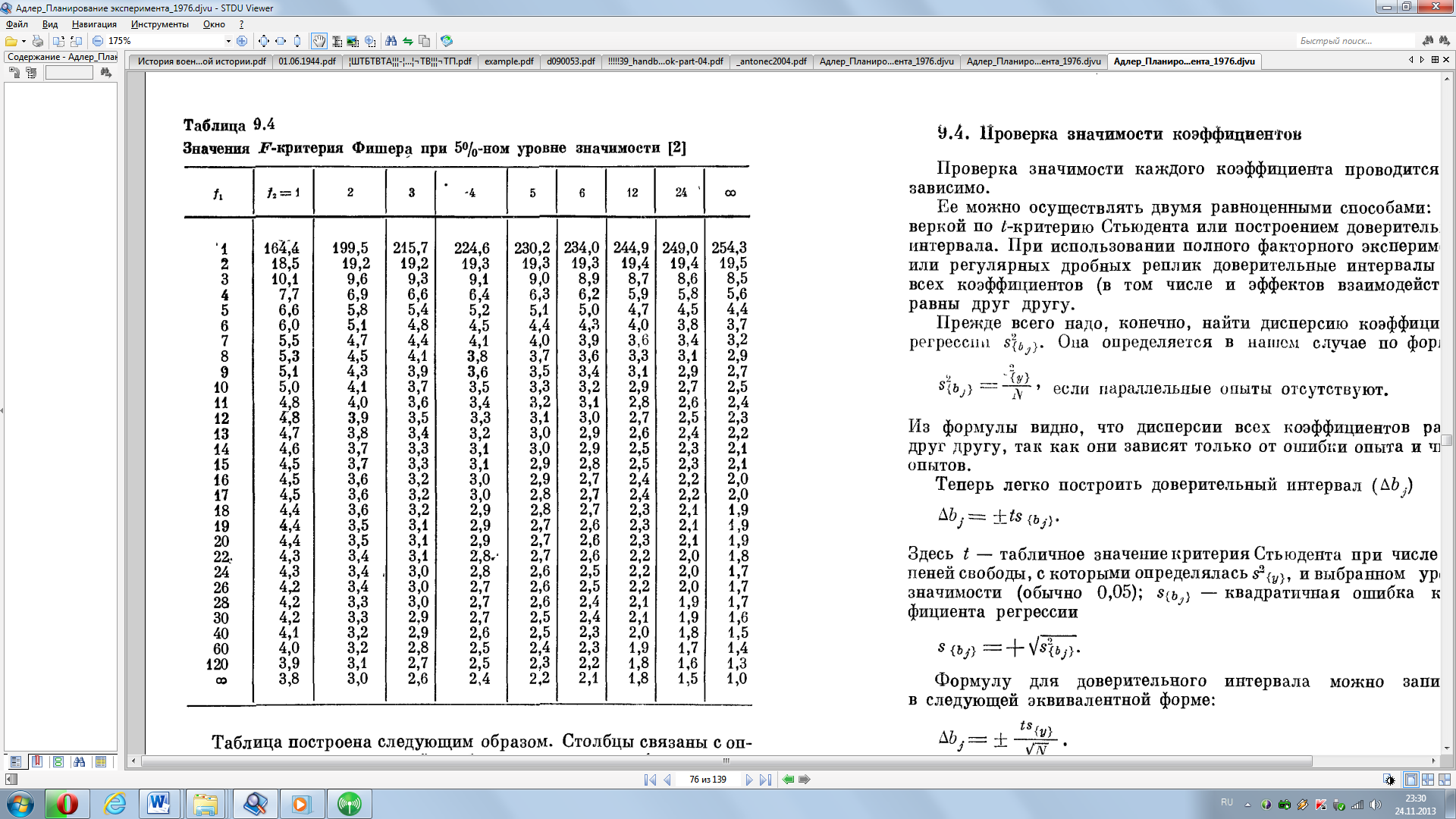 | Табличное значение коэффициента Фишера при уровне статистической значимости a =0,05 и числе степеней свободы fад = (4 – 3) = 1 и fв= 4 (3 – 1)=8 будет Fт=5,32 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сравнить расчетное значение критерия с табличным и сделать вывод об адекватности модели | Если Fp < Fт, то полученная математическая модель с принятым уровнем статистической значимости a адекватна экспериментальным данным | Следовательно, при выбранном уровне статистической значимости полученная в результате эксперимента регрессионная модель вида y' = 50,5 + 22,5x1 – 15,5x2 адекватна исследуемому объекту | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17. Преобразовать уравнение регрессии в нормированных значениях факторов в уравнение с натуральными значениями факторов | Подставить в уравнение регрессии значения факторов в натуральных значениях по формуле Y = b0 + b1 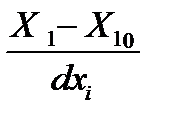 + b2 + b2 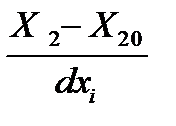 +b12 +b12 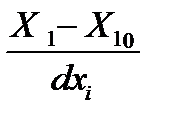 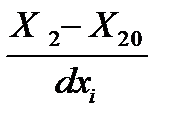 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18. Оформить отчет по результатам работы | СОДЕРЖАНИЕ И ОФОРМЛЕНИЕ ОТЧЕТА 1. Титульный лист, содержащий информацию о студенте (группа, фамилия, номер варианта); 2. Результаты подготовки (выбранные по варианту значения экспериментальных данных); 3. Основные теоретические положения (используемые формулы); 4. Результаты подготовки (матрица планирования в виде таблицы); 5. Листинг программы (язык программирования не имеет значения); 6. Ответы на контрольные вопросы; 7. Результат выполнения работы; 8. Выводы по лабораторной работе. |
Основная учебная литература
1. Сидняев Н.И. Теория планирования эксперимента и анализ статистических данных: учебн. пособ. / Н.И. Сидняев. – М.: Изд-во Юрайт, 2011.- 399с.
2.Гмурман В.Е. Теория вероятностей и математическая статистика: учеб.пособ.-12-е изд., перераб. / В.Е. Гмурман.- М.: Изд-во Юрайт, 2010.- 479с.
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебн. пособ. -12-е изд., перераб. / В.Е. Гмурман. – М.: Высшобраз.,2006. – 476с.
4 Боровков, А.А. Математическая статистика: Учебник / А. А. Боровков. – Изд. 4-е, стер. – Санкт-Петербург; М.; Краснодар: Лань, 2010. – 703 с.. (электронный ресурс).
Дополнительная учебная и справочная литература.
5 Короткова, Е. И. Планирование и организация эксперимента: учебное пособие [для хим. специальностей вузов] / Е. И. Короткова; Федер. агентство по образованию, Гос. образоват. учреждение высш. проф. образования, «Нац. исслед. Томск. политехн. ун-т». – Томск: Изд-во Том. политехн. ун-та, 2010. – 123 с.: a-ил.
6 Организация и планирование эксперимента: метод. указания к курсовой работе студентов специальности 150102 «Металлургия цв. металлов» оч. формы обучения / Иркут. гос. техн. ун-т; сост. О. В. Белоусова, Е. Г. Садохина . – Иркутск: Изд-во ИрГТУ, 2009. – 28 с.:
7 Организация и планирование эксперимента: программа, метод. указания и контр. работы для специальности 150102 «Металлургия цв. металлов» оч. формы обучения / Иркут. гос. техн. ун-т; сост. О. В. Белоусова, В. И. Щепин . – Иркутск: Изд-во ИрГТУ, 2009. – 35 с.: a-ил.
8 Альбом наглядных пособий по общей теории статистики: учеб. пособие для высш. с.-х. учеб. заведений по экон. спец. / С.С. Сергеев. – М.: Финансы и статистика, 1991. – 79 с.: a-ил.
9 Айвазян, С. А. Прикладная статистика в задачах и упражнениях :Учеб. для экон. специальностей вузов / С. А. Айвазян, В. С. Мхитарян . – М.: ЮНИТИ-Дана, 2001. – 270 с. : a-ил.
10 Афанасьева, Н. Ю. Вычислительные и экспериментальные методы научного эксперимента: Учеб. Пособие. / Н. Ю. Афанасьева. – М.: КНОРУС, 2010. – 330 с.: a-ил.
11 Барра, Ж.-Р. Основные понятия математической статистики/ Ж.-Р. Барра; пер. с фр. Ж-Р Барра. – М.: Мир, 1974. – 275 с.
12 Математическая статистика в разведочном бурении: справ.пособие / Рубен Александрович Ганджумян. – М.: Недра, 1990. – 224 с. : a-ил.
13 Горелова, Г. В. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel : учеб.пособие / Г. В. Горелова, И. А. Кацко. – [2-е изд., испр. и доп.]. – Ростов н/Д: Феникс, 2002. – 395 с.
14 Вычисления в MathCAD / Д. А. Гурский. – Минск: Новое знание, 2003. – 813 с.: a-ил.
15 Ликеш И. Основные таблицы математической статистики / Иржи Ликеш; Перевод с чеш. Ю. А. Данилова. – М.: Финансы и статистика, 1985. – 356 с.: a-ил.
16 Математическая статистика на персональном компьютере (на основе программы MicrosoftExcel) : практикум для студентов фак. технологии и компьютеризации машиностроения / сост. Г. Д. Гефан; Иркут.гос. техн. ун-т. – Иркутск: ИрГТУ, 2000. – 20 с.: a-ил. – (Высшая математика).
17 Сидняев, Н. И. Теория планирования эксперимента и анализ статистических данных: учебное пособие для магистров по специальности «Прикладная математика» / Н. И. Сидняев. – Москва: Юрайт, 2011. – 399 с.: a-ил.
1. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. М.: Наука, 1976.
2. Асатурян В.И. Теория планирования эксперимента: Учеб. пособие для втузов. М.: Радио и связь, 1983.
3. Налимов В.В. Теория эксперимента. М.: Наука, 1971.
4. Планирование и организация измерительного эксперимента / Е.Т. Володаpский, Б.Н. Малиновский, Ю.М. Туз.-К.: В.ш. Головное изд-во, 1987.
ВАРИАНТ 1
Sгл - глинистость,
К кар ~ карбонатность.
|
|
ВАРИАНТ 2
Кпес. - песчанистость,
Ккар ~ карбонатность.
|
|
ВАРИАНТ 3
Кпор - пористость,
Кпр - проницаемость,
|
|
ВАРИАНТ 4
Sгл - глинистость,
Кпр - проницаемость,
|
|
Вариант 5.
|
|
Вариант 6
|
|
ВАРИАНТ 7
|
|
ВАРИАНТ 8
|
|
ВАРИАНТ 9
|
|
ВАРИАНТ 10