Примеры на вычисление производной
а) 2 в) Найти производную функции 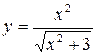 .
.
При нахождении производной используем формулы 6 (производная частного) и 7 (производная степенной функции).
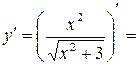
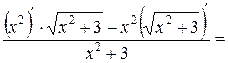
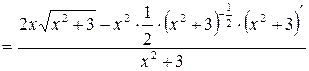 ;
;
т.к. 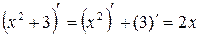 , то
, то
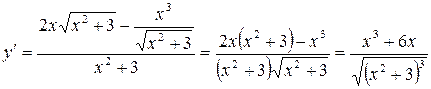 .
.
Функцию 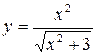 можно записать в виде произведения двух функций
можно записать в виде произведения двух функций 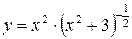 , и для вычисления производной использовать формулу 5.
, и для вычисления производной использовать формулу 5.
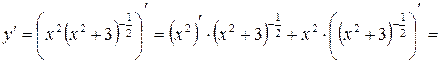
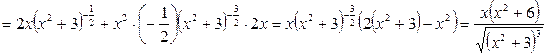 .
.
г) 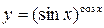 .
.
Для вычисления производной степенно-показательной функции можно использовать следующую формулу: 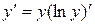 .
.
Эту формулу рекомендуется использовать в тех случаях, когда с помощью свойств логарифмов функцию 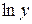 удается преобразовать и сделать более простой для дифференцирования.
удается преобразовать и сделать более простой для дифференцирования.
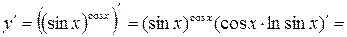
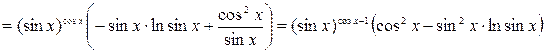 .
.
д) Производная функции 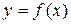 , заданной параметрически
, заданной параметрически 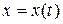 ,
, 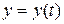 , вычисляется по формуле
, вычисляется по формуле
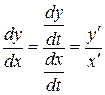 ,
,
где 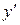 и
и 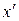 – это производные функций по переменной
– это производные функций по переменной 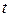 .
.
Найдем производную функции, заданной параметрически: 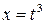 ,
, 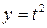 .
.
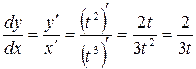 .
.
131 – 140.Производная от производной функции 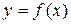 называется производной второго порядка этой функции и обозначается
называется производной второго порядка этой функции и обозначается 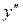 или
или 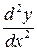 .
.
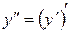 .
.
Вычислим производную второго порядка функции 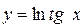 .
.
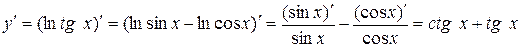 .
.
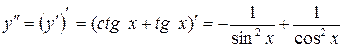 .
.
141 – 150. Если при 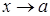 выражение
выражение 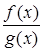 является неопределенностью типа
является неопределенностью типа 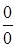 или
или 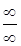 и
и
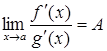 , то
, то 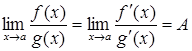 .
.
Этот способ вычисления называется правилом Лопиталя.
Неопределенности других типов с помощью алгебраических преобразований могут быть сведены к неопределенности 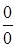 или
или 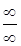 .
.
При вычислении пределов наряду с правилом Лопиталя следует использовать другие способы вычисления, а также свойства пределов.
Вычислим 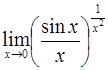 .
.
Так как 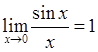 ,
, 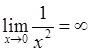 , то имеем неопределенность типа
, то имеем неопределенность типа 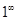 .
.
Для раскрытия такой неопределенности воспользуемся следующим утверждением.
Если при 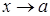 функция
функция 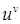 является неопределенностью типа
является неопределенностью типа 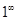 и существует
и существует
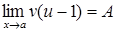 ,
,
то
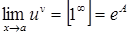 .
.
В нашем случае 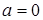 ,
, 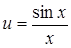 ,
, 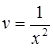 .
.
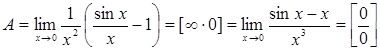 ;
;
применим правило Лопиталя:
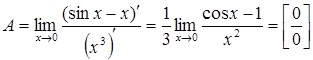 ;
;
еще раз используем правило Лопиталя:
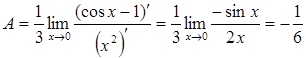 .
.
Таким образом,
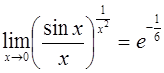 .
.
151 – 160. Полное исследование функции 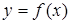 можно свести к 3 этапам.
можно свести к 3 этапам.
1 этап. Найти область определения функции; исследовать функцию на чётность, нечётность, периодичность; найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции. Установить характер точек разрыва (если они существуют), а так же найти асимптоты графика функции: вертикальные и наклонные.
Наклонные асимптота кривой 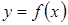 , если они существуют, задаются уравнениями вида y = kx+b , где параметры k и b определяются формулами:
, если они существуют, задаются уравнениями вида y = kx+b , где параметры k и b определяются формулами:
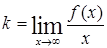 ,
, 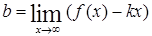 .
.
При этом пределы могут быть различными при x®+¥ или x®2¥ .
Для существования вертикальной асимптоты в точке x=x0 необходимо, чтобы хотя бы один из пределов 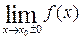
 был бесконечен.
был бесконечен.
2 этап. Исследование функции с помощью производной. Найти производную y'(x) и её критические точки (т.е. точки из области определения функции, в которых производная равна нулю или не существует), определить промежутки возрастания и убывания функции и точки экстремума.
3 этап. Исследование функции с помощью производной второго порядка. Найти производную второго порядка 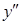 (x) и её критические точки, используя знак производной, определить промежутки выпуклости, вогнутости графика и точки перегиба.
(x) и её критические точки, используя знак производной, определить промежутки выпуклости, вогнутости графика и точки перегиба.
Используя результаты исследования нужно построить график функции.
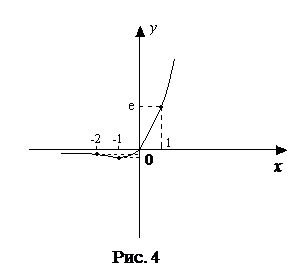
Пример. Исследовать функцию y = x× ex и построить её график.
1 этап. D(y) = (2¥ ; +¥).
Точки пересечения графика с осями координат: х = 0, y = 0 (график проходит через начало координат). Функция не является чётной ( y(2x)¹ y(x)), нечётной (y(2x)¹2y(x)), периодической.
Интервалы знакопостоянства функции:
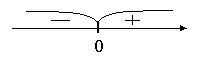
Границами интервалов, где функция сохраняет знак, могут быть только точки пересечения графика функции с осью Ох, точки разрыва и границы области определения функции.
Для исследуемой функции такой точкой является x = 0. При х<0 функция принимает отрицательные значения, при x>0 функция принимает положитель- ные значения.
Вертикальных асимптот график функции не имеет, так как она непрерывна на всей числовой прямой.
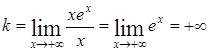 , наклонной асимптоты нет, но есть горизонтальная асимптота у=0, т.к.
, наклонной асимптоты нет, но есть горизонтальная асимптота у=0, т.к. 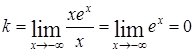 ;
; 
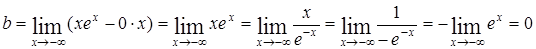
(использовалось правило Лопиталя).
2 этап.
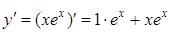 ,
, 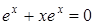 ,
, 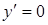 при
при 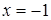 . Это критическая точка.
. Это критическая точка.
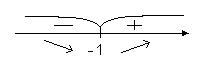
При 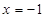 функция достигает минимума,
функция достигает минимума, 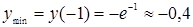 .
.
3 этап.
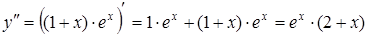 ;
;
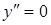 при
при 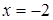 .
.
|
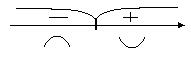
Точка x = -2 является точкой перегиба, так как производная второго порядка меняет знак в этой точке; при xÎ(-¥; -2) график является выпуклым, а на интервале (-2; +¥) – вогнутым.
y(-2) = -2 e –2 »-0.3 .
Построение графика лучше начинать с проведения асимптот (если они есть), потом отмечаются точки экстремума, точки перегиба, точки пересечения с осями. Если этих точек недостаточно, то можно найти ещё несколько дополнительных точек.
График данной функции изображен на рис. 4.
 |
1612170.В этих задачах величину, принимающую наибольшее или наименьшее значение, нужно записать как функцию некоторой переменной, а затем найти наибольшее или наименьшее значение этой функции.
Пример. Тело представляет собой цилиндр, завершенный сверху полушаром. Какую наименьшую площадь полной поверхности может иметь тело, если его объем равен 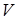 ?
?
Решение.
Пусть 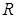 – радиус основания цилиндра,
– радиус основания цилиндра, 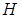 – высота цилиндра. Тогда площадь полной поверхности тела
– высота цилиндра. Тогда площадь полной поверхности тела 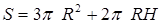 , а объем тела
, а объем тела 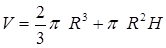 ; отсюда
; отсюда 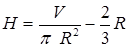 .
.
Значит, 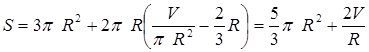 . Таким образом, найдена площадь полной поверхности тела как функция радиуса
. Таким образом, найдена площадь полной поверхности тела как функция радиуса 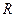 . При этом можно заметить, что
. При этом можно заметить, что 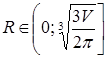 . Осталось найти наименьшее значение функции
. Осталось найти наименьшее значение функции 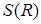 .
.
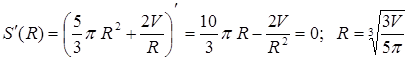 .
.
 | |||
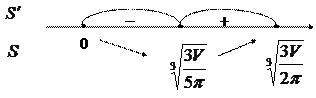 |
Следовательно, функция 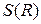 при
при 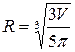 имеет наименьшее значение.
имеет наименьшее значение.
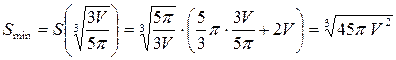 .
.
Таким образом, наименьшая площадь поверхности тела равна 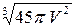 .
.
Контрольная работа №4
171 – 180.Если закон движения точки на прямой задан функцией 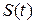 , то
, то 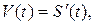
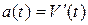 . Для нахождения
. Для нахождения 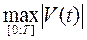 нужно найти критические точки функции
нужно найти критические точки функции 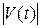 , вычислить значение
, вычислить значение 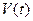 в критических точках, принадлежащих отрезку
в критических точках, принадлежащих отрезку 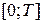 , и на концах этого отрезка и выбрать из полученных значений наибольшее по модулю. Точно так же находим
, и на концах этого отрезка и выбрать из полученных значений наибольшее по модулю. Точно так же находим 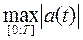 .
.
181 – 190.Функция 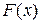 называется первообразной для функции
называется первообразной для функции 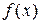 , если
, если 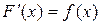 . Совокупность всех первообразных для функции
. Совокупность всех первообразных для функции 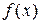 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 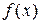 и обозначается
и обозначается 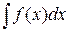 , при этом
, при этом 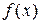 называется подынтегральной функцией,
называется подынтегральной функцией, 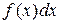 – подынтегральным выражением.
– подынтегральным выражением.
Можно доказать, что 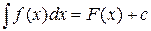 , где
, где 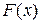 – некоторая первообразная для
– некоторая первообразная для 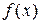 ,
, 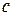 – произвольная постоянная.
– произвольная постоянная.
Для вычисления неопределенных интегралов нужно знать основные свойства, табличные интегралы и методы интегрирования.
Основные свойства неопределенных интегралов:
1. 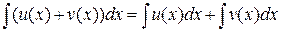 .
.
2. 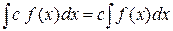 , где
, где 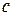 – постоянная, не равная нулю.
– постоянная, не равная нулю.
3. 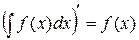 .
.
4. 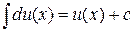 .
.
Свойства 3 и 4 показывают, что операции дифференцирования и интегрирования являются взаимообратными.
Таблица неопределенных интегралов
1) 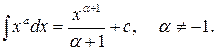
2) 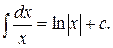
3) 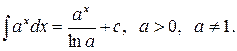
Если 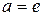 , то
, то 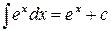 .
.
4) 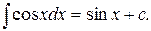
5) 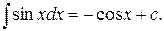
6) 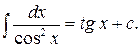
7) 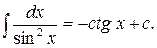
8) 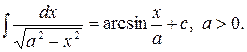
9) 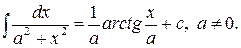
10) 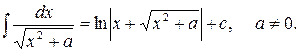
11) 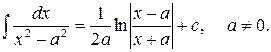
Все формулы справедливы также в случае, если переменную 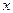 заменить на некоторую другую функцию. Так, если в формуле 2 заменить
заменить на некоторую другую функцию. Так, если в формуле 2 заменить 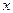 на
на 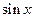 , то получим,
, то получим,
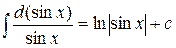 .
.
Перейдем к рассмотрению методов интегрирования.
