Дробно-линейная функция

Линейная функция является частным случаем функции вида:

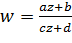(2.2.1)

где 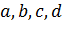– комплексные число, при чем .

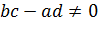Функции вида (2.2.1) называются дробно-рациональными.

Дробно-линейную функцию можно распространять на всю расширенную комплексную плоскость.

Так как 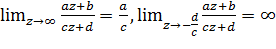, то точка 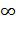переходит при этом отображении в 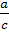, а точка 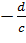в .

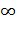Рассмотрим основные свойство дробно-линейных отображений.

1. Конформность.

Дробно линейная функция конформно отображает расширенную комплексную плоскость на расширенную комплексную плоскость.

Очевидно, что функция (2.2.1) регулярна во всей расширенной комплексной плоскость, за исключением точки 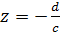– полюса первого порядка. Решая уравнение (2.2.1) относительно , находим функцию

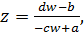(2.2.2)

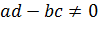( ) обратную к функции (2.2.1).

Функция (2.2.2) однозначна на всей расширенной комплексной плоскости и так же дробно-линейной. Следовательно, дробно-линейная функция однолистна в расширенной комплексной плоскости.

2. Групповое свойство.

Совокупность дробно-линейных отображений образует группу, т.е.

1)суперпозиция дробно-линейных отображений является дробно-линейным отображением.

2) Отображение, обратное к дробно-линейному, так же является дробно-линейным.

Докажем первое свойство. Пусть

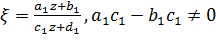(2.2.3)

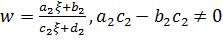(2.2.4)

Подставляя (2.2.3) в (2.2.4) получаем:

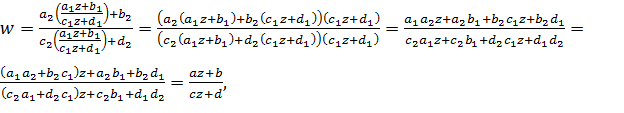где

.

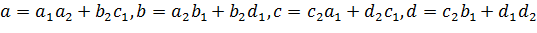Второе свойство доказано в предыдущем пункте.

2. Круговое свойство.

При дробно-линейном отображении образом любой окружности или прямой является окружность или прямая.

Докажем это свойство. Сначала рассмотрим линейное отображение 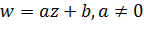. Это отображение сводится к подобию, повороту и переносу (пункт 1). Следовательно, линейное отображение переводит окружности в окружности, а прямые – в прямые.

В случае, когда дробно-линейная функция 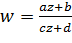не является линейной 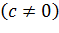, представим её в виде

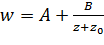, (2.2.5)

где 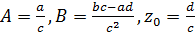. Тогда отображение (2.2.5) сводится к последовательному выполнению следующих отображений:

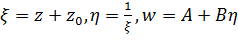(2.2.6)

Первое и третье отображения (2.2.6) обладают круговым свойством, так как они линейные. Остается доказать, что второе отображение (2.2.6), т.е. отображение

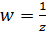, (2.2.7)

так же обладает круговым свойством.

Уравнение любой окружности или прямой на плоскости 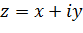имеет вид

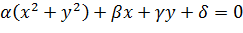(2.2.8)

(если 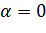, то (3.2.9) – уравнение прямой).

Так как 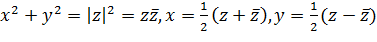, то уравнение (2.2.8) записывается в виде

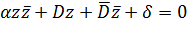, (2.2.9)

где .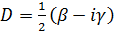

Подставив в (2.2.9) 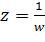получаем

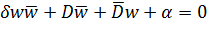. (2.2.10)

Следовательно, образом окружности (2.2.9) (прямой, если 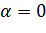) при отображении (2.2.7) является окружность (2.2.10) (прямая, если ).

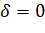Отметим, что дробно-линейное отображение 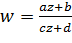переводит окружности и прямые, проходящие через точку 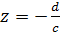в прямые, а остальные окружности и прямые – в окружности.

Принято считать, что прямая – это окружность бесконечного радиуса. Поэтому коротко круговое свойство можно сформулировать так: при дробно-линейном отображении окружности переходят в окружности.

4. Свойство сохранения симметрии.

Понятие симметрии относительно окружности определяется в элементарной геометрии следующим образом. Пусть 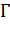– окружность радиуса 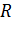с центром в точке .

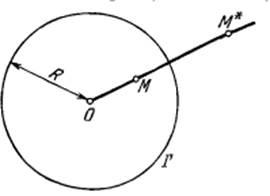Определение. Точки и называются симметричными относительно окружности , если они лежат на одном луче, выходящем из точки , и 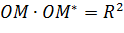(Рис. 3.2.1).

Рисунок 2.2.1.

В частности, каждая точка окружности является симметричной сама себе относительно этой окружности.

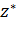Таким образом, на комплексной плоскости точки и являются симметричными относительно окружности 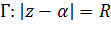, если они лежат на одном луче, выходящем из точк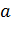и и 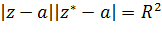. Из этого определения вытекает, что симметричными относительно окружност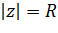и точки , 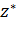связаны соотношением

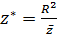(2.2.11)

В частности, симметричные относительно единичной окружности 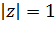точки и 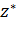связаны соотношением:

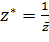(2.2.12)

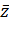Так как точки и симметрично относительно действительной оси, то из (2.2.12) следует, что точка получается из точки двойной симметрией: относительно действительной оси и относительно единичной окружность (в любом порядке).

Из (2.2.11) вытекает, что симметричные относительно окружности 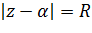точки и 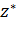связаны соотношением

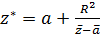(2.2.13).

Стоит отметить, что точки и 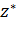являются симметричными относительно окружности 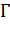тогда и только тогда, когда любая окружность 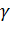, проходящая через эти точки, пересекается с окружностью 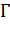под прямым углом.

Дробно-линейное отображение обладает следующим свойством сохранения симметрии.

При дробно-линейном отображении пара точек, симметричных относительно окружности, переходит в пару точек, симметричных относительно образа этой окружности.

Здесь окружность, в частности, может быть прямой.

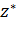Докажем это свойство. Пусть точки и симметричны относительно окружности 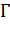и пусть дробно-линейное отображение 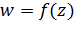переводит окружность 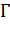в 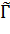, а точки и 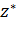– в точки и 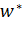соответственно. В силу кругового свойства 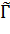является окружностью. Нужно доказать, что точки и 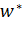симметричны относительно 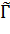. Для этого достаточно доказать, что любая окружность 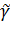, проходящая через точки и 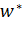, пересекается с 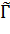под прямым углом.

Прообразом окружности 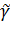при дробно-линейном отображении 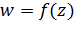является окружность 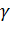, проходящая через точки и 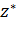. Эта окружность 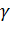пересекается с 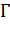под прямым углом. Следовательно, 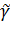пересекается с 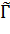так же под прямым углом, так как дробно-линейное отображение является конформным во всей расширенной плоскости и сохраняет углы между кривыми в каждой точке.

5. Дробно-линейное отображение, переводящее три точки в три точки.

Существует единственное дробно-линейное отображение, при котором три различные точки 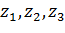переходят в три различные точки 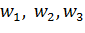. Это отображение определяется формулой

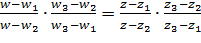(2.2.14)

Докажем это свойство. Из группового свойства следует, что функция 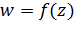, определяемая соотношением (2.2.14), является дробно-линейной. Так же ясно, что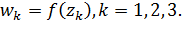

Докажем, что если дробно-линейная функция 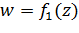удовлетворяет тем же условиям, что и 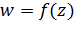,а именн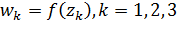о , то 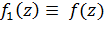. Пусть 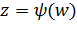– функция, обратная функции 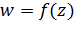. Тогда 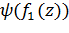– дробно-линейная функция:

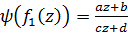и 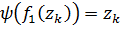. То есть ,

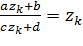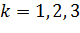
Отсюда получаем 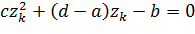,то есть квадратное уравнение 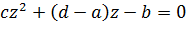имеет три различных корня. Следовательно, 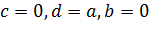и 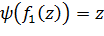, откуда 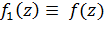.Свойство доказано.

Заметим, что функция 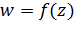,определенная формулой (3.2.15), конформно отображает круг, граница которого проходит через точки 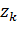, , 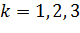на круг, граница которого проходит через точки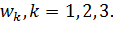

Функция Жуковского

Функция

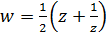(2.3.1)

называется функцией Жуковского.

Эта функция была введена в рассмотрение русским ученым Н.Е. Жуковским в теории крыла самолета и имела важные приложения, поэтому носит его имя.Эта функция регулярна в точках 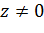, ∞, причем 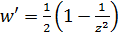в точках 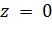и 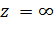имеет полюсы первого порядка. Следовательно, функция Жуковского (1) однолистна в каждой точке 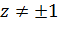, так как 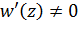при 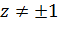, и неоднолистна в точках 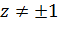,, так как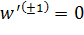

Рассмотрим основные свойства функции Жуковского.

1. Однолистность.

Функция Жуковского 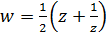однолистна в области 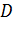тогда и только тогда, когда в этой области нет различных точек 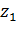и 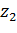, связанных равенством

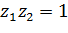(2.3.2)

В самом деле, пусть 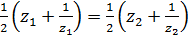. Тогда 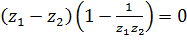, откуда либо 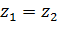, либо .

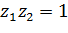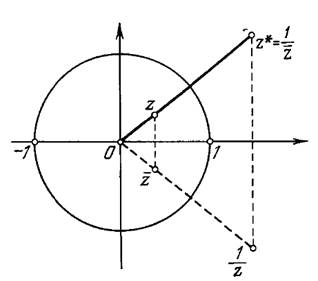Равенство (2.3.2) геометрически означает, что точка 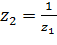, получается из точки 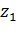двойной симметрией: относительно окружности 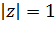и относительно прямой 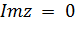(Рис. 2.3.1).

Рисунок 2.3.1.

Таким образом, функция Жуковского однолистна в области в том и только в том случае, когда эта область не содержит ни одной пары различных точек, которые получаются одна из другой двойной симметрией: относительно единичной окружности и относительно действительной оси.

Функция Жуковского 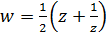однолистна в следующих областях:

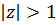· — внешность единичного круга,

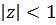· — внутренность единичного круга,

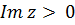· — верхняя полуплоскость

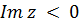· — нижняя полуплоскость

2. Образы окружностей и лучей.

Найдем образы окружностей 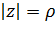и лучей 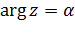(полярная координатная сетка) при отображении функцией Жуковского. Полагая в (3.3.1) 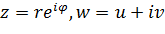, получаемы 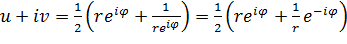, откуда применив формулы Эйлера получим:

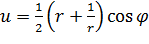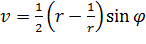, (2.3.3)

Рассмотрим окружность

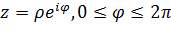(2.3.4)

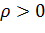( — фиксировано). Из (3.3.3) следует, что при отображении функцией Жуковского образом окружности (3.3.4) является эллипс

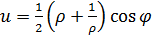, (2.3.5)

с полуосями 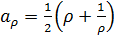, 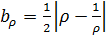и с фокусами в точках 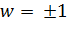(так как 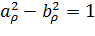). Исключаяиз уравнений (3.3.5) параметр 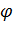, при 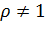уравнение этого эллипса можно записать в каноническом виде:

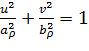(2.3.6)

Отметим, что при замене 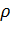на 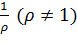эллипс (2.3.5) остается тем же самым, но его ориентация меняется на противоположную. На рис. 2.3.2 показаны окружности 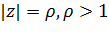, ориентированные по часовой стрелке, и их образы — эллипсы (2.3.6)

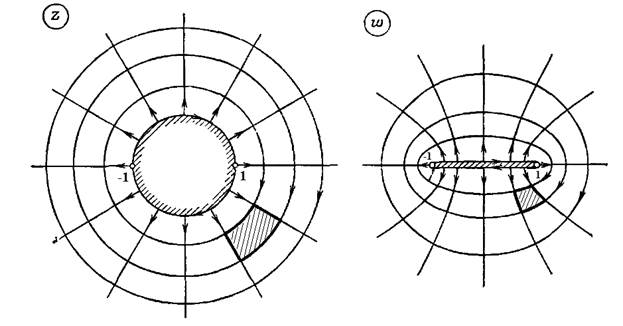
Рисунок 2.3.2.

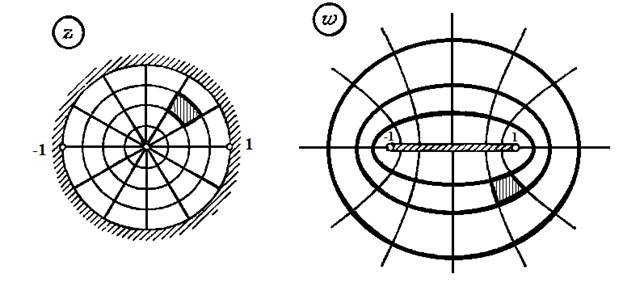
Из (2.3.5) видно, что эти эллипсы ориентированы также по часовой стрелке. На рис. 2.3.3 показаны окружности при 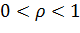и их образы — эллипсы (2.3.6); при этом ориентация меняется на противоположную: окружность 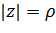, ориентированная против часовой стрелки, переходит в эллипс (2.3.6), ориентированный по часовой стрелке.

Рисунок 2.3.3.

При 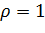эллипс (3.3.5) вырождается в отрезок 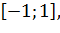проходимый дважды, т. е. окружность 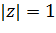переходит в отрезок [—1, 1], проходимый дважды (рис. 3.3.2, 3.3.3).

Рассмотрим луч

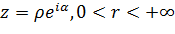(2.3.7)

( — фиксировано). При отображении функцией Жуковского образом этого луча (см. (3.3.3)) является кривая

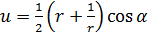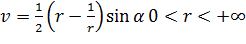, (2.3.8)

Исключаяиз уравнений (3.3.8) параметр 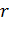, при 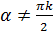( — целое), получаем

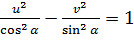(2.3.9)

Кривая (2.3.9) — гипербола с фокусами в точках 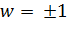и с асимптотами .

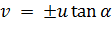Если 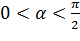, то кривая (2.3.8) является правой ветвью гиперболы (2.3.9), т. е. луч (2.3.7) при 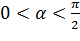переходит в правую ветвь гиперболы (2.3.9) (ориентация показана на рис. 2.3.4).

Рисунок 2.3.4.

При замене в (2.3.8) на 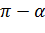получается левая ветвь той же гиперболы (2.3.9), поэтому луч (2.3.7) при 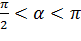переходит в левую ветвь гиперболы (2.3.9) (рис. 2.3.4). Отметим также, что при замене в (2.3.8) на 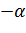получается та же ветвь гиперболы (2.3.9), но ее ориентация меняется на противоположную.

Рассмотрим лучи (2.3.7) при 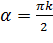( — целое). Из (2.3.8) следует, что луч 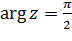переходит в мнимую ось 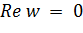(рис. 2.3.4). Луч 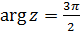также переходит в мнимую ось 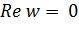. При 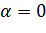кривая (2.3.8) вырождается в луч 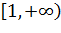проходимый дважды (сложенный вдвое) (рис. 2.3.4), т. е. луч 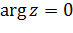переходит в луч 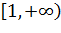, проходимый дважды: луч 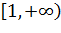переходит в луч 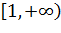и полуинтервал 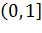– в луч 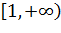(рис. 2.3.4). Аналогично, луч 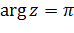переходит в луч 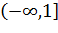, проходимый дважды (рис. 2.3.4).

Таким образом, функция Жуковского 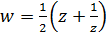переводит окружности 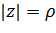в эллипсы (2.3.6), а лучи 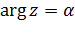– в ветви гипербол (2.3.9); фокусы всех эллипсов (2.3.6) и гипербол (2.3.9) расположены в точках 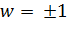; любой эллипс (2.3.6) пересекается с любой гиперболой (2.3.9) под прямым углом.

4. Функция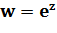

Рассмотрим основные свойства данной функции.

1. Однолистность.

Найдем условие, которому должна удовлетворять область 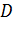, чтобы отображение

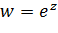(3.1.1)

было однолистным в этой области.

Если 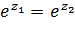, т.е. 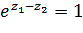, то

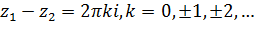(3.1.2)

Следовательно, для однолистности отображения (3.1.1) необходимо и достаточно, чтобы область 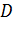не содержала никакой пары различных точек, удовлетворяющих условию (3.1.2).

2. Периодичность.

По формуле Эйлера 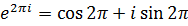=1, то для любого 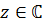имеем .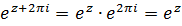

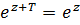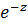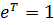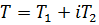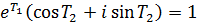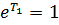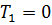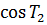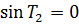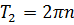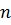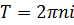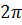С другой стороны, пусть . Умножая обе части на получаем откуда, полагая , имеем . Но тогда , то есть и =1 и , то есть , где – целое число. Таким образом, и являются основными периодами.

3. Конформность.

Так как производная функции (3.1.1) во всех точках отлична от нуля, то отображение конформно во всех точках конечной плоскости .

4. Образы точек конечной плоскости.

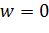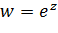Рассмотрим отображения, осуществляемые посредством этой функции. Заметим, что функция никогда не принимает значение . Это значит, что начало координат плоскости не принадлежит к образу конечной плоскости при отображении (3.1.1). Покажем, что всякая другая конечная точка плоскости принадлежит к этому образу. В самом деле, из уравнения , где 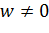задано, а 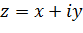– неизвестное, получаем:

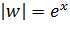, откуда 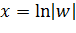и 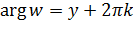, то есть .

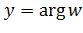Итак, прообразами точек могут быть только точки вида

.

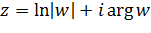Очевидно, их бесконечно много, так как 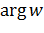имеет бесконечное множество значений, различающиеся попарно на целые кратные 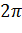. Кроме того, каждая из найденных точек действительно есть прообраз точки , так как

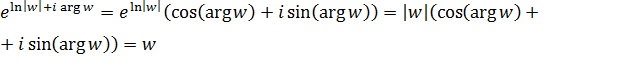. (3.1.3)

Итак, множество всех корней уравнения 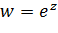, где 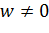представляются формулой

=

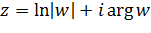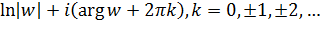
Все эти точки расположены на одной прямой, параллельной мнимой оси на расстоянии друг от друга.

То есть функция (3.1.1) отображает конечную плоскость на область, получающуюся из конечной плоскости путем исключения одной точки , при чем отображение не взаимно однозначно, так как каждая точка имеет бесконечное множество прообразов (3.1.3).

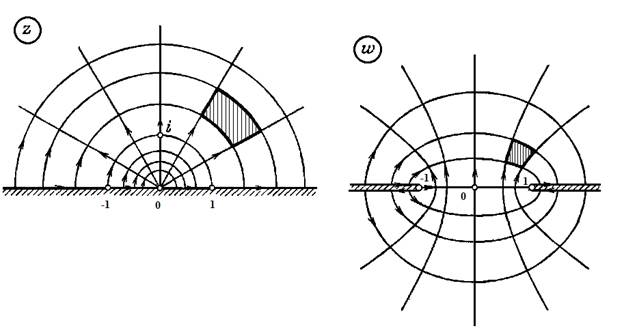
5. Образы прямых, параллельных осям координат.

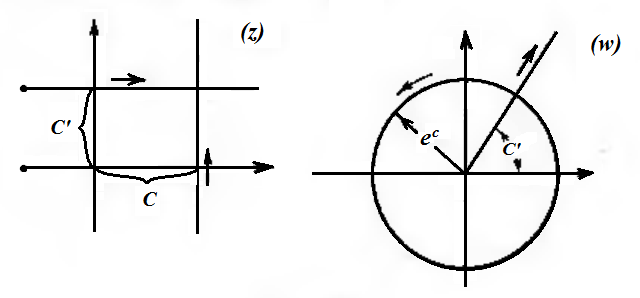
Заставим описывать какую-нибудь прямую, параллельную одной из координатных осей (Рис. 3.1.1).

Рисунок 3.1.1.

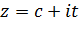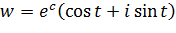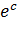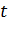Если это будет прямая , параллельная мнимой оси, то , то есть будет находиться на окружности с центром в начале координат и радиусом, равным . При этом, когда точка описывает прямую однократно так, что ордината этой точки, равная , непрерывно растет от -∞ до +∞, то описывает соответствующую окружность бесконечное множество раз в одном и том же положительном направлении.

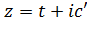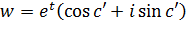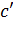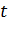Если же точка описывает прямую , параллельную действительной оси, то , очевидно, пробегает прямолинейный луч, выходящий из начала координат и образующий с положительной частью действительной оси угол . При этом, когда точка описывает однократно так, что абсцисса этой точки, равная , непрерывно растет от -∞ до +∞, то описывает соответствующий луч однократно так, что расстояние этой точки от начала координат непрерывно растет от 0до ∞ (и тот и другой пределы исключаются, так как ).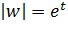

Итак, при отображении плоскости посредством функции 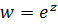семейство прямых, параллельных мнимой оси преобразуется в семейство окружностей с центром в начале координат, а семейство прямых, параллельных действительной оси, – в семейство прямолинейных лучей, выходящих из начала координат.

6. Образы полос, параллельных действительной оси.

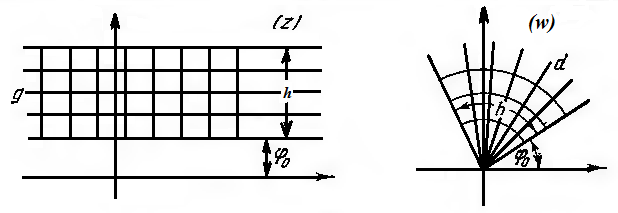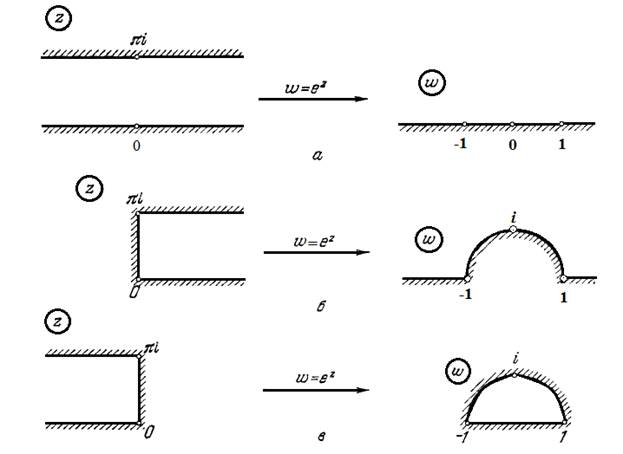
Рассмотрим область 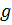, представляющую внутренность прямоугольной полосы шириной 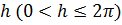, параллельной действительной оси. Пусть эта полоса ограничена линиям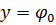и и 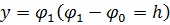. Из установленного выше следует, что образ области 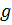в плоскости 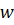будет область 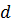, представляющая угол раствора 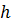с вершиной в начале координат, ограниченный прямолинейными лучам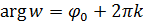и и 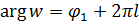(Рис. 3.1.2).

Рисунок 3.1.2.

При этом соответствие между точками областе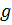й и 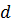, устанавливаемое посредством функции (3.4.1.), будет взаимно однозначным, поскольку прообразами некоторой точки 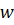из области 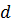могут быть только точки 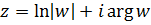, различающиеся друг от друга значениями мнимой части. Две такие точки лежат на одной прямой, параллельной мнимой оси, на расстоянии, кратном 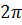. Но полоса 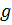имеет ширину не более 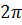, поэтому она может содержать внутри лишь один прообраз точки 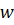. Итак, каждая точка 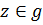имеет лишь один образ и каждая точка 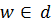лишь один прообраз внутри 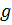, что выражает взаимную однозначность отображения.

При этом показательная функция взаимно однозначно и конформно отображает полосу ширины 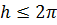, параллельную действительной оси, на угол раствора 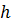с вершиной в начале координат. Поэтому к показательной функции прибегают каждый раз, когда надо отобразить некоторую прямолинейную полосу на внутренность угла.

7. Образ прямой, не параллельной ни одной из оси координат.

Если прямая плоскости не является параллельной какой-либо оси координат, то образ её в плоскости 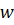будет уже не прямой и не окружностью, а логарифмической спиралью. В самом деле, если эта прямая есть 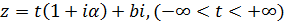( 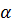– угловой коэффициент прямой, а – ордината в начале), то образом будет кривая 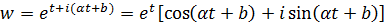. Здесь 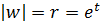, , 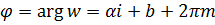или, исключая параметр 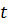: 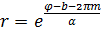. Но 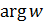или полярный угол 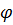определен только с точностью до целого кратного от 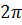. Поэтому, обозначая 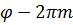снова через 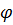получаем: 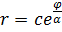, где .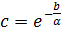

Это и есть уравнение логарифмической спирали (Рис. 3.1.3). Из того, что она является образом прямой есть 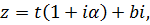пересекающей прямые, параллельные действительной оси под постоянным углом 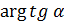, следует в силу конформности отображения, что и логарифмическая спираль пересекается под тем же углом образы указанных прямых, то есть все лучи, выходящие из начала координат. Мы получили характеристическое свойство логарифмической спирали.

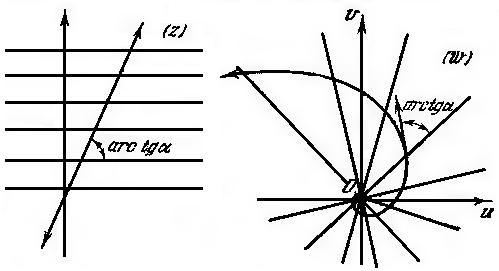
Рисунок 3.1.3.

Пример 3.1.1. Из приведенных свойств (1) и (2) вытекает, что функция 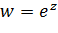конформно отображает прямоугольник 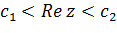, , 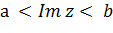где 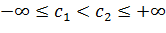, 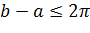на кольцевой сектор 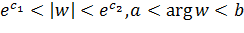. Частные случаи таких отображений показаны на рис. 3.1.4.

Рисунок 3.1.4.

Пример 3.1.2. Найдем образ отрезка 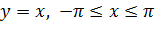при отображении .

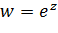Рисунок 3.1.5.

Любая точка отрезка имеет комплексную координату 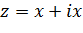, 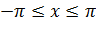. Поэтому её образом служит линия, параметрически заданная уравнениями 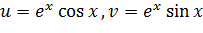. Это дуга логарифмической спирали (рис. 3.4.5).

5. Тригонометрические функци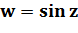и и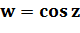

Тригонометрические функции в комплексной области просто выражаются через показательную функцию. По формуле Эйлера имеем: 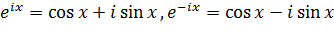, откуда , .

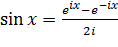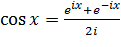Учитывая это, примем по определению для любого комплексного

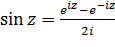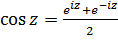, . (3.2.1)

Отметим, что функции (3.2.1) периодичны с периодом 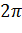.