Показатели качества регрессии

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции.

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как

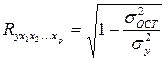, (7)

где - общая дисперсия результативного признака;

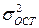- остаточная дисперсия для уравнения .

Границы изменения величины 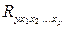- от 0 до 1. Чем ближе значение к единице, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:

.

При правильном включении факторов в регрессионный анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение факторы малозначимы, то индекс множественной корреляции может практически совпадать с индексом парной корреляции.

Для вычисления индекса множественной корреляции можно пользоваться следующей формулой

.

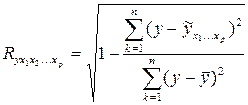Для линейного уравнения регрессии в стандартизованном масштабе формула индекса множественной корреляции может быть представлена в виде

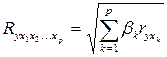. (8)

Пример. Для уравнения корреляции, полученного в предыдущем примере, вычислить индекс множественной корреляции и сравнить его с парными индексами корреляции.

Ранее были получены следующие значения:

; ; .

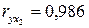Тогда по формуле (8) получаем

.

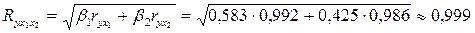Сравниваем индекс множественной корреляции с парными индексами корреляции:

.

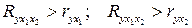Следовательно, включение обоих факторов в уравнение множественной регрессии является обоснованным.

Значимость уравнения множественной регрессии в целом оценивается с помощью с помощью F-критерия Фишера:

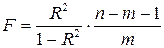, (9)

где - индекс множественной корреляции (тоже, что и );

- число наблюдений;

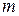- число факторов.

Полученное по формуле (9) значение F сравнивается с табличным при уровне значимости 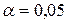. Если фактическое значение F-критерия Фишера превышает табличное, то уравнение статистически значимо с вероятностью . При использовании таблицы следует принимать .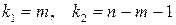

Пример. Для уравнения корреляции, полученного в предыдущих примерах, вычислить значение F-критерия Фишера и определить статистическую значимость уравнения.

Ранее был вычислен индекс множественной корреляции . По формуле (9) получаем

.

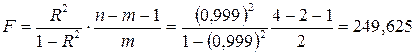По таблице определяем для значений :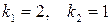

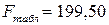
Мы видим, что , а значит полученное уравнение корреляции является статистически значимым.