Определение корня многочлена

РЕФЕРАТ

на тему:

Корни многочлена. Теорема Безу

Выполнили:

Студенты 1 курса группы ИМ-11

Очного отделения

Шабунин Дмитрий Олегович

Зорин Александр Сергеевич

Проверила:

Бобылева Оксана Владимировна

подпись___________________

Абакан

2016г.

План

Введение……………………………………………………………………………...3

1.Многочлены………………………………………………………………………..3

1.1.Определение многочлена………………………………………………………3

1.2.Определение корня многочлена……………………………………………….4

1.3.Схема Горнера………………………………………………………………….5

1.4.Нахождение корней по схеме Горнера. Виды корней……………………….7

2. Этьен Безу. Биография. Теорема Безу. Следствия из теоремы……………….13

2.1. Этьен Безу. Биогафия………………………………………………………...13

2.2. Теорема Безу………………………………………………………………….13

2.3 Следствия из теоремы Безу…………………………………………………..14

2.4. Примеры использования теоремы…………………………………………..14

Заключение………………………………………………………………………….16

Список используемых источников………………………………………………..17

ВВЕДЕНИЕ

Тема данного реферата: «Корни многочлена. Теорема Безу».

В нем мы хотим рассмотреть, что такое многочлен, что является корнем многочлена, а также рассказать про схему Горнера и теорему Безу.

В первой части мы разберем понятие многочлена, его корней и их виды и про схему Горнера. Во второй про теорему Безу.

Данная тема довольно актуальна, поскольку теорема Безу является одной из базовых теорем алгебры.

Многочлены

Понятие многочлена

Многочлен (полином) от одной переменной x – это выражение вида

,

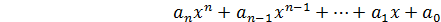где x – переменная , 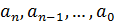– коэффициенты из некоторого числового поля, n – целое неотрицательное число, а нулевое- свободный член. Отдельные слагаемые вида ……, k=0,1, …,n называются членами многочлена.

Также многочлен называют «полиномом», этот термин происходит от греческих слов «πολι» - много и «νομχ» - член.

2 члена называются подобными, если их степени равны. При этом подобные между собой члены можно преобразовать в один, т.е. привести подобные члены.

Степенью многочлена называют наибольшую среди степеней многочлена, при этом многочлен f(x)- не тождественный нуль. Обозначается эта степень deg(f).

Например:

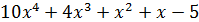-многочлен четвертой степени (старшая степень равна четырем);

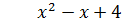- многочлен второй степени или квадратный (старшая степень равна двум).

При этом тождественный нуль степени не имеет.

Предполагается, что коэффициенты многочлена принадлежат определенному полю (полю действительных, рациональных, комплексных чисел). Так, если выполнять над многочленом операции сложения, умножения или вычитания при помощи сочетательного, переместительного и распределительных законов, мы получаем снова многочлен.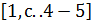

Из вышесказанного следует, что совокупность всех многочленов с коэффициентами из данного поля Р образует кольцо Р 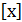- кольцо многочленов над данным полем, это кольцо не имеет делителей нуля, т.е. произведение многочленов, не равных нулю, не может дать нуль.

Определение корня многочлена

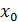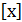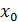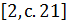Элемент кольца Р называется корнем многочлена f(x) ∈ Р , если f( )=0. Другими словами, число 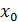является корнем многочлена f(x), если в выражение

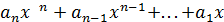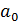+ =0

мы подставим 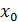, тогда получим

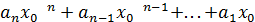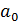+ =0.

Таким образом, при подстановке вмест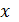о число 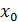получается верное выражение. Это означает, что число 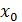является корнем равенства f(x)=0.

Поэтому корень многочлена f(x) и корень соответствующего уравнения f(x)=0 по сути одно и то же.

К примеру, найдём корень многочлена f(x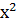)=3 -10+3

Данное выражение является квадратным поэтому для нахождения корня многочлена нам необходимо решить следующее уравнение

3 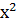-10х+3=0.

Для этого необходимо рассмотреть алгоритм решения квадратных уравнений.