Задачи, описывающие работу

Основными компонентами задач, описывающих работу, являются выполняемый объем работы, время, производительность. Эти задачи являются аналогами задач, описывающих движение: пройденный путь – аналог выполненной работы, время движения – аналог времени работы, скорость движения – аналог производительности труда. Всю работу, которую необходимо выполнить, если объем работы не указан конкретно, обычно принимают за единицу.

Задача 1. Двое рабочих выполнили всю работу за 10 дней, причем последние два дня первый из них не работал. За сколько дней первый рабочий выполнил бы всю работу, если известно, что за первые 7 дней они вместе выполнили 80 % всей работы.

Решение. Примем весь объем работы за единицу;

х – производительность труда (за день) первого рабочего;

у – производительность труда второго рабочего;

время, требуемое первому рабочему, на выполнение всей работы 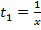(дней);

время, требуемое второму рабочему 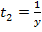(дней).

Вся работа выполнена за 10 дней, причем первый работал только 8 дней, поэтому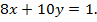

За 7 дней рабочие выполнили 80 %, или 0,8, всей работы:

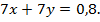
Запишем систему уравнений и решим ее:

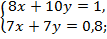
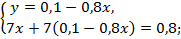
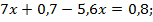
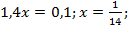
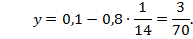
Время, требуемое первому рабочему на выполнение всей работы 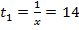дней.

Ответ: время работы первого рабочего составляет 14 дней.

Замечание. При решении данной задачи не обязательно было находить значение у, так как этого не требовалось условиями задачи.

Задача 2. На вагоноремонтном заводе в определенный срок должно быть отремонтировано 330 вагонов. Ремонтируя в среднем на 3 вагона в неделю больше, чем планировалось, на заводе уже за две недели до срока отремонтировали 297 вагонов. Сколько вагонов в неделю ремонтировали на заводе?

Решение. Пусть х – планируемая производительность (количество ремонтируемых вагонов) в неделю; (х +3) – реальная производительность; t – число запланированных недель ремонта, 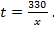За (t – 2) недели отремонтировано 297 вагонов при производительности (х + 3) вагона в неделю, поэтому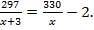

Решим полученное уравнение (по условию задачи х > 0):

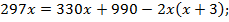
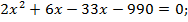
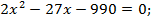
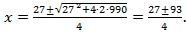
Так как 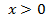, то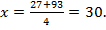

Планируемое количество отремонтированных вагонов в неделю составляло 30, реальное – на 3 вагона больше, т. е. 33 вагона в неделю.

Ответ: на заводе ремонтировали 33 вагона в неделю.

Задача 3. Трое рабочих должны сделать 80 одинаковых деталей. Известно, что все трое за один час делают 20 деталей. К работе приступил сначала первый рабочий. Он сделал 20 деталей, затратив на это более трех часов. Оставшуюся часть работы выполнили вместе второй и третий рабочие. На всю работу ушло 8 ч. Сколько часов потребовалось бы первому рабочему на всю работу, если бы с начала и до конца он делал ее один?

Решение. На первый взгляд перед нами стандартная задача на совместную работу. Но если мы будем отдельно рассматривать производительность труда каждого рабочего, а также принимать за неизвестное искомое время, то придем к системе, в которой число неизвестных превышает число уравнений. Этой неприятности можно избежать, если заметить, что второй и третий рабочий трудятся совместно, значит можно рассматривать только их совместную производительность.

Пусть производительность первого рабочего составляет х деталей в час, а совместная производительность второго и третьего рабочих равна у деталей в час. В течение t часов первый рабочий трудился один, причем из условий задачи известно, что 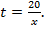А оставшиеся 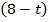часов работу выполняли второй и третий рабочие, которые изготовили 60 деталей. Тогда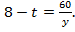

Запишем условия в систему 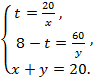и укажем дополнительное условие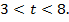

Решим систему:

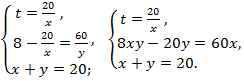
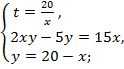
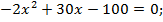
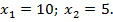
Согласно условию 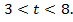поэтому 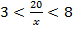. Значение х₁ = 10 не соответствует этому условию, следовательно х = 5. Искомая величина 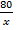составляет

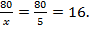
Ответ: первому рабочему потребовалось бы 16 ч.