Формула Пуассона. Простейший поток событий
Пусть в эксперименте проводятся повторные испытания по схеме Бернулли и число испытаний 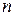 велико
велико 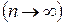 , вероятность
, вероятность 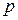 появления наблюдаемого события
появления наблюдаемого события 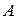 в одном испытании мала
в одном испытании мала 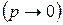 , а параметр
, а параметр 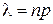 является постоянной величиной. Тогда для вероятности
является постоянной величиной. Тогда для вероятности 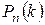 — вероятности того, что событие
— вероятности того, что событие 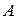 в
в 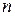 испытаниях появится
испытаниях появится 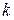 раз, справедливо соотношение
раз, справедливо соотношение
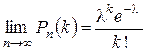 . (3.1)
. (3.1)
При вычислении вероятности 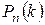 в таком случайном эксперименте можно использовать приближенную формулу
в таком случайном эксперименте можно использовать приближенную формулу
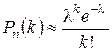 , (3.2)
, (3.2)
которая называется формулой Пуассона, а число 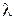 — параметром Пуассона.
— параметром Пуассона.
Задача 3.1. Вероятность брака при изготовлении некоторого изделия равна 0,008. Найти вероятность того, что при контроле среди 500 изделий будет не более двух бракованных.
Решение: поскольку вероятность 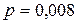 мала, а число испытаний
мала, а число испытаний 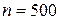 велико, то можно применить формулу Пуассона с параметром
велико, то можно применить формулу Пуассона с параметром 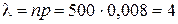 . Искомая вероятность является вероятностью суммы трех событий: бракованных изделий оказалось два, одно или ни одного. Поэтому
. Искомая вероятность является вероятностью суммы трех событий: бракованных изделий оказалось два, одно или ни одного. Поэтому
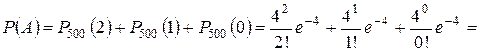
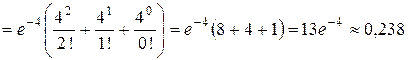 .
.
Определение 3.1
Потоком событий называется последовательность событий, наступающих в случайные моменты времени.
Например,потоком событий будут вызовы, поступающие на АТС, сигналы при сеансе радиосвязи, сообщения, поступающие на сервер, и.т.д.
Определение 3.2
Поток событий называется пуассоновским (простейшим) если он обладает следующими свойствами:
1. Свойством стационарности, т.е. интенсивность потока 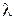 — постоянная.
— постоянная.
2. Свойством ординарности, т.е. появление двух или более событий за малый промежуток практически невозможно.
3. Свойством отсутствия последействия, т.е. вероятность появления 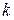 событий за промежуток времени
событий за промежуток времени 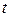 не зависит от того, сколько событий появилось на любом другом участке.
не зависит от того, сколько событий появилось на любом другом участке.
Если обозначить 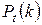 — вероятность появления
— вероятность появления 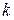 событий пуассоновского потока c интенсивностью
событий пуассоновского потока c интенсивностью 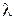 за время
за время 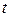 , то справедлива формула:
, то справедлива формула:
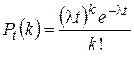 . (3.3)
. (3.3)
Задача 3.2. Страховая компания обслуживает 10000 клиентов. Вероятность того, что в течение одного дня клиент обратится в компанию, равна 0,0003. Какова вероятность того, что в течение двух дней в нее обратятся 4 клиента?
Решение: Интенсивность 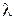 потока клиентов в течение одного дня равна
потока клиентов в течение одного дня равна
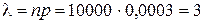 , а
, а 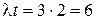 .
.
Следовательно, 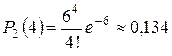 .
.
Решение задач 3.1 и 3.2 в среде Mathcadпоказано на рис. 3.

Рис. 3
Задача 3.3. Вероятность сбоя считывающего устройства турникета метрополитена в течение часа мала. Найти эту вероятность, если вероятность того, что за 8 часов будет хотя бы один сбой, равна 0,98, и если известно, что за час через турникет проходит в среднем 1000 человек?
Решение: По формулам (1.3) и (3.3) при 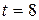 вероятность
вероятность 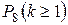 того, что в течение 8 часов будет хотя бы один сбой, равна:
того, что в течение 8 часов будет хотя бы один сбой, равна:
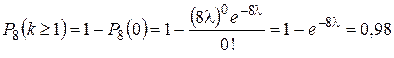 .
.
Тогда 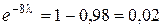 ,
, 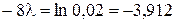 и
и 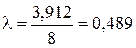 .
.
Обозначим искомую вероятность через 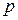 и учтем, что
и учтем, что 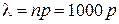 . Поэтому
. Поэтому 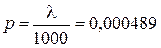 .
.
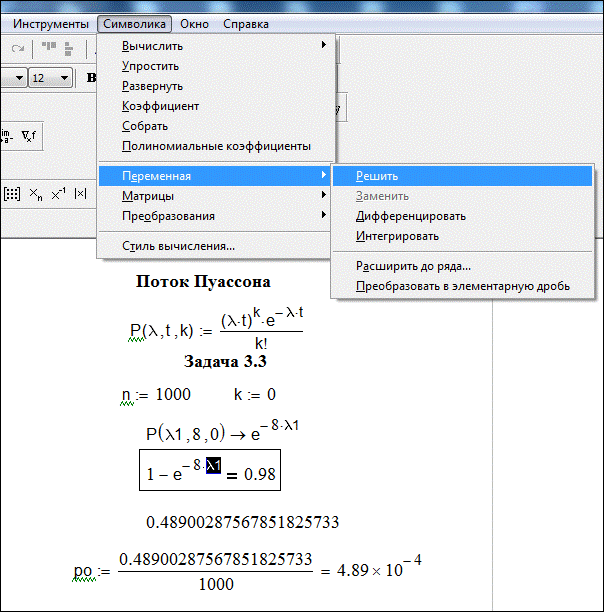
Рис. 4
Решение задачи 3.3 в среде Mathcadпоказано на рис. 4.
Здесь описана через оператор присваивания формула потока Пуассона, а затем с помощью этой функции получено значение потока при заданных 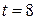 и
и 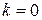 в виде функции от его интенсивности
в виде функции от его интенсивности 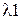 .
.
Далее используется формула Бернулли (1.3) для вероятности того, что за 8 часов будет хотя бы один сбой, которая приравнивается 0,98. Полученное уравнение решается относительно параметра Пуассона 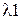 с помощью символьных команд, а затем определяется искомая вероятность
с помощью символьных команд, а затем определяется искомая вероятность 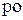 .
.
