Программная реализация метода простой итерации для решения СЛАУ в пакете MATLAB
Входные параметры: U – расширенная матрица коэффициентов, eps – требуемая точность решения.
Function res = Jakobi(U,eps);
%проверка 1
[n, m] = size(U);
if (n ~= m-1)
error ('Неверно задана система');
end;
%приведение системы к диагонально доминирующему виду
for j=1:m
for i=1:n
U1(i,j)=-U(i,j)/U(i,i);
end
end
U=U1;
%матрица А
A=U(1:n,1:m-1);
for i=1:n
A(i,i)=0;
end
%матрица B
B=-U(1:n,m);
%====================================================
%проверка 2
if rank(A) ~= rank(U)
error('Система не совместна');
end;
%вывод матриц
A
B
%сумма по строкам
norm1=zeros(n,1);
k=1;
for i=1:n
for j=1:m-1
norm1(k)=norm1(k)+abs(A(i,j));
end
if k<4
k=k+1;
end;
end
%матрица сумм по строкам
norm1;
%первая норма по строкам
max_norm1=max(norm1);
%сумма по столбцам
k=1;
norm2=zeros(n,1);
for j=1:m-1
for i=1:n
norm2(k)=norm2(k)+abs(A(i,j));
end
if k<4
k=k+1;
end
end
%матрица сумм по строкам
norm2;
%вторая норма по строкам
max_norm2=max(norm2);
%нахождение третьей нормы
%нахождение суммы элементов матрицы А
sum=0;
for i=1:n
for j=1:m-1
sum=sum+A(i,j)*A(i,j);
end
end
% третья норма
max_norm3=sqrt(sum);
%вывод значений норм матрицы А
max_norm1
max_norm2
max_norm3
%===================================================
%проверка условия сходимости метода итераций
if ( (max_norm1>1) && (max_norm2>1) && (max_norm3>1))
error('Введенная матрица не является диагонально преобладающей')
end;
%====================================================
%итерационный процесс
k=0;
X0=zeros(n,1);
X0=B;
X1=zeros(n,1);
for i=[1:n]
%нахождение суммы для Х1(i)
sum=0;
for j=[1:m-1]
sum = sum + ( A(i,j) * X0(j) );
end
X1(i)=sum + B(i);
end
while ( abs( X0(i) - X1(i) ) > eps )
X0=X1;
for i=[1:n]
%нахождение суммы для Х1(i)
sum=0;
for j=[1:m-1]
sum = sum + ( A(i,j) * X0(j) );
end
X1(i)=sum + B(i);
end
k=k+1;
end
%====================================================
%вывод вектора решений
X1
%вывод числа итераций для выполненияусловия точности
k
%=====================================================
return
ВСТРОЕННЫЕ ФУНКЦИИ ПАКЕТОВ MATHCAD И MATLAB
ДЛЯ ПРИБЛИЖЕННОГО РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Пакет MATHCAD
Решение систем линейных уравнений – довольно распространенная задача. Для системы линейных уравнений, заданной в матричном виде AX=B, вектор решения можно получить из очевидного выражения X=A-1B, или, например, из решения системы уравнений с проверкой на невырожденность матрицы:X:=if(|A|,A-1B,0).
Следует обратить внимание на то, что пакет содержит и встроенную функцию решения линейных систем lsolve(A,B), где А– матрица коэффициентов, а В – вектор свободных членов. Пример использования предложенных методов показан на рис. 5.1.
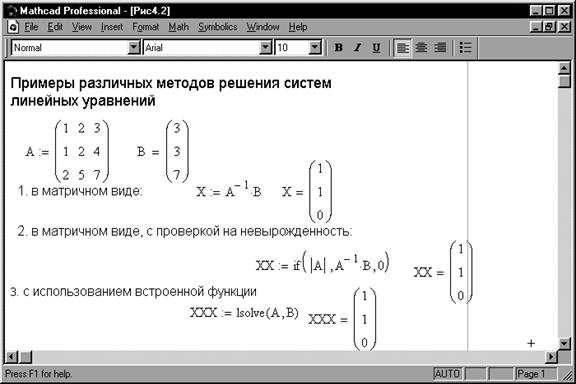
Рис. 5.1. Примеры решения системы
Для решения систем уравнений, систем неравенств, смешанных систем служат решающие блоки. Структура решающего блока:
начало | Given
тело | несколько конструкций вида АВ1 оп АВ2
(оп – некоторая операция отношения, причём для написания знака равенства используется особый «жирный» знак равенства, который находится на панели инструментов; знак присваивания в теле решающего блока не используется)
конец | FIND (список) или MINERR (список).
Список – это перечень переменных, которые необходимо найти.
С помощью FIND ищут точное решение; если оно отсутствует, то возникает ошибка. Посредством MINERR всегда будет найдено решение, минимизирующее невязку ограничений. Переменная ERR– величина ошибки.
Перед решающим блоком необходимо задать начальные условия для всех искомых переменных, можно в векторном виде. Соответственно, в теле решающего блока можно использовать запись уравнений в матричном виде. Максимальное количество уравнений в системе доведено до двухсот. Часто приходится решать системы уравнений при наличии определенных ограничений. Таким образом, в теле решающего блока могут быть одновременно как равенства, так и неравенства. Пример такой системы приведен ниже:
x:=1 y:=1
Given
x + y = 5
x + y = 2
x£1
y>2
find (x,y) =
Для последующего использования результатов необходимо так организовать конец:
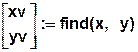
В теле решающего блока нельзя строить графики, выполнять вычисления.
Итерации производятся до тех пор, пока ôERRô£ TOL. Если встречается седловая точка и не известно, куда направлен градиент, то выдается сообщение not converging (не решаемо). Количество итераций ограничено. Возможно сообщение об ошибке вида did not find solution (не найдено решение).
При возникновении таких ошибок можно:
– изменить точность – TOL;
– заменить начальные условия;
– заменить find на minerr и получить приближенное решение.
Однако при использовании функций findи minerrнужно проявлять осторожность и обязательно предусматривать проверку решений, т.к. нередки случаи, когда решение может оказаться ошибочным.
Для получения другого решения можно поменять начальные условия, для уточнения – уменьшить TOL.
Пакет MATLAB
Рассмотрим две системы линейных уравнений: АХ=В и ХА=В. В MATLAB такие системы решаются без вычисления обратной матрицы. Два типа матричного деления / и \ используются для этих двух ситуаций, когда неизвестная матрица стоит слева или справа от матрицы коэффициентов:
Х=А\В соответствует решению АХ=В;
Х=В/А соответствует решению ХА = В.
При этом должны выполняться условия соответствия размерностей матриц X, А, В. Напомним, что для варианта Х=А\В матрица X должна иметь то же количество столбцов, что и матрица В, и то же число строк, сколько столбцов у матрицы А. Для Х=В/А эти условия обратны.
Алгебраические свойства оператора / можно вывести из соотношения(В/А)' = (А'\В’).
Матрица не обязательно должна быть квадратной, она может быть размером mхn. При этом существуют следующие варианты:
· m = n – квадратная система, возможно нахождение точного решения;
· m > n – переопределенная система, решение ищется с помощью метода наименьших квадратов;
· m < n – недоопределенная система, ищется базовое решение.
Пример решения и проверки результатов для квадратной системы:
<<А = раscal(З), В = magic(3)
А =
1 1 1
1 2 3
1 3 6
В =
8 1 6
3 5 7
4 9 2
<< Х=А\В
X =
19 -3 -1
-17 4 13
6 0 -6
<< % проверка эквивалентности
<< А*Х==В
ans =
1 1 1
1 1 1
1 1 1
Важно помнить, что система имеет единственное решение, если detА не равен нулю, иначе решение либо не существует, либо не единственно. Отметим также, что для нахождения обратной матрицы используется функция inv(А).
Для решения системы АХ=В можно записать Х=inv(А)*B, а для решения системы Х=В/А– Х=В*inv(А), однако операторы \,/ работают быстрее.
Для прямоугольных матриц детерминант и обратная матрица не определены, но можно найти псевдообратную матрицу, то есть матрицу, для которой выполняется хотя бы одно из соотношений: АХ=I или ХА = I. Для этого имеется функция рinv(А).
Если А – матрица размером mхnи m>n и ранг матрицы равен n, то каждое из трех следующих выражений вычисляет X по методу наименьших квадратов:
Х=А\В
Х=рinv(А)*В
Х=inv(А'*А)*А'*В
В противном случае решение Xпо методу наименьших квадратов не единственно и существует множество векторов, минимизирующих norm(A*X-B).Решение, вычисленное с помощью Х=А\В,– базовое решение, имеющее не больше r ненулевых компонент: r=rank(A). Решение, вычисленное с помощью Х=рinv(А)*В,– это решение с минимальной нормой X.
