Задания к практической работе № 5

Практическая работа № 5

По дисциплине «Математика»

для студентов очно – заочного отделения

Тема: Полное исследованию функции и построение графика .

Цель: Научиться исследовать функцию с помощью нахождения производных; строить график

Функции по ее свойствам.

Перечень необходимых сведений из теории:

1. Экстремуму функций: необходимое и достаточное условие.

2. Нахождение экстремумов с помощью второй производной.

3. Точки перегиба графика функции.

4. Асимптоты графика функции.

5. Полное исследование фикции и построение графика функции.

Порядок выполнения работы:

1. Повторите теоретический материал данной темы Ознакомьтесь с образцом выполнения задания.

2. Ознакомьтесь с заданием своего варианта и выполните задание.

3. Оформите практическую работу в соответствии с требованиями, указанными в методике проведения практических работ ( п.2 данного пособия)

Образец выполнения задания:

Задание: Проведите полное исследование функции 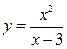и постройте ее график.

Решение:

1. Находим область определения функции: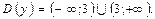

2. Данная функция не является ни четной, ни нечетной, ни периодической.

3. При х=0 получим у=0, т.е. график проходит через начало координат.

4. Так как 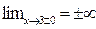, то прямая х=3 служит вертикальной асимптотой графика. Далее находим :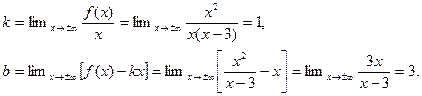

Следовательно, прямая у=х+3 является наклонной асимптотой графика.

5. Находим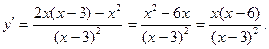

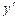Производная обращается в нуль в точках х=0 и х=6 и терпит разрыв при х=3. Этими точками числовая прямая делится на четыре промежутка : 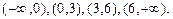Исследуем знак 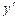в каждом из них; очевидно, что 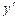>0 в промежутках 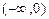и 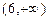( в этих промежутках функция возрастает) и 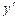<0 в промежутках (0,3) и (3,6) ( в этих промежутках функция убывает). При переходе через точку х=0 производная меняет знак с плюса на минус, т.е. это точка максимума, а при переходе через точку х=6 – с минуса на плюс, т.е. это точка минимума. Находим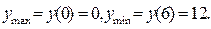

6. Находим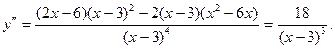

Вторая производная в нуль нигде не обращается и терпит разрыв при х=3. В промежутке 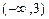имеем 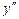<0, т.е. в этом промежутке кривая выпукла вверх; в промежутке 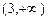имеем 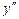>0, т.е. в этом промежутке кривая выпукла вниз. Точек перегиба нет.

7. На основании полученных данных составляем таблицу :

	+		-		-		+
	-		-		+		+
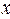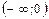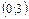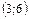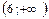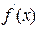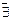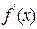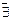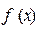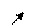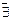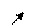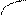		max		разрыв		min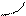

8. Строим график функции, начиная с построения асимптот:

9.

y

0 6 x

Задания к практической работе № 5

Задание: Проведите полное исследование функции 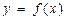и постройте ее график.

Исходные данные по вариантам

№ вари анта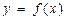

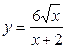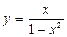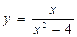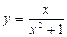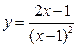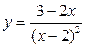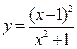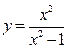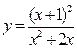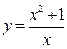В результате выполнения практической работы студент должен:

знать:

- экстремуму функций: необходимое и достаточное условие.

- точки перегиба графика функции.

- асимптоты графика функции.

уметь:

- определять область определения и множество значений функции;

- исследовать функцию на четность и периодичность;

- находить точки пересечения графика функции с осями координат;

- находить асимптоты графика функции;

- находить точки экстремума функции;

- находить промежутки монотонности функции с помощью первой производной;

- находить точки перегиба графика функции с помощью второй производной;

- строить график функции.