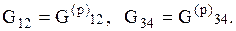Составитель- профессор, д.т.н. Шаймарданов Р.Г.
Современные методы расчета химико-технологических систем
Методические указания и контрольное задание
Составитель- профессор, д.т.н. Шаймарданов Р.Г.
Бугульма, 2016
СОВРЕМЕННЫЕ МЕТОДЫ РАСЧЕТА ХИМИКО-ТЕХНОЛОГИЧЕСКИХ СИСТЕМ С МАТЕРИАЛЬНЫМИ И ТЕПЛОВЫМИ РЕЦИКЛАМИ Методические указания . В методических указаниях рассматриваются вопросы, связанные с расчетом химико-технологических систем (ХТС) с материальными и тепловыми рециклами. Приведены алгоритмы решения задач, которые предполагают при расчетах использовать электронную таблицу EXCEL и систему компьютерной математики Mathcad. Методические указания соответствуют содержанию дисциплине «Современные методы расчета ХТС» государственных образовательных стандартов. ВВЕДЕНИЕ В методических указаниях приводятся известные методы расчета ХТС с материальными и тепловыми рециклами, что позволяет прогнозировать поведение сложных процессов в изменяющихся условиях функционирования систем. Методические указания состоят из четырех разделов: первый раздел- теоретический, второй - представляет собой варианты расчетных контрольных работ, третий - приложение содержит необходимые сведения по расчету ХТС с использованием электронной таблицы EXCEL, четвертый раздел содержит контрольные задания. В первой главе Раздела 1 методических указаний рассматриваются итерационные методы для решения уравнений на местах разрыва потоков. Во второй главе рассматривается метод простой итерации для расчета ХТС. В третьей главе рассматривается метод Вегстейна для расчета ХТС. В четвертой главе приводится пример декомпозиционного расчета ХТС с использованием простой итерации, электронной таблицы EXCEL и системы компьютерной математики Mathcad. В Разделе 2 предлагаются варианты контрольных работ для расчета ХТС. Раздел 3 – как приложение содержит необходимые сведения по расчету ХТС с использованием электронной таблицы EXCEL. Раздел 4 содержит варианты к контрольному заданию и перечень контрольных вопросов. При использовании методических указаний целесообразно сначала обратиться к вводным материалам, которые содержатся в главах 1-4 Раздела 1 и затем перейти к Разделу 2,3 для выполнения самостоятельной работы по расчету ХТС и в последующем – к выполнению контрольного задания, изложенного в Разделе 4. РАЗДЕЛ 1 1 ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ НА МЕСТАХ РАЗРЫВОВ Декомпозиционный метод предполагает решение уравнений на местах разрыва потоков. При этом могут быть использованы традиционные методы решения систем нелинейных алгебраических уравнений. Как известно, в результате структурного анализа ХТС комплекс превращается в разомкнутую систему (рисунок 1.1). На месте разрыва необходимо решать систему уравнений в неявном виде: X = Y ( X ) 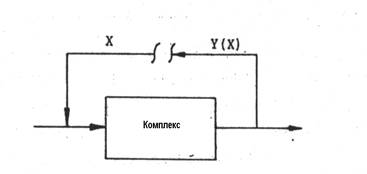 Рисунок 1.1 – Представление комплекса после разрыва потоков Рисунок 1.1 – Представление комплекса после разрыва потоков 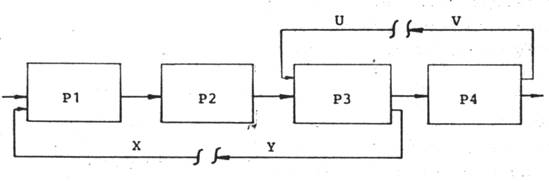 Рисунок 1.2 - Представление комплекса после разрыва потоков На местах разрыва потоков (рисунок 1.2) необходимо решать уравнения: U = V ( U , X ) Y = X ( U , X ) Для решения этих уравнений в современных программных продуктах используются следующие методы: · метод простой итерации, · метод Вегстейна, · метод Ньютона-Рафсона Рисунок 1.2 - Представление комплекса после разрыва потоков На местах разрыва потоков (рисунок 1.2) необходимо решать уравнения: U = V ( U , X ) Y = X ( U , X ) Для решения этих уравнений в современных программных продуктах используются следующие методы: · метод простой итерации, · метод Вегстейна, · метод Ньютона-Рафсона  и другие. В общем случае на местах разрыва необходимо решать следующую систему из и другие. В общем случае на местах разрыва необходимо решать следующую систему из 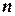 нелинейных алгебраических уравнений с нелинейных алгебраических уравнений с 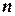 неизвестными: неизвестными: 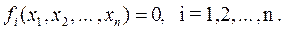 2 МЕТОД ПРОСТОЙ ИТЕРАЦИИ И ЕГО МОДИФИКАЦИИ Для применения метода простой итерации система рассматриваемых уравнений преобразуется к следующему виду: 2 МЕТОД ПРОСТОЙ ИТЕРАЦИИ И ЕГО МОДИФИКАЦИИ Для применения метода простой итерации система рассматриваемых уравнений преобразуется к следующему виду: 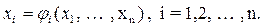 Задаются начальные приближения и осуществляется поиск решения по этому преобразованному уравнению. Необходимо отметить, что на сходимость процедуры поиска решения сильно влияет способ представления преобразованных уравнений и выбор начального приближения. Пример 1. Рассмотрим решение уравнения Задаются начальные приближения и осуществляется поиск решения по этому преобразованному уравнению. Необходимо отметить, что на сходимость процедуры поиска решения сильно влияет способ представления преобразованных уравнений и выбор начального приближения. Пример 1. Рассмотрим решение уравнения 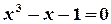 (1) Начальное приближение (1) Начальное приближение 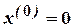 , точность решения , точность решения 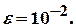 Представим уравнение в виде: Представим уравнение в виде: 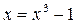 (2) Результаты, приведенные в таблице 2.1, показывают, что процесс решения расходится. Таблица 2.1 – Результаты решения уравнения (2) методом простой итерации (2) Результаты, приведенные в таблице 2.1, показывают, что процесс решения расходится. Таблица 2.1 – Результаты решения уравнения (2) методом простой итерации
Представим уравнение (1) в виде: Результаты, приведенные в таблице, показывают, что процесс решения сходится. Таблица 2.2 - Результаты решения уравнения (3) методом простой итерации
На 4 шаге выполняется условие сходимости Пример 2. Рассмотрим решение системы уравнений:
Начальное приближение Представим систему в виде (5)
В таблице 2.3 показан ход итерационного процесса поиска решения системы (4). Таблица 2.3- ход итерационного процесса
3 МЕТОД ВЕГСТЕЙНА В соответствии с этим методом: где В нижеследующей таблице приведены результаты решения системы (4) с использованием метода Вегстейна.
4 ПРИМЕР ДЕКОМПОЗИЦИОНННОГО РАСЧЕТА ХТС С
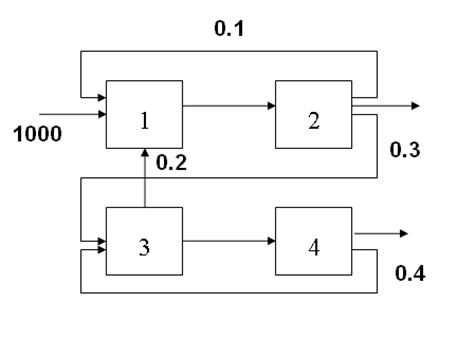
Определить расходы промежуточных и выходных потоков ХТС (см.рисунок 4.1). Пусть
Рисунок 4.1- Химико-технологическая система Здесь и в дальнейшем приняты следующие обозначения: 4.1 СТРУКТУРНЫЙ АНАЛИЗ ХТС Все элементы ХТС образуют комплекс, т. е. могут быть рассчитаны только совместно. В соответствии со структурным анализом ХТС с помощью прадерева можно выделить следующие контуры:
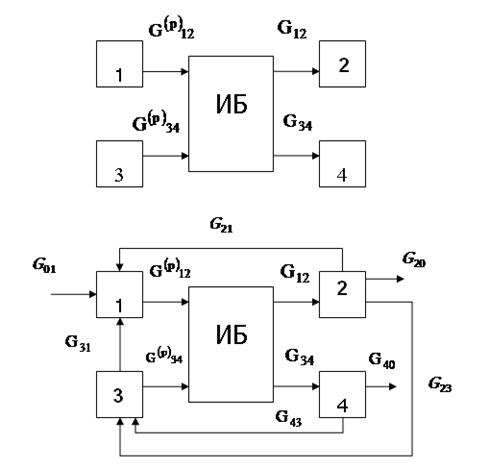
Так как параметричность всех потоков одинакова (каждый поток характеризуется только расходом), то для преобразования замкнутой ХТС в разомкнутую можно воспользоваться, например, разрывом дуг 1—2 и 3—4. Окончательная последовательность расчета ХТС: {ИБ, 2, 4, 3, 1},где ИБ-итерационный блок, в котором задаются начальные приближения по потокам, и обеспечивается равенство параметров полученных потоков. Информационная блок-схема расчета ХТС с указанием расходов соответствующих потоков представлена на рисунке 4.2.
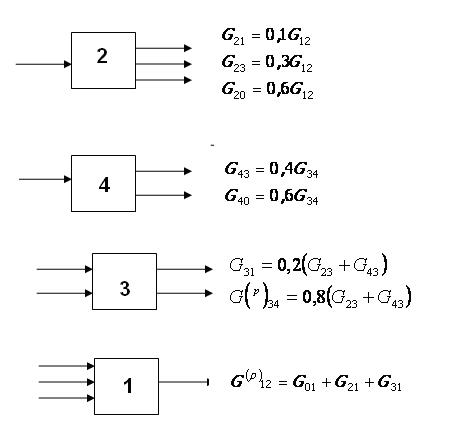
Рисунок 4.2- Этапы составления информационной блок-схемы 4.2 СОСТАВЛЕНИЕ МАТЕМАТИЧЕСКИХ ОПИСАНИЙ ЭЛЕМЕНТОВ ХТС Для расчета ХТС необходимо наличие математических описаний отдельных элементов ХТС. В рассматриваемом примере их можно составить с помощью соотношений между расходами потоков, заданных в условии. Запишем математические описания элементов ХТС согласно определенной ранее вычислительной последовательности ( см.рисунок 4.3). На рисунке 4.3 В результате расчета должно быть: Таким образом, математическое описание данной ХТС представляет собой систему из 8-и линейных уравнений с 8-ю неизвестными. Для данного примера конечно можно воспользоваться известными методами решения таких уравнений. В общем же случае, как правило, получается система нелинейных уравнений. Для решения данной задачи можно воспользоваться различными методами, в данном случае - методом простой итерации. Этот метод носит общий характер и с успехом применяется для расчета сложных реальных ХТС.
Рисунок 4.3 - Последовательность расчета элементов ХТС |
Алгоритм решения задачи
Шаг 1. Ввод исходных данных.
В данном случае таковыми будут:
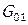 — расход входного потока, кг·ч-1 ;
— расход входного потока, кг·ч-1 ;
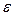 — точность вычисления, %;
— точность вычисления, %;
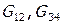 — начальные приближения для расходов на выходе ИБ.
— начальные приближения для расходов на выходе ИБ.
Шаг 2. Задание номера итерации, k =1.
Шаг 3. Расчет ХТС в соответствии с найденной в результате структурного анализа последовательностью:
сначала необходимо для элемента 2 определить значения расходов для выходных потоков 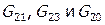 ,
,
затем — для элемента 4: 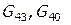 ,
,
далее для элемента 3: 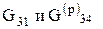
и, наконец, для элемента 1 значение 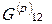 . Индекс р указывает на расчетные значения
. Индекс р указывает на расчетные значения
Шаг 4. Проверка условий
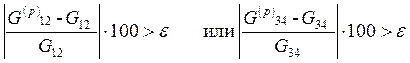
Шаг 5. Если эти условия выполнены, т. е. значения соответствующих расходов на местах разрывов определены с большей погрешностью, чем 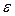 , то в соответствии с методом простой итерации
, то в соответствии с методом простой итерации
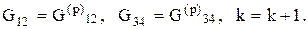
и вычисления ХТС повторяются, начиная с шага 3.
Шаг 6. Если же условия не выполнены, т. е. значения соответствующих расходов на местах разрыва найдены с заданной точностью, то выполняется шаг 7.
Шаг 7. Печать числа итераций k , необходимых для расчета ХТС, и значений расходов промежуточных и выходных потоков.
По приведенному выше алгоритму была составлена программа для реализации задачи с помощью электронной таблицы Excel и системы компьютерной математики Mathcad.
4.3 РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ ЭЛЕКТРОННОЙ ТАБЛИЦЫ EXCEL

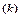
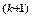
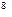
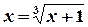 (3)
(3)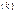
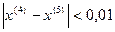 и итерационный процесс заканчивается.
и итерационный процесс заканчивается.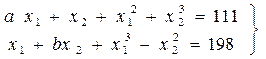 (4)
(4)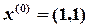 , при a = 100, b = 100.
, при a = 100, b = 100.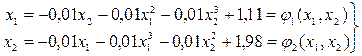 (5)
(5)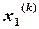
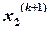
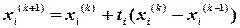 ,
,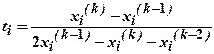
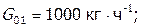
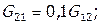
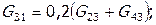
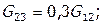
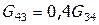 .
.
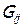 - расход потока, выходящего из i -го элемента и поступающего в j - й элемент. Если первый индекс 0, то поток соответствует входному потоку ХТС, если второй индекс 0, поток соответствует выходному потоку ХТС.
- расход потока, выходящего из i -го элемента и поступающего в j - й элемент. Если первый индекс 0, то поток соответствует входному потоку ХТС, если второй индекс 0, поток соответствует выходному потоку ХТС.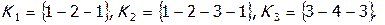
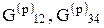 - рассчитанные расходы соответствующих разорванных потоков. Их начальные значения задаются в виде приближенных значений
- рассчитанные расходы соответствующих разорванных потоков. Их начальные значения задаются в виде приближенных значений