Пусть заданы векторы в прямоугольной системе координат
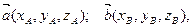 тогда линейные операции над ними в координатах имеют вид:
тогда линейные операции над ними в координатах имеют вид:
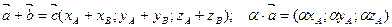
Скалярное произведение векторов.
Определение. Скалярным произведениемвекторов  и
и  называется число, равное произведению длин этих сторон на косинус угла между ними.
называется число, равное произведению длин этих сторон на косинус угла между ними.

 ×
×  = ï
= ï  ïï
ïï  ïcosj
ïcosj
Свойства скалярного произведения:
1)  ×
×  = ï
= ï  ï2;
ï2;
2)  ×
×  = 0, если
= 0, если  ^
^  или
или  = 0 или
= 0 или  = 0.
= 0.
3)  ×
×  =
=  ×
×  ;
;
4)  ×(
×(  +
+ 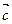 ) =
) =  ×
×  +
+  ×
× 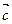 ;
;
5) (m  )×
)×  =
=  ×(m
×(m  ) = m(
) = m(  ×
×  ); m=const
); m=const
Если рассматривать векторы 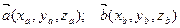 в декартовой прямоугольной системе координат, то
в декартовой прямоугольной системе координат, то

 ×
×  = xa xb + ya yb + za zb;
= xa xb + ya yb + za zb;
Используя полученные равенства, получаем формулу для вычисления угла между векторами:

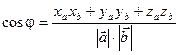 ;
;
Пример. Найти (5  + 3
+ 3  )(2
)(2  -
-  ), если
), если 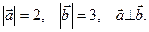
10  ×
×  - 5
- 5  ×
×  + 6
+ 6  ×
×  - 3
- 3  ×
×  = 10
= 10 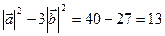 ,
,
т.к. 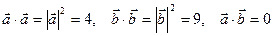 .
.
Пример. Найти угол между векторами  и
и  , если
, если 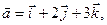
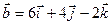 .
.
Т.е.  = (1, 2, 3),
= (1, 2, 3),  = (6, 4, -2)
= (6, 4, -2)
 ×
×  = 6 + 8 – 6 = 8:
= 6 + 8 – 6 = 8:
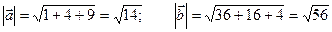 .
.
cosj = 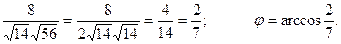
Пример. Найти скалярное произведение (3  - 2
- 2  )×(5
)×(5  - 6
- 6  ), если
), если 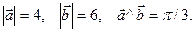
15  ×
×  - 18
- 18  ×
×  - 10
- 10  ×
×  + 12
+ 12  ×
×  = 15
= 15 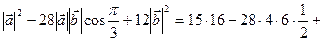
+ 12×36 = 240 – 336 + 432 = 672 – 336 = 336.
Пример. Найти угол между векторами  и
и  , если
, если 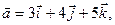
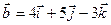 .
.
Т.е.  = (3, 4, 5),
= (3, 4, 5),  = (4, 5, -3)
= (4, 5, -3)
 ×
×  = 12 + 20 - 15 =17 :
= 12 + 20 - 15 =17 :
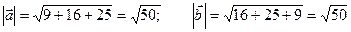 .
.
cosj = 
Пример. При каком m векторы 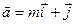 и
и 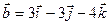 перпендикулярны.
перпендикулярны.
 = (m, 1, 0);
= (m, 1, 0);  = (3, -3, -4)
= (3, -3, -4)
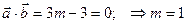 .
.
Пример. Найти скалярное произведение векторов 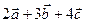 и
и 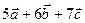 , если
, если 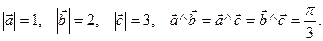
( 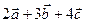 )(
)( 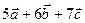 ) =
) = 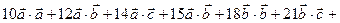
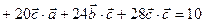
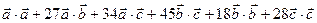 = 10 +
= 10 +
+ 27 + 51 + 135 + 72 + 252 = 547.
Векторное произведение векторов.
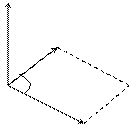
Определение. Векторным произведениемвекторов  и
и  называется вектор
называется вектор 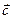 , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
1) 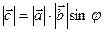 , где j - угол между векторами
, где j - угол между векторами  и
и  ,
,
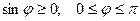
2) вектор 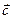 ортогонален векторам
ортогонален векторам  и
и 
3)  ,
,  и
и 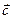 образуют правую тройку векторов.
образуют правую тройку векторов.
Обозначается: 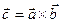 или
или 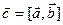 .
.
 |
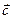

j

Свойства векторного произведения векторов:
1) 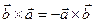 ;
;
2) 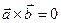 , если
, если  ïï
ïï  или
или  = 0 или
= 0 или  = 0;
= 0;
3) (m  )´
)´  =
=  ´(m
´(m  ) = m(
) = m(  ´
´  );
);
4)  ´(
´(  +
+ 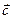 ) =
) =  ´
´  +
+  ´
´ 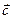 ;
;
5) Если заданы векторы  (xa, ya, za) и
(xa, ya, za) и  (xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами
(xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами 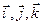 , то
, то

 ´
´  =
= 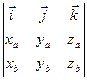
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах  и
и  .
.
Пример. Найти векторное произведение векторов 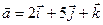 и
и
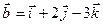 .
.
 = (2, 5, 1);
= (2, 5, 1);  = (1, 2, -3)
= (1, 2, -3)
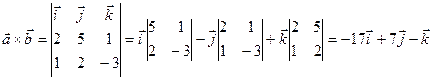 .
.
При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая может найти скалярное и векторное произведения двух векторов. Для запуска программы дважды щелкните на значке:
 |
В открывшемся окне программы введите координаты векторов и нажмите Enter. После получения скалярного произведения нажмите Enter еще раз – будет получено векторное произведение.
Примечание: Для запуска программы необходимо чтобы на компьютере была установлена программа Maple (Ó Waterloo Maple Inc.) любой версии, начиная с MapleV Release 4.
Пример. Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3),
С(0, 1, 0).
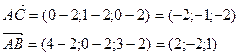
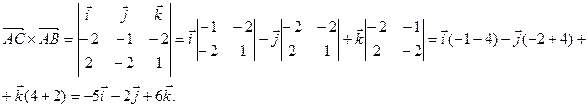
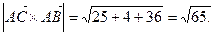
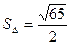 (ед2).
(ед2).
Пример. Доказать, что векторы 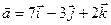 ,
, 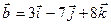 и
и 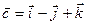 компланарны.
компланарны.
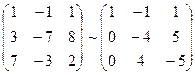 , т.к. векторы линейно зависимы, то они компланарны.
, т.к. векторы линейно зависимы, то они компланарны.
Пример. Найти площадь параллелограмма, построенного на векторах 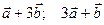 , если
, если 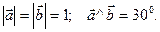
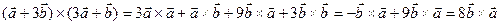
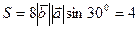 (ед2).
(ед2).
Смешанное произведение векторов.
Определение. Смешанным произведением векторов  ,
,  и
и 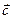 называется число, равное скалярному произведению вектора
называется число, равное скалярному произведению вектора  на вектор, равный векторному произведению векторов
на вектор, равный векторному произведению векторов  и
и 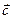 .
.
Обозначается 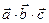 или (
или (  ,
,  ,
, 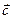 ).
).
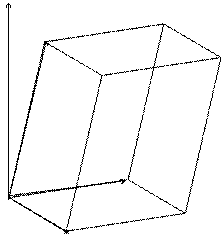
Смешанное произведение 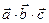 по модулю равно объему параллелепипеда, построенного на векторах
по модулю равно объему параллелепипеда, построенного на векторах  ,
,  и
и 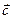 .
.
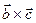

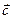

Свойствасмешанного произведения:
1)Смешанное произведение равно нулю, если:
а) хоть один из векторов равен нулю;
б) два из векторов коллинеарны;
в) векторы компланарны.
2) 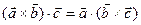
3) 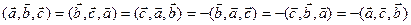
4) 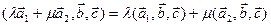
5) Объем треугольной пирамиды, образованной векторами  ,
,  и
и 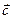 , равен
, равен
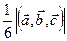
6)Если 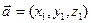 ,
, 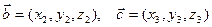 , то
, то
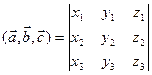
Пример. Доказать, что точки А(5; 7; 2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) лежат в одной плоскости.
Найдем координаты векторов: 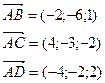
Найдем смешанное произведение полученных векторов:
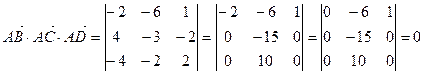 ,
,
Таким образом, полученные выше векторы компланарны, следовательно точки A, B, C и D лежат в одной плоскости.
Пример. Найти объем пирамиды и длину высоты, опущенной на грань BCD, если вершины имеют координаты A(0; 0; 1), B(2; 3; 5), C(6; 2; 3), D(3; 7; 2).
Найдем координаты векторов: 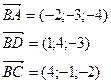
Объем пирамиды 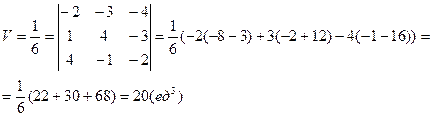
Для нахождения длины высоты пирамиды найдем сначала площадь основания BCD.
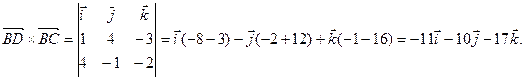
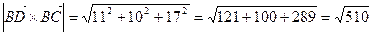
Sосн = 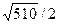 (ед2)
(ед2)
Т.к. V = 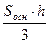 ;
; 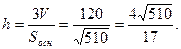 (ед)
(ед)
Уравнение поверхности в пространстве.
Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
Общее уравнение плоскости.
Определение. Плоскостьюназывается поверхность, все точки которой удовлетворяют общему уравнению:

Ax + By + Cz + D = 0,
где А, В, С – координаты вектора 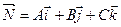 -вектор нормали к плоскости.
-вектор нормали к плоскости.
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох
В = 0 – плоскость параллельна оси Оу
С = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
Уравнение плоскости, проходящей через три точки.
