Равенство (5.4) называется основной теоремой зацепления.
Нормаль в точке соприкосновения элементов высшей пары качения и скольжения делит линию центров на части. Обратно пропорциональные угловым скоростям.
Точка 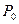 , делящая линию центров
, делящая линию центров  на части. Обратно пропорционально угловым скоростям, является мгновенным центром вращения в относительном движении звеньев 1 и 2.
на части. Обратно пропорционально угловым скоростям, является мгновенным центром вращения в относительном движении звеньев 1 и 2.
Расстояние a между точками  и
и  равно
равно
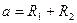
 (5.5)
(5.5)
Из равенства (5.4) и (5.5) следует, что радиусы 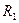 и
и 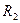 центроид равны
центроид равны
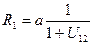 , и
, и 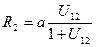 (5.6)
(5.6)
Мгновенный центр вращения 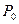 в теории зацеплений называется полюсом зацепления.
в теории зацеплений называется полюсом зацепления.
При переменном значении передаточной функции  полюс зацепления
полюс зацепления 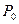 занимает на линии центров
занимает на линии центров 
 переменные положения. При постоянном значении
переменные положения. При постоянном значении  полюс зацепления располагается в одной и той же точке на прямой
полюс зацепления располагается в одной и той же точке на прямой  .
.
Если угловые скорости 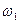 и
и 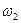 имеют разные знаки (см. рис 5.1,a), то
имеют разные знаки (см. рис 5.1,a), то 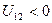 и полюс зацепления
и полюс зацепления 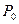 лежит между точками
лежит между точками  и
и  . Этот вид зацепления называется внешним. Если
. Этот вид зацепления называется внешним. Если 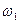 и
и 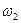 имеют одинаковый знак и полюс зацепления
имеют одинаковый знак и полюс зацепления 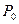 лежит вне отрезка
лежит вне отрезка  , то
, то 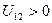
 (зацепление внутреннее).
(зацепление внутреннее).
Основной закон зацепления формулируется так: для сохранения постоянства передаточного отношения зубчатого механизма необходимо, чтобы нормаль к зацепляющимся профилям зубьев в точке контакта всегда проходила на линии центров через одну и ту же точку 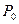 (полюс зацепления).
(полюс зацепления).
5.2. Эвольвента окружности. Её уравнение и свойства
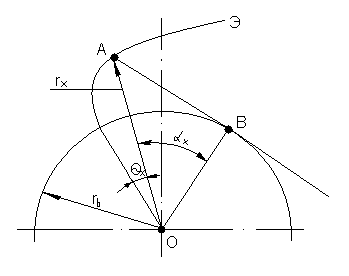
Рис.5.2. К образованию эвольвентного профиля зуба.
Если по окружности перекатывается без скольжения прямая AB (рис.5.2) то любая точка этой прямой описывает эвольвенту Э, часть которой принимается в качестве кривой, очерчивающей рабочую часть профиля зуба. Окружность радиуса 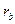 , развёртка которой является эвольвентой, называется основной.
, развёртка которой является эвольвентой, называется основной.
Так как точка В прямой АВ является мгновенным центром вращения, то отрезок ВА является радиусом кривизны эвольвенты в т. А. Угол давления 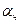 , образованный радиус-вектором
, образованный радиус-вектором 
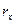 и перпендикуляром ОВ, можно найти по зависимости
и перпендикуляром ОВ, можно найти по зависимости 
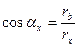 . Угол
. Угол 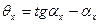 называется эвольвентной функцией и обозначается
называется эвольвентной функцией и обозначается 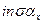 .
. 
Если основную окружность заменить основным цилиндром с радиусом 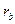 , а прямую АВ плоскостью Н, то при обкатке её без скольжения по основному цилиндру прямая
, а прямую АВ плоскостью Н, то при обкатке её без скольжения по основному цилиндру прямая 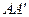 , параллельная образующей основного цилиндра
, параллельная образующей основного цилиндра 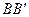 , опишет эвольвентную поверхность прямого зуба. Если на плоскости Н взять прямую
, опишет эвольвентную поверхность прямого зуба. Если на плоскости Н взять прямую 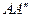 , расположенную под углом
, расположенную под углом 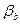 к образующей основного цилиндра, то при обкатке плоскости Н эта прямая образует винтовую поверхность, которая используется в качестве рабочей поверхности зуба косозубого колеса.
к образующей основного цилиндра, то при обкатке плоскости Н эта прямая образует винтовую поверхность, которая используется в качестве рабочей поверхности зуба косозубого колеса.
В торцовом сечении косого зуба – сечении перпендикулярном к оси колеса,- профиль зуба будет эвольвентным. Все размеры, характеризующие зацепление в этом сечении, снабжаются индексом t( 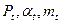 и т.д.). Параметры зацепления в нормальном сечении плоскостью, перпендикулярной к направлению зуба, характеризующему углом наклона зубьев
и т.д.). Параметры зацепления в нормальном сечении плоскостью, перпендикулярной к направлению зуба, характеризующему углом наклона зубьев 
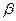 , снабжаются индексом n (
, снабжаются индексом n ( 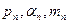 и т.д.). Боковые поверхности зубьев конических колёс образуются подобно эвольвентными цилиндрическими, но вместо основного цилиндра образующая плоскость обкатывается по основному конусу. Если прямую
и т.д.). Боковые поверхности зубьев конических колёс образуются подобно эвольвентными цилиндрическими, но вместо основного цилиндра образующая плоскость обкатывается по основному конусу. Если прямую 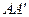 заменить любой другой прямой или кривой на плоскости Н, то получим боковую поверхность непрямого зуба (косого, кругового и др.) конического колеса.
заменить любой другой прямой или кривой на плоскости Н, то получим боковую поверхность непрямого зуба (косого, кругового и др.) конического колеса.
