Iii. применения производной
I. Таблица производных
1. 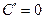 , где С – const;
, где С – const;
2. 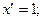
3. 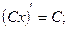
4. 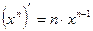 ;
;
5. 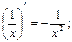
6. 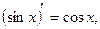 7.
7. 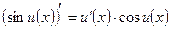 ;
;
8. 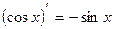 ; 9.
; 9. 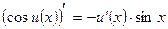 ;
;
10. 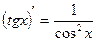 ; 11.
; 11. 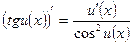 ;
;
12. 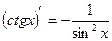 ; 13.
; 13. 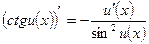 ;
;
14. 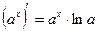 ; 15.
; 15. 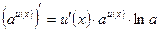 ;
;
16. 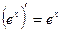 ; 17.
; 17. 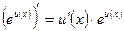 ;
;
18. 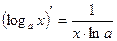 ; 19.
; 19. 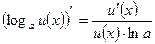 ;
;
20. 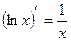 ; 21.
; 21. 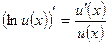 .
.
Правила дифференцирования
I. 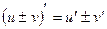 , где
, где 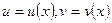 ;
;
II. 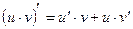 , где
, где 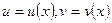 ;
;
III. 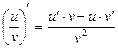 , где
, где 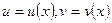 ;
;
IV. 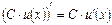 ;
;
V. 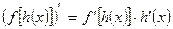 ;
;
II. ПРАВИЛА ВЫЧИСЛЕНИЯ ПРОИЗВОДНОЙ
(§4, п15-17)
Рассмотрим применение основных правил дифференцирования и применение таблицы производных при решении задач.
Пример . Вычислить производную:
а) 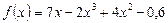 ; б)
; б) 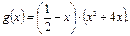 ;
;
в) 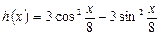 ; г)
; г)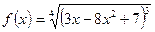 ;
;
д) 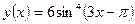 ; е)
; е) 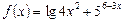 ;
;
ж) 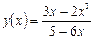 .
.
РЕШЕНИЯ
а)Вычислить производную: 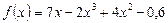 ;
;
Решение:
Так как производная суммы нескольких слагаемых равна сумме производных от этих слагаемых (см.правило I), то получим:
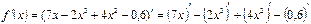
Постоянный множитель можно выносить за знак производной (см.правило №4):
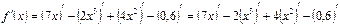
Применяя последовательно формулы под номерами 3, 4 и 1 в таблице производных, получим:
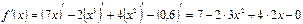 =
= 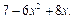
Ответ: 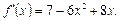
б) Вычислить производную: 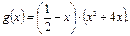
Решение:
Так как функция g(x) представляет собой произведение, то необходимо применить правило дифференцирования произведения (формула №II).
В данном примере 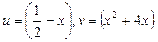
Подставляя данные значения в правую часть формулы №II, получим:
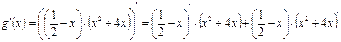 ;
;
Теперь необходимо вычислить значения производной первого и последнего сомножителей. Применяя к ним последовательно правило дифференцирования I и формулы № 1, 2, 4, 3 из таблицы производных, имеем:
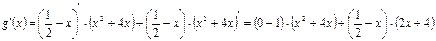
Раскроем скобки и приведем подобные члены:
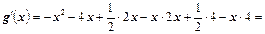
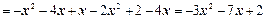
Ответ: 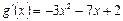 .
.
в) Вычислить производную 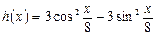
Решение:
Прежде чем дифференцировать данную функцию, упростим ее, для этого вынесем общий множитель за скобку, а выражение, стоящее в скобке свернем по формуле косинуса двойного угла, то есть, применим формулу 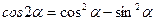 , получим:
, получим:
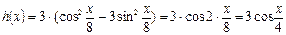
Применяя последовательно формулы 9, 14, 3, имеем:
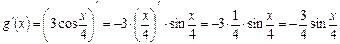 .
.
Ответ: 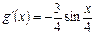 .
.
г). Вычислить производную: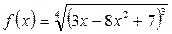
Решение:
Применяя формулу 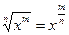 преобразуем данное выражение:
преобразуем данное выражение:
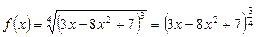 .
.
Применяя правило дифференцирования сложной функции (правило V), получим:
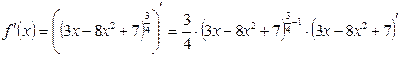 Учитывая, что
Учитывая, что 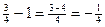 и применяя к последней скобке правило дифференцирования I, а затем последовательно формулы №3, 4 и 1, имеем:
и применяя к последней скобке правило дифференцирования I, а затем последовательно формулы №3, 4 и 1, имеем:
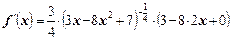
Преобразовывая степенное выражение по формуле 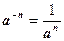 , и учитывая, что
, и учитывая, что 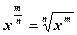 получим:
получим:
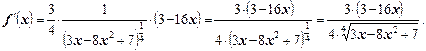
Ответ: 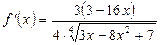 .
.
д) Вычислить производную: 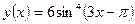
Решение:
Для нахождения производной данной функции необходимо вынести постоянный множитель (т.е.число 6) вынести за знак производной (правило дифференцирования IV) и применить правило дифференцирования сложной функции (формула V):
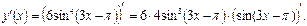
Производная выражения, стоящего в скобке, находится по формуле №7 (см. таблицу производных):
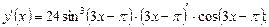
Раскрывая последнюю производную по правилу дифференцирования I, применяя формулы №,3 и 1 из таблицы производных и перемножая коэффициенты, получим:
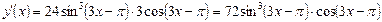
Ответ: 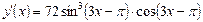
е) Вычислить производную: 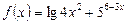
Решение:
Данная функция представляет собой сумму двух функций, зависящих от х, поэтому производная функции равна сумме производных от каждого слагаемого (применяется правило дифференцирования I).
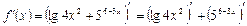
Каждое слагаемое представляет собой сложную функцию, поэтому для нахождения производной последовательно применяем формулы 19 и 15, имеем:
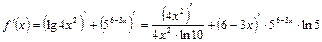
Раскрывая производную числителя по формуле 4, а производную скобки по правилу дифференцирования I и формулам 1 и 3 (см таблицу производных), после сокращения дроби на выражение 4х, получим:
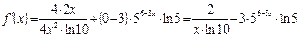
Ответ: 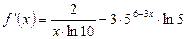
ж) Вычислить производную: 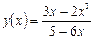
Решение:
Так как исходная функция представляет собой дробное выражение, то для нахождения ее производной необходимо применить правило дифференцирования дроби, т.е. правило III. Учитывая, что в данном примере
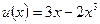 ,
,
а 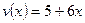 ,
,
получим:
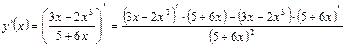 ;
;
Для вычисления производной первой и последней скобок, стоящих в числителе, необходимо сначала применить правило дифференцирования I, а затем последовательно формулы 3, 4 1 и 3.
В результате получим:
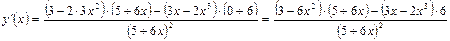
Раскрывая скобки и приводя подобные члены, получим значение производной исходной функции:
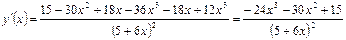
Ответ: 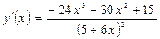
III. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ
