Викладач:доцент Воробйова А.І
Чорноморський державний університет ім. Петра Могили
Кафедра прикладної та вищої математики
Індивідуальне завдання № 2.2.1 та 2.2.2
Методичні вказівки
З вищої математики
Тема: Диференціювання.
Викладач:доцент Воробйова А.І.
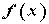
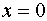 Поняття похідної
Поняття похідної
Постановка задачі. За означенням, знайти похідну функції в точці .
План розв’язання.
1. За означенням
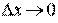
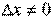
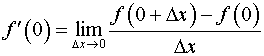 .
.
Зауваження. При обчисленні границі , але .
2. Обчислюємо границю
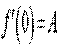
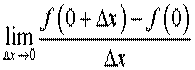 .
.
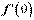 3. Якщо границя існує і дорівнює А, то , якщо границя не існує, то не існує.
3. Якщо границя існує і дорівнює А, то , якщо границя не існує, то не існує.
Задача 1. Виходячи з означення похідної, знайти 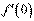 .
.
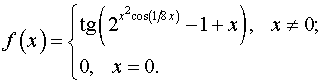
Виходячи з означення похідної, маємо:
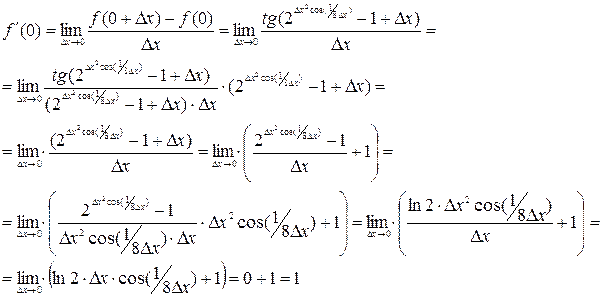
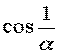 | |||
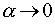 | |||
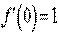 Так як хоча при не визначений, але є скінченою. величиною.
Так як хоча при не визначений, але є скінченою. величиною.
Тобто задана функція в точці х = 0 має похідну, яка дорівнює одиниці: .
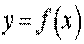 Рівняння дотичної і нормаліПостановка задачі.
Рівняння дотичної і нормаліПостановка задачі.
Скласти рівняння дотичної і/або нормалі до кривої в точці з абсцисою х0.
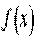 План розв’язання.Якщо функція в точці х0 має кінцеву похідну, то рівняння дотичної має вигляд
План розв’язання.Якщо функція в точці х0 має кінцеву похідну, то рівняння дотичної має вигляд
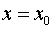
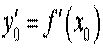
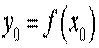
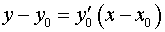 , (1)
, (1)
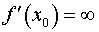 де і .
де і .
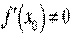 Якщо , то рівняння дотичної має вигляд х = х0.
Якщо , то рівняння дотичної має вигляд х = х0.
Якщо , то рівняння нормалі має вигляд
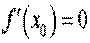
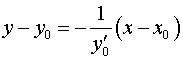 . (2)
. (2)
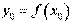 Якщо , то рівняння нормалі має вигляд х = х0.
Якщо , то рівняння нормалі має вигляд х = х0.
1. Знаходимо значення .
2. Знаходимо похідну 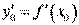 .
.
3. Підставляючи знайдені значення У0 й У0' у (1) і/або (2), одержуємо рівняння дотичної і/або нормалі.
Задача 2. Скласти рівняння нормалі до даної кривої в точці з абсцисою х0.
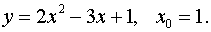
Рівняння нормалі:
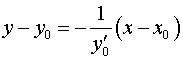 .
.
Маємо:
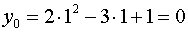 .
.
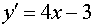 ,
, 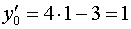 .
.
Одержуємо рівняння нормалі:
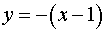 або
або 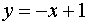 .
.
Скласти рівняння дотичної до даної кривої в точці з абсцисою х0.
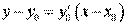
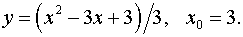
Рівняння дотичної: .
Маємо:
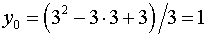 .
.
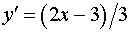 ,
, 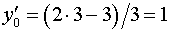 .
.
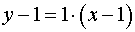 Одержуємо рівняння дотичної:
Одержуємо рівняння дотичної:
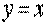 або
або
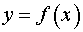 Диференціал
Диференціал
Постановка задачі. Знайти диференціал dy функції .
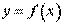 План розв’язання
План розв’язання
Диференціалом функції в точці х називається головна частина її збільшення, рівна добуткові похідної функції на приріст аргументу, і позначається dy (або 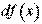 ):
):
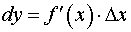 . (1)
. (1)
Диференціал dy називають також диференціалом першого порядку. Тому що для функції у = х маємо у' = х' = 1, тобто відповідно до формули (1), маємо dy = dx = ∆x, тобто диференціал незалежної змінної дорівнює збільшенню цієї змінної: dx = ∆x.
Тому формулу (1) можна записати так:
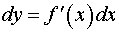 , (2)
, (2)
іншими словами, диференціал функції дорівнює добуткові похідної цієї функції на диференціал незалежної змінної.
Задача 3. Знайти диференціал dy.
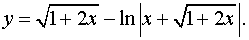
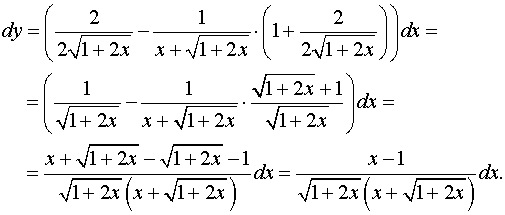
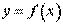 Наближені обчислення за допомогою диференціала
Наближені обчислення за допомогою диференціала
Постановка задачі. Обчислити приблизно за допомогою диференціала значення функції
в точці x0.
План розв’язання. Якщо приріст ∆x = x – x0 аргументу x мал за абсолютною величиніою, то
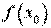
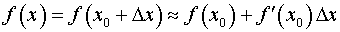 . (1)
. (1)
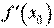
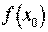 1. Вибираємо точку x0, найближчу до x і таку, щоб легко обчислювалися значення і
1. Вибираємо точку x0, найближчу до x і таку, щоб легко обчислювалися значення і 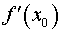 .
.
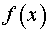 2. Обчислюємо ∆x = x – x0 , і .
2. Обчислюємо ∆x = x – x0 , і .
3. По формулі (1) обчислюємо .
Задача 4. Обчислити приблизно за допомогою диференціала.
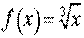
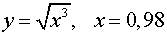 .
.
У нашому випадку: x0 = 1, , ∆x = 0,98 – 1 = – 0,02.
Обчислюємо:
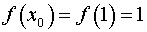 ;
;
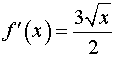 ,
, 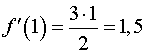 .
.
Маємо:
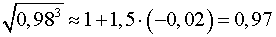
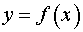 Обчислення похідних
Обчислення похідних
Постановка задачі. Знайти похідну функції .
План розв’язання. Задача розв’ язуеться в кілька етапів. На кожному етапі необхідно розпізнати тип функції і застосувати відповідне правило диференціювання. Можливі наступні типи функцій.
1. Функція має вигляд С1u1(x) + С2u2 (x) + … + Сnun(x), де u1(x), u2(x), …, un(x) – деякі функції і C1,С2, …, Сn – деякі постійні (константи). Використовуємо формулу похідної лінійної комбінації
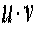
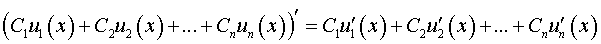 .
.
2. Функція має вигляд . Використовуємо формулу похідної добутку:
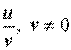
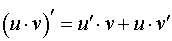 .
.
3. Функція має вигляд . Використовуємо формулу похідної частки:
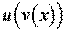
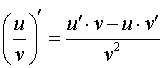 .
.
4. Функція має вигляд . Використовуємо формулу похідної складної функції:
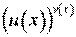
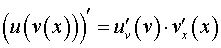 .
.
5. Функція має вигляд . Похідна такої функції обчислюється за допомогою формули
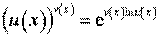 .
.
Перехід від етапу до етапу відбувається доти, поки під кожним знаком похідної не виявиться таблична функція.
Таблиця похідних основних елементарних функцій.
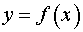 Функція Функція | 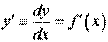 Похідна Похідна |
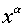 | 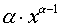 |
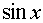 | 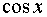 |
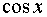 | 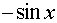 |
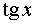 | 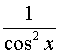 |
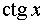 | 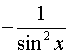 |
 | 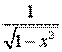 |
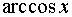 | 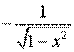 |
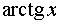 | 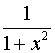 |
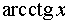 | 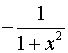 |
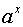 | 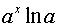 |
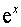 | 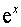 |
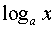 | 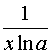 |
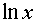 | 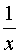 |
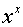 | 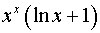 |
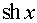 | 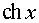 |
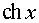 | 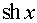 |
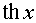 | 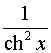 |
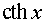 | 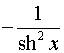 |
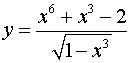 Задача 5.Знайти похідну.
Задача 5.Знайти похідну.
.
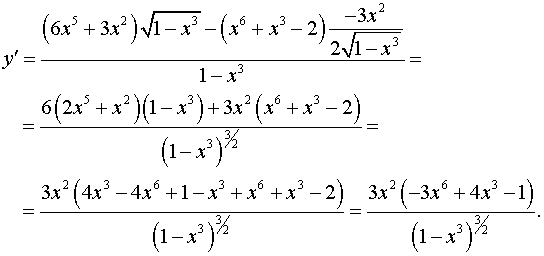
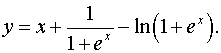 Задача 6.Знайти похідну.
Задача 6.Знайти похідну.
.
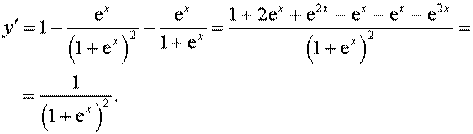
Задача 7.Знайти похідну.
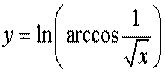 .
.
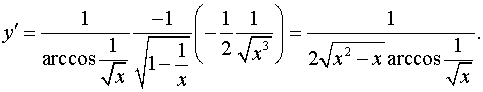
Задача 8.Знайти похідну.
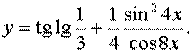 .
.
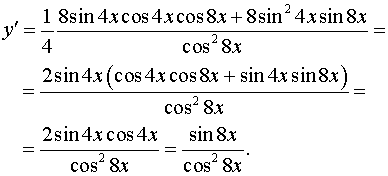
Задача 9.Знайти похідну.
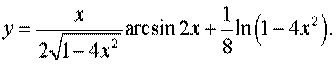 .
.
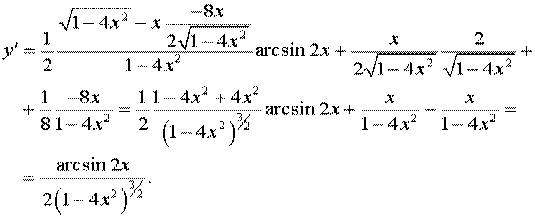
Задача 10.Знайти похідну.
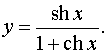 .
.