Найти соответствие между функцией и её производной

Урок по теме «Производная в технике, физике, химии, экономике. . .»

С использованием компьютерных технологий

«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И. Лобачевский

Скажи мне, и я забуду. Покажи мне, и я запомню. Дай мне действовать самому, И я научусь Конфуций

ЦЕЛИ УРОКА:

- добиться усвоения учащимися систематических, осознанных сведений о понятии производной, её геометрическом и физическом смысле;

- формировать навыки практического использования производной в предметах школьного курса, показать применение производной при решении жизненно важных задач;

- развивать познавательный интерес у учащихся через раскрытие практической необходимости и теоретический значимости темы и использование возможностей ЭВМ в изучении темы;

- формировать у учащихся понятие о научной организации труда с помощью ЭВМ;

ОБОРУДОВАНИЕ: компьютерный класс.

ПЛАН УРОКА

I. ОРГАНИЗАЦИОННЫЙ ЭТАП.

Показатели выполнения психологической задачи этапа:

• доброжелательный настрой учителя и учащихся;
• быстрое включение класса в деловой ритм;
• организация внимания всех учащихся;
• кратковременность организационного момента;
• полная готовность класса и оборудования к работе.

Ролевая игра: дежурный системный администратор.
На данном этапе важно, чтобы учащиеся не «отнимали» время урока на ввод пароля и логина, не ждали загрузки учебного сайта или не инсталлировали программы, а занимались именно предметом, но на компьютере. И в этом учителю может помочь дежурный системный администратор, который выбирается из числа учеников, которые достаточно хорошо разбираются в компьютерных хитростях. Именно он и подготавливает компьютерный класс к уроку: загружает, инсталлирует, устанавливает…

II.ЭТАП ПРОВЕРКИ ДОМАШНЕГО ЗАДАНИЯ

Показатели выполнения учебно-воспитательной задачи этапа:

• выявление факта выполнения домашнего задания у всего класса за короткий промежуток времени (5-7 мин.), устранение типичных ошибок;
• обнаружение причин невыполнения домашнего задания отдельными учащимися;
• формирование понимания у учащихся связи выполнения домашней работы с результатами своего обучения вообще;
• использование различных форм контроля в зависимости от вида и цели домашнего задания, от отношения учеников данного класса к выполнению домашней работы

На данном этапе предлагается следующее:

1. Электронное домашнее задание. Его не обязательно выполнять дома (не у всех есть домашние компьютеры) – можно использовать мощности школьного компьютерного класса. Сохранение электронных домашних работ занимает мало времени. Одновременно учителем могут быть предложены некоторые дополнительные «критерии для сохранения выполненного домашнего задания»: самооценка (папки «Отлично», «Хорошо», «Удовлетворительно»), интерес («интересно», «неинтересно») и т.п. своей работы каждым учеником. Создав заранее в именной папке учителя систему дополнительных папок, можно получить интересные результаты на этапе сдачи домашней работы в электронном виде.
2. Создание «разминочных тестов» - без автоматической отметки - с помощью панели инструментов «Формы» в MS Word и в программе PowerPoint.

III. ЭТАП АКТУАЛИЗАЦИИ ОПОРНЫХ ЗНАНИЙ УЧАЩИХСЯ

Показатели выполнения учебно-воспитательной задачи этапа:

• проверка учителем не только объема и правильности знаний, но также их глубины, осознанности, гибкости и оперативности, умения использовать их на практике;
• рецензирование ответов, направленное на указание положительных и отрицательных сторон в знаниях;
• активная деятельность всего класса в ходе проверки знаний отдельных учащихся.

На данном этапе предлагается следующее:

1. Электронный кроссворд " Мысли в фокус"

1. Угол ее наклона выражает геометрический смысл производной.

2. Великий немецкий ученый, философ, математик, физик, юрист, языковед,

создатель математического анализа, основоположник большой математической школы.

3. Раздел физики, помогающий понять смысл производной.

4. Точка интриганка, точка … .

5."Microsoft Windows в переводе на русский "Компания …"

6. Имя английского физика и математика, автора сочинения "Математические начала натуральной философии"

7. Маленькая, серенькая на коврике лежит. Что это?

8. Утверждение, которое в ходе исследовательской работы подтверждается или опровергается.

9. Синоним понятию "дифференциальное исчисление"

10. Производная- это….

11. Внешний носитель информации в компьютере.

12. Устройство вывода информации в компьютере.

13. Одна из эффективных форм проверки знаний учащихся.

14. "Любите … - источник знаний".

15. Соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число y, зависящее от х.

2. У с т н ы й б л и ц – о п р о с

Учитель информатики:

1. Какая программа используется для организации работы кроссворда?

2. Какие функции и логические выражения используются для работы кроссворда ?

Учитель математики:

а) Что называется производной функции в точке?

Ответ: производной функции у = f(x) в точке х₀ называется предел отношения

приращения функции в точке х₀ к приращению аргумента, когда последнее стремится к нулю.

б) В чем заключается геометрический смысл производной?

Ответ: значение производной f '(x) при данном значении аргумента x равно тангенсу угла,

образованного с положительным направлением оси Ox касательной к графику функции f(x) в

точке M(x, f(x)). k = tga = f '(x₀).

в) В чем заключается механический смысл производной?

Ответ: произ­водная функции y = f(x) в точке x₀ - это скорость изменения функции f (х) в

точке x₀ x'(t). = n(t)

5) На рисунках изображены графики функций и касательные к ним в точке а. Укажите функцию, производная которой в точке а равна 1.

Ответ: (3)

1)		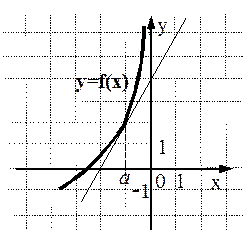2)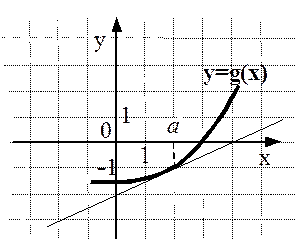
3)		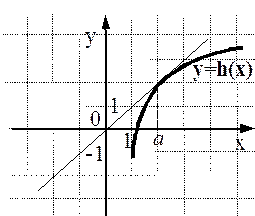4)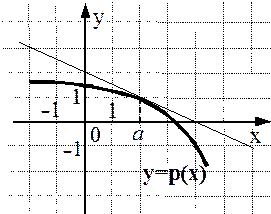

Интерактивный тест

Учитель математики:

Найти соответствие между функцией и её производной.

Учитель информатики: