Примеры решения систем линейных алгебраических уравнений матричным методом
Матричный метод решения систем линейных алгебраических уравнений - вывод формулы.
Пусть для матрицы А порядка n на n существует обратная матрица 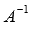 . Умножим обе части матричного уравнения
. Умножим обе части матричного уравнения 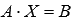 слева на
слева на 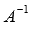 (порядки матриц A ⋅ X и Впозволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем
(порядки матриц A ⋅ X и Впозволяют произвести такую операцию, смотрите статью операции над матрицами, свойства операций). Имеем 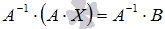 . Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как
. Так как для операции умножения матриц подходящих порядков характерно свойство ассоциативности, то последнее равенство можно переписать как 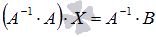 , а по определению обратной матрицы
, а по определению обратной матрицы 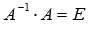 (E – единичная матрица порядка n на n), поэтому
(E – единичная матрица порядка n на n), поэтому
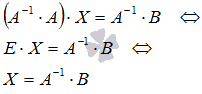
Таким образом, решение системы линейных алгебраических уравнений матричным методом определяется по формуле 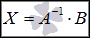 . Другими словами, решение СЛАУ находится с помощью обратной матрицы
. Другими словами, решение СЛАУ находится с помощью обратной матрицы 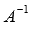 .
.
Мы знаем, что квадратная матрица А порядка n на n имеет обратную матрицу 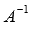 только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ nЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
только тогда, когда ее определитель не равен нулю. Следовательно, СИСТЕМУ nЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ НУЛЯ.
К началу страницы
Примеры решения систем линейных алгебраических уравнений матричным методом.
Рассмотрим матричный метод на примерах. В некоторых примерах мы не будем подробно описывать процесс вычисления определителей матриц, при необходимости обращайтесь к статье вычисление определителя матрицы.
Пример.
С помощью обратной матрицы найдите решение системы линейных уравнений 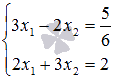 .
.
Решение.
В матричной форме исходная система запишется как 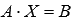 , где
, где 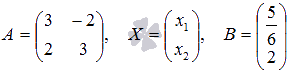 . Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем
. Вычислим определитель основной матрицы и убедимся, что он отличен от нуля. В противном случае мы не сможем решить систему матричным методом. Имеем 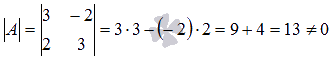 , следовательно, для матрицы А может быть найдена обратная матрица
, следовательно, для матрицы А может быть найдена обратная матрица 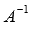 . Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как
. Таким образом, если мы отыщем обратную матрицу, то искомое решение СЛАУ определим как 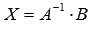 . Итак, задача свелась к построению обратной матрицы
. Итак, задача свелась к построению обратной матрицы 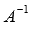 . Найдем ее.
. Найдем ее.
Мы знаем, что для матрицы 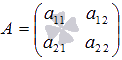 обратная матрица может быть найдена как
обратная матрица может быть найдена как 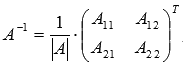 , где
, где 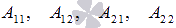 - алгебраические дополнения элементов
- алгебраические дополнения элементов 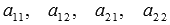 .
.
В нашем случае
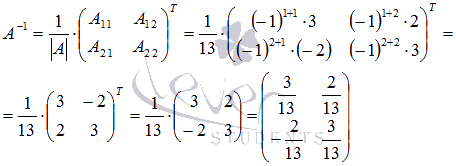
Тогда
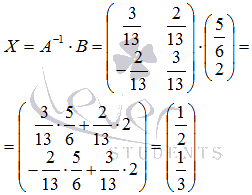
Выполним проверку полученного решения 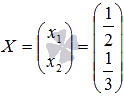 , подставив его в матричную форму исходной системы уравнений
, подставив его в матричную форму исходной системы уравнений 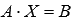 . Это равенство должно обратиться в тождество, в противном случае где-то была допущена ошибка.
. Это равенство должно обратиться в тождество, в противном случае где-то была допущена ошибка.
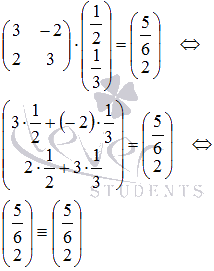
Следовательно, решение найдено верно.
Ответ:
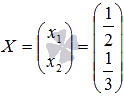 или в другой записи
или в другой записи 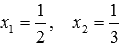 .
.
Пример.
Решите СЛАУ 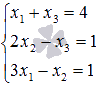 матричным методом.
матричным методом.
Решение.
Первое уравнение системы не содержит неизвестной переменной x2, второе –x1, третье – x3. То есть, коэффициенты перед этими неизвестными переменными равны нулю. Перепишем систему уравнений как 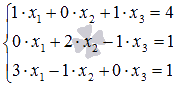 . От такого вида проще перейти к матричной форме записи СЛАУ
. От такого вида проще перейти к матричной форме записи СЛАУ 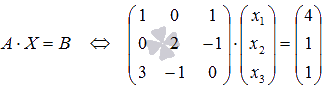 . Убедимся в том, что эта система уравнений может быть решена с помощью обратной матрицы. Другими словами, покажем что
. Убедимся в том, что эта система уравнений может быть решена с помощью обратной матрицы. Другими словами, покажем что 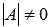 :
:
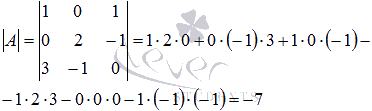
Построим обратную матрицу 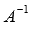 с помощью матрицы из алгебраических дополнений:
с помощью матрицы из алгебраических дополнений:
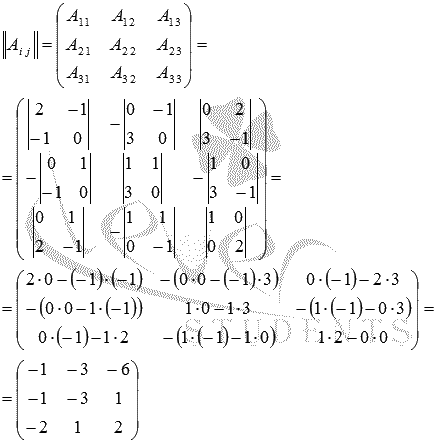
тогда,
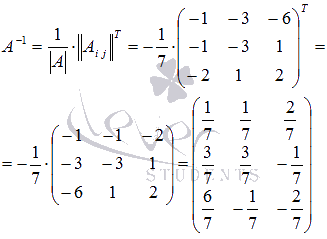
Осталось найти решение СЛАУ:
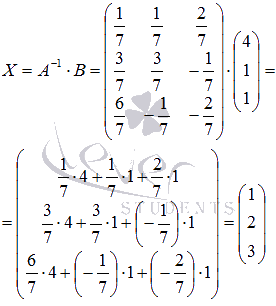
Рекомендуем выполнить проверку.
Ответ:
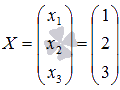 .
.
При переходе от обычного вида системы линейных алгебраических уравнений к ее матричной форме следует быть внимательным с порядком следования неизвестных переменных в уравнениях системы. К примеру, СЛАУ 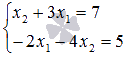 НЕЛЬЗЯ записать как
НЕЛЬЗЯ записать как 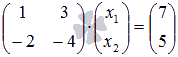 . Нужно сначала упорядочить все неизвестные переменные во всех уравнениях системы, а потом переходить к матричной записи:
. Нужно сначала упорядочить все неизвестные переменные во всех уравнениях системы, а потом переходить к матричной записи:
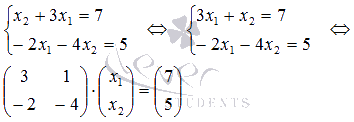
или
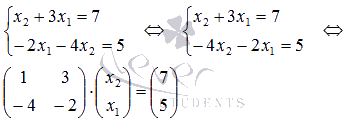
Также будьте внимательны с обозначением неизвестных переменных, вместоx1, x2, …, xn могут быть любые другие буквы. Например, СЛАУ 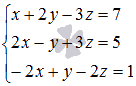 в матричной форме запишется как
в матричной форме запишется как 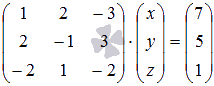 .
.
Разберем пример.
Пример.
Найдите решение системы линейных алгебраических уравнений 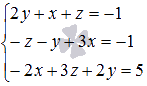 с помощью обратной матрицы.
с помощью обратной матрицы.
Решение.
Упорядочив неизвестные переменные в уравнениях системы, запишем ее в матичной форме 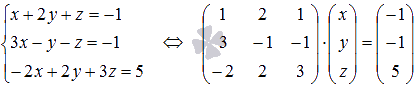 . Вычислим определитель основной матрицы:
. Вычислим определитель основной матрицы:
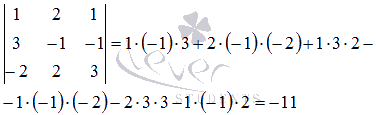
Он отличен от нуля, поэтому решение системы уравнений может быть найдено с помощью обратной матрицы как 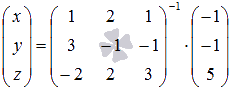 . Найдем обратную матрицу по формуле
. Найдем обратную матрицу по формуле 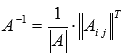 :
:
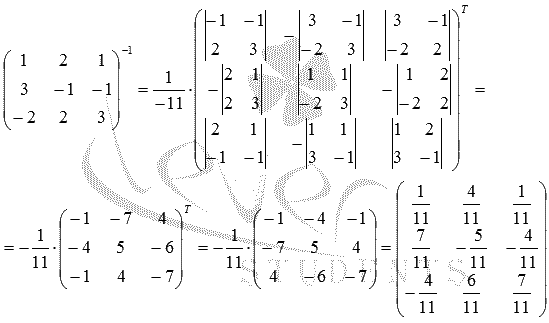
Получим искомое решение:

Ответ:
x = 0, y = -2, z = 3.
Пример.
Найдите решение системы линейных алгебраических уравнений 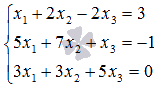 матричным методом.
матричным методом.
Решение.
Определитель основной матрицы системы равен нулю
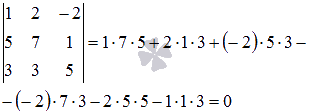
поэтому, мы не можем применить матричный метод.
Нахождение решения подобных систем описано в разделе решение систем линейных алгебраических уравнений.
Пример.
Решите СЛАУ 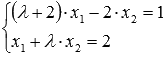 матричным методом,
матричным методом, 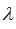 - некоторое действительное число.
- некоторое действительное число.
Решение.
Система уравнений в матричной форме имеет вид 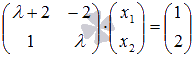 . Вычислим определитель основной матрицы системы и убедимся в том, что он отличен от нуля:
. Вычислим определитель основной матрицы системы и убедимся в том, что он отличен от нуля:
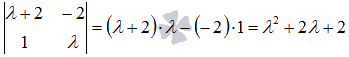
Квадратных трехчлен 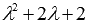 не обращается в ноль ни при каких действительных значениях
не обращается в ноль ни при каких действительных значениях 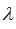 , так как его дискриминант отрицателен
, так как его дискриминант отрицателен 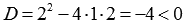 , поэтому определитель основной матрицы системы не равен нулю ни при каких действительных
, поэтому определитель основной матрицы системы не равен нулю ни при каких действительных 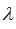 . По матричному методу имеем
. По матричному методу имеем 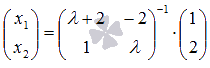 . Построим обратную матрицу по формуле
. Построим обратную матрицу по формуле 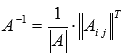 :
:
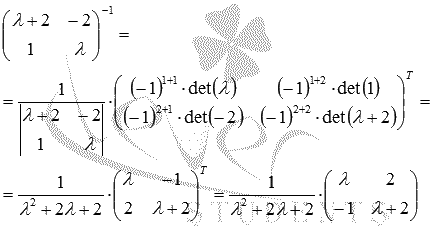
Тогда
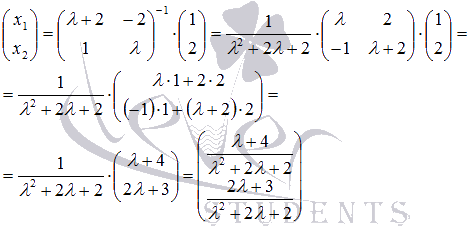
Рекомендуем выполнить проверку полученного результата.
Ответ:
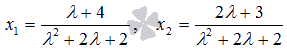 .К началу страницы
.К началу страницы
Подведем итог.
Матричный метод подходит для решения СЛАУ, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы отличен от нуля. Если система содержит больше трех уравнений, то нахождение обратной матрицы требует значительных вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.
