Отношение. Проценты. Пропорции
Отношением числа x к числу y называется частное чисел x и y, то есть 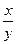 или х : у. Отношение
или х : у. Отношение 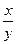 означает во сколько раз x больше y, или какую часть числа y составляет число x.
означает во сколько раз x больше y, или какую часть числа y составляет число x.
Пропорцией называется равенство двух отношений, то есть 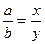 .
.
а и y называются крайними членами, x и b называются средними членами пропорции.
Свойства пропорции.
· произведение крайних членов пропорции равно произведению её средних членов, то есть если 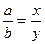 , то
, то 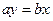 .
.
· обратно: числа a,b,x,y составляют пропорцию 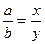 , если
, если 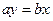 .
.
· из пропорции 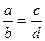 вытекают пропорции
вытекают пропорции 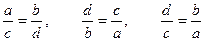 , то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
, то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
· чтобы найти неизвестный средний (крайний) член пропорции, надо произведение крайних (средних) членов разделить на известный средний (крайний) член пропорции
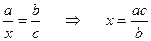 ;
;
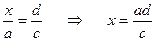 .
. 
Процентом называется сотая часть какого-либо числа. Процент обозначается знаком % .
Чтобы число процентов выразить в виде дроби, достаточно число процентов разделить на сто.
Например: 125%=1,25; 2,3%=0,023.
Нахождение процентов данного числа. Чтобы найти а% от числа b, надо b умножить на а и разделить на 100.
Например: 30% от 60 составляют 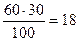 .
.
Нахождение числа по его процентам. Чтобы найти процентное отношение двух чисел a и b, надо отношение чисел умножить на 100%, то есть 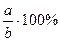 .
.
Например: при плановом задании 60 автомобилей в день завод выпускает 66 автомобилей. На сколько процентов выполнен план?
Решение: 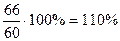 .
.
Целые числа
Два числа, отличающиеся друг от друга только знаком, называются противоположными числами: 1 и -1, 2 и -2, 15 и -15,…
Числа натуральные, им противоположные, а так же число нуль составляют множество целых чисел Z.
Множество натуральных чисел, дополненное нулем, называется множеством целых неотрицательных чисел.
Для целых чисел определены действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, причем сложение, вычитание и умножение выполняются всегда.
Рациональные числа
Объединение множеств целых и дробных чисел (положительных и отрицательных) составляет множество рациональных чисел Q. Любое рациональное число 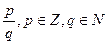 может быть представлено в виде конечной или бесконечной периодической десятичной дроби.
может быть представлено в виде конечной или бесконечной периодической десятичной дроби.
На множестве рациональных чисел можно производить действия сложения, вычитания, умножения, деления (кроме деления на нуль).
Иррациональные числа
Иррациональным числом называют бесконечную десятичную непериодическую дробь. Множество таких дробей составляет множество иррациональных чисел I.
Например: 0,131331333125…;
π ≈ 3,14;
e ≈ 2,7;
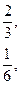 и т.д.
и т.д.
Действительные числа
Объединение множества рациональных чисел и множества иррациональных чисел даёт множество действительных чисел, которое обозначается R.
