Понятие логарифма и его свойства
Логарифмом числа b (b>0) по основанию а(а>0 а¹1)называют показатель степени, в которую нужно возвести число а, чтобы получить число b:
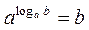 (1)
(1)
Формулу (1) называют основным логарифмическим тождеством.
Логарифм числа b по основанию 10 называется десятичным логарифмом и обозначается 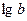 .
.
Логарифм по основанию e (e = 2,71828…) называется натуральным логарифмом и обозначается 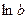 .
.
Свойства логарифмов:
Пусть 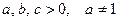 . Тогда:
. Тогда:
1) 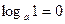 ;
;
2) 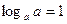 ;
;
3) 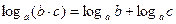 ;
;
4) 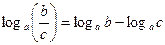 ;
;
5) 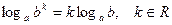 ;
;
6) 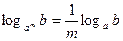 ,
, 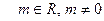 ;
;
7) 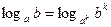 ,
, 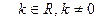 ;
;
8) 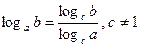 ;
;
9) 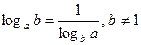 ;
;
10) 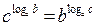 ;
;
11) 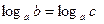 тогда и только тогда, когда
тогда и только тогда, когда 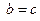 ;
;
12) 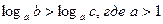 , тогда и только тогда, когда
, тогда и только тогда, когда 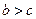 ;
;
13) 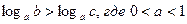 , тогда и только тогда, когда
, тогда и только тогда, когда 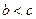 .
.
Обобщенные свойства логарифмов
Пусть 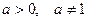 и
и 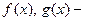 выражения с переменной. Тогда:
выражения с переменной. Тогда:
3*) 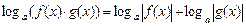 , где
, где 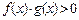 ;
;
4*) 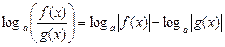 , где
, где  ;
;
5*) 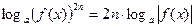 , где
, где 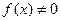 ;
;
6*) 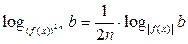 , где
, где 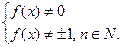
Замечание 1. Следует различать произведение логарифмов 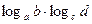 и повторный логарифм
и повторный логарифм 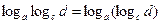 ,
, 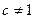 .
.
Замечание 2. Степень логарифма может быть записана двумя способами:
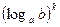 или
или 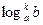 .
.
Логарифмированием называется операция нахождения логарифма числа или выражения.
Потенцированием называют действие, обратное логарифмированию, т.е. потенцирование – это операция нахождения числа (выражения) по его логарифму. При выполнении этих операций пользуются свойствами логарифмов.
Пример 1. Упростить выражение: 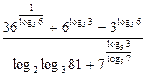 .
.
Решение. Преобразуем каждое слагаемое отдельно. При этом сделаем ссылку на конкретные свойства логарифмов, приведенные выше.
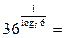 |используем свойство 9|
|используем свойство 9| 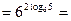 |по свойству 5|=
|по свойству 5|= 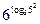 = |по основному логарифмическому тождеству| =
= |по основному логарифмическому тождеству| = 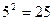 .
.
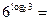 |по свойству 10|
|по свойству 10| 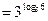 ,
,
тогда 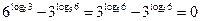 .
.
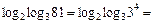 |по свойству 5| =
|по свойству 5| = 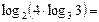
= |по свойству 2| = 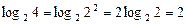 .
.
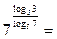 |по свойству 8| =
|по свойству 8| = 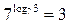 .
.
Таким образом:
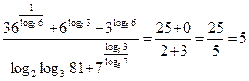 .
.
Замечание 1. Решение этого примера при одновременном преобразовании всех слагаемых (что и следует делать) выглядит так:
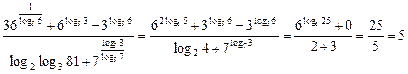
Ответ: 5.
Пример 2. Вычислить: 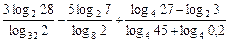 .
.
Решение.Для преобразования первого и второго слагаемых используем формулу изменения основания логарифма (свойство 9), а затем свойства 3 и 5.
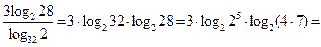
= |по свойствам 5 и 2|=
= 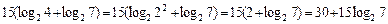
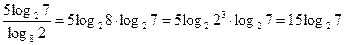 .
.
Для преобразования третьего слагаемого используем свойства 3 – 5:
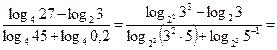
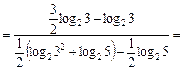
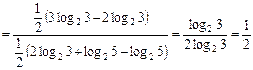
Тогда получаем
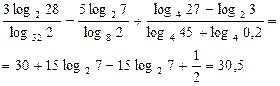 .
.
Ответ: 30,5.
Замечание 2. Подробное описание решения и преобразование всех слагаемых отдельно сделано из соображений доступности объяснений. Целесообразно делать преобразования всего выражения сразу, аналогично тому, как сделано в замечании 1.
Пример 3.Прологарифмировать по основанию 10 выражение
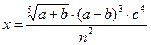 .
.
Решение.Замечаем, что сделать это можно, если 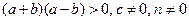 . Тогда
. Тогда
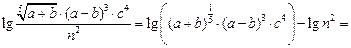
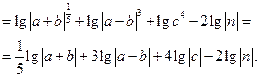
Пример 4. Выполнить потенцирование выражения
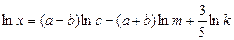 .
.
Решение. Используем свойства логарифмов 3 – 5 («справа-налево»)
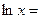
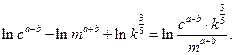
Получаем ответ: 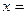
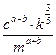 .
.
Пример 5. Выразить 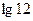 через
через 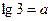 и
и 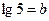 .
.
Решение. 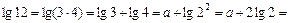
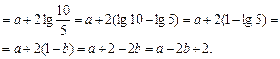
Ответ: 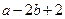 .
.
Задания
I уровень
1.1. Найдите число, логарифм которого при основании 2 равен:
1) 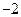 ; 2)
; 2) 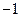 ; 3)
; 3) 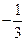 ; 4)
; 4) 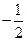 ;
;
5) 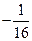 ; 5)
; 5) 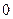 ; 6)
; 6) 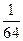 ; 7)
; 7) 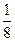 ;
;
8) 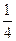 ; 8)
; 8) 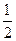 ; 9) 1; 10) 2.
; 9) 1; 10) 2.
1.2. Найдите логарифм числа 729 при основании
1) 9; 2) 3; 3) 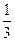 ; 4)
; 4) 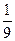 .
.
1.3. Найдите логарифм по основанию 3 числа:
1) 1; 2) 3; 3) 9; 4) 27;
5) 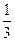 ; 6)
; 6) 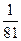 ; 7)
; 7) 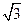 ; 8)
; 8) 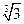 ;
;
9) 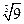 ; 10)
; 10) 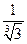 ; 11)
; 11) 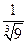 ; 12)
; 12) 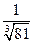 .
.
1.4. Найдите число 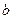 , если:
, если:
1) 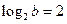 ; 2)
; 2) 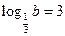 ; 3)
; 3) 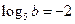 ;
;
4) 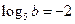 ; 5)
; 5) 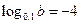 ; 6)
; 6) 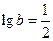 ;
;
7) 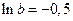 ; 8)
; 8) 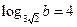 ; 9)
; 9) 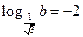 .
.
1.5. Найдите число 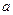 , если
, если
1) 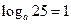 ; 2)
; 2) 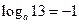 ; 3)
; 3) 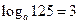 ;
;
4) 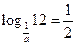 ; 5)
; 5) 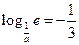 6)
6) 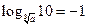 .
.
1.6. Вычислите значение логарифма:
1) 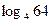 ; 2)
; 2) 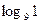 ; 3)
; 3) 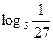 ;
;
4) 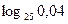 ; 5)
; 5) 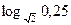 ; 6)
; 6) 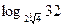 ;
;
7) 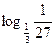 ; 8)
; 8) 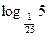 ; 9)
; 9) 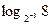 ;
;
10) 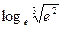 ; 11)
; 11) 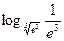 ; 12)
; 12) 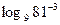 .
.
1.7. Упростите выражение:
1) 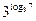 ; 2)
; 2) 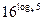 ; 3)
; 3) 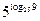 ; 4)
; 4) 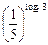 ;
;
5) 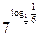 ; 6)
; 6) 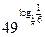 ; 7)
; 7) 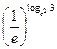 ; 8)
; 8) 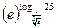 .
.
1.8. Вычислите:
1) 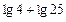 ; 2)
; 2) 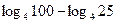 ;
;
3) 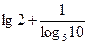 ; 4)
; 4) 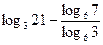 ;
;
5) 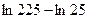 .
.
1.9. Прологарифмируйте выражение по основанию a:
1) 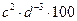 , если
, если 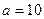 ;
;
2) 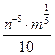 , если
, если 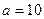 ;
;
3) 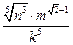 , если a = 10;
, если a = 10;
4) 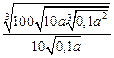 , если a = 10;
, если a = 10;
5) 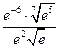 , если
, если 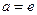 ;
;
6) 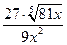 , если
, если 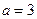 ;
;
7) 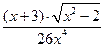 , если
, если 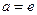 .
.
1.10. Выполните потенцирование:
1) 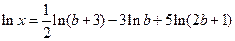 ;
;
2) 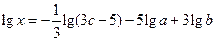 ;
;
3) 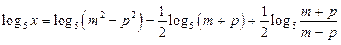 ;
;
II уровень
2.1. Вычислите:
1) 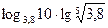 ; 2)
; 2) 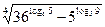 ;
;
3) 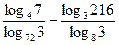 ; 4)
; 4) 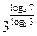 ;
;
5) 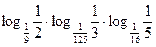 ; 6)
; 6) 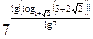 ;
;
7) 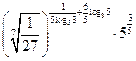 ;
;
8) 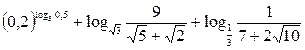 ;
;
9) 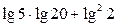 ; 10)
; 10) 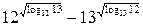 ;
;
11) 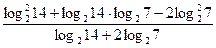 ;
;
12) 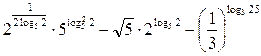 ;
;
13) 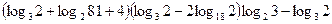 ;
;
14) 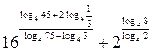 ;
;
15) 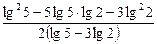 ;
;
16). 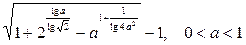 .
.
2.2. Докажите неравенство:
1). 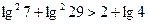 ; 2).
; 2). 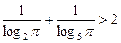 .
.
2.3. Известно, что 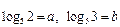 . Выразите заданный логарифм через a и b:
. Выразите заданный логарифм через a и b:
1) 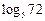 ; 2)
; 2) 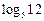 ; 3)
; 3) 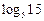 ; 4)
; 4) 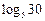 .
.
III уровень
3.1.Вычислите:
1). 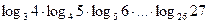 ;
;
2). 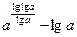 ;
;
3). 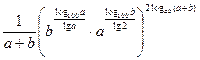 ;
;
4). 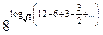 .
.
3.2. Упростите до числа:
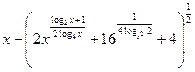 .
.
3.3. Докажите, что
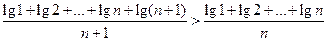 .
.
