Свойства обратной матрицы
1.Обратная матрица единственна.
Доказательство.Пусть существуют две обратные матрицы: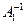 
и 
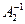. Тогда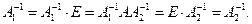 
2. 
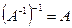. Это следует из определения.
3. 
.
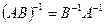Доказательство: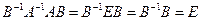 
и
.
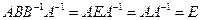4. 
.
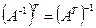Доказательство: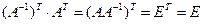 
и
.
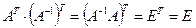5.Если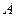 
– невырожденная матрица, то 
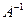– тоже невырожденная.
Доказательство: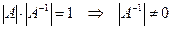 
.
Пример.Найти обратную матрицу для матрицы
.
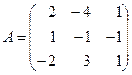Найдём определитель матрицы :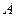
,
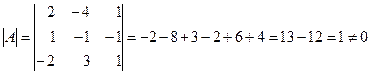следовательно, существует обратная матрица.
Вычислим алгебраические дополнения всех элементов матрицы 
:
; 
; 
; 
; 
; 
;
; 
; 
,
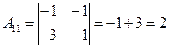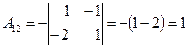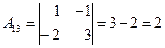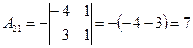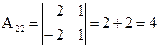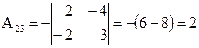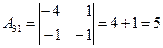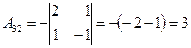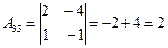тогда
.
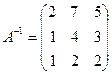Проверка
.
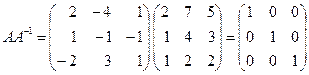Лекция 5
Понятие линейной зависимости строк матрицы, основные теоремы.
Элементарные преобразования матриц. Ступенчатые матрицы. Приведение матрицы к ступенчатому и единичному виду. Построение обратной матрицы с помощью элементарных преобразований.
Понятие линейной зависимости строк матрицы, основные теоремы
Основная литература: [1], [4].
Элементарные преобразования матриц. Ступенчатые матрицы.
Приведение матрицы к ступенчатому и единичному виду.
Построение обратной матрицы с помощью элементарных преобразований
Определение. Элементарными преобразованиями матрицы называют следующие действия:
1) транспонирование матрицы;
2) умножение всех элементов строки (столбца) матрицы на число, отличное от нуля;
3) изменение порядка строк (столбцов) матрицы;
4) прибавление к каждому элементу строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
5) отбрасывание нулевой строки (столбца).
Алгоритм приведения матрицы к ступенчатому виду
1) Из всех строк матрицы выбрать такую строку, первый элемент которой равен единице. Если такой строки нет, то получить ее с помощью элементарного преобразования 4. Меняя порядок строк, сделать выбранную строку первой строкой.
2) С помощью элементарного преобразования 4 получить нули во всех строках первого столбца, кроме первой.
3) Из всех строк матрицы, кроме первой, выбрать такую строку, второй элемент которой равен единице. Если такой строки нет, то получить ее с помощью элементарного преобразования 4. Меняя порядок строк, сделать выбранную строку второй строкой.
4) С помощью элементарного преобразования 4 получить нули во всех строках второго столбца, кроме первой и второй.
5) Алгоритм продолжать до тех пор, пока все элементы, лежащие ниже главной диагонали, не обратятся в нуль.
Пример 1.Привести матрицу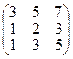 
к ступенчатому виду.
Решение.
.
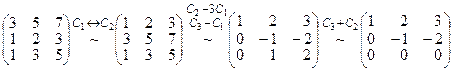Рассмотрим ещё один способ нахождения обратной матрицы с использованием элементарных преобразований.
Пример 2. .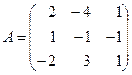
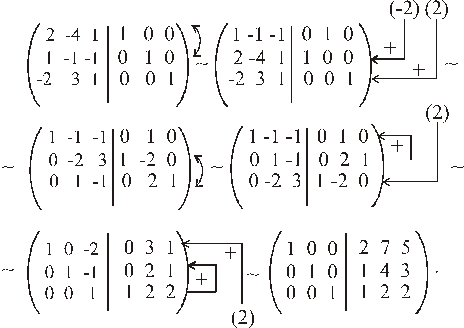
Следовательно, .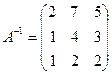
Лекция 6
Ранг матрицы, определение. Понятие базисного минора матрицы.