Как найти длину суммы векторов?
Линейные операции над геометрическими векторами
Произведение вектора на число
Произведением вектора 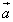 на число
на число 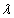 называется вектор, получающийся из вектора
называется вектор, получающийся из вектора 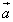 растяжением (при
растяжением (при 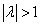 ) или сжатием (при
) или сжатием (при 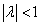 ) в
) в 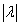 раз, причём направление вектора
раз, причём направление вектора 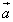 сохраняется, если
сохраняется, если 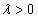 , и меняется на противоположное, если
, и меняется на противоположное, если 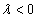 . (Рис. 2)
. (Рис. 2)
Из определения следует, что векторы 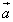 и
и 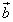 =
= 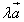 всегда расположены на одной или на параллельных прямых. Такие векторы называютсяколлинеарными. (Можно говорить также, что эти векторы параллельны, однако в векторной алгебре принято говорить "коллинеарны".) Справедливо и обратное утверждение: если векторы
всегда расположены на одной или на параллельных прямых. Такие векторы называютсяколлинеарными. (Можно говорить также, что эти векторы параллельны, однако в векторной алгебре принято говорить "коллинеарны".) Справедливо и обратное утверждение: если векторы 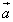 и
и 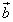 коллинеарны, то они связаны отношением
коллинеарны, то они связаны отношением
 . (1)
. (1)
Следовательно, равенство (1) выражает условие коллинеарности двух векторов.
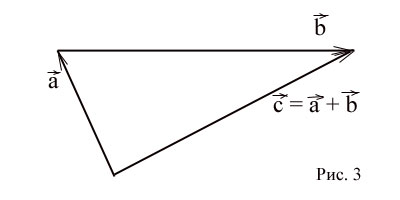
Сумма векторов
Суммой векторов 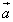 и
и 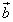 называется вектор
называется вектор  , начало которого совпадает с началом вектора
, начало которого совпадает с началом вектора 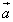 , а конец - с концом вектора
, а конец - с концом вектора 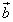 , при условии, что начало вектора
, при условии, что начало вектора 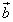 приложено к концу вектора
приложено к концу вектора 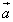 . (Рис. 3)
. (Рис. 3)
Это определение может быть распределено на любое конечное число векторов. Пусть в пространстве даны n свободных векторов  . Если к концу вектора
. Если к концу вектора  приложить начало вектора
приложить начало вектора 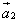 , а к концу вектора
, а к концу вектора 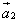 - начало вектора
- начало вектора 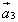 и т.д. и, наконец, к концу вектора
и т.д. и, наконец, к концу вектора 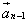 - начало вектора
- начало вектора 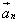 , то суммой этих векторов служит замыкающий вектор
, то суммой этих векторов служит замыкающий вектор 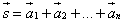 , начало которого совпадает с началом первого вектора
, начало которого совпадает с началом первого вектора 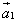 , а конец - с концом последнего вектора
, а конец - с концом последнего вектора 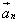 . (Рис. 4)
. (Рис. 4)
Слагаемые 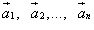 называются составляющими вектора
называются составляющими вектора 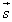 , а сформулированное правило - правилом многоугольника. Этот многоугольник может и не быть плоским.
, а сформулированное правило - правилом многоугольника. Этот многоугольник может и не быть плоским.
При умножении вектора 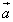 на число -1 получается противоположный вектор
на число -1 получается противоположный вектор 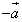 . Векторы
. Векторы 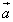 и
и 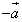 имеют одинаковые длины и противоположные направления. Их сумма
имеют одинаковые длины и противоположные направления. Их сумма 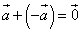 даёт нулевой вектор, длина которого равна нулю. Направление нулевого вектора не определено.
даёт нулевой вектор, длина которого равна нулю. Направление нулевого вектора не определено.
В векторной алгебре нет необходимости рассматривать отдельно операцию вычитания: вычесть из вектора 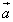 вектор
вектор 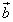 означает прибавить к вектору
означает прибавить к вектору 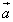 противоположный вектор
противоположный вектор 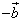 , т.е.
, т.е. 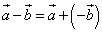
Пример 1. Упростить выражение:
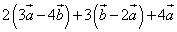 .
.
Решение:
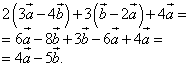 ,
,
то есть, векторы можно складывать и умножать на числа так же, как и многочлены (в частности, также задачи на упрощение выражений). Обычно необходимость упрощать линейно подобные выражения с векторами возникает перед вычислением произведений векторов.
Пример 2. Векторы 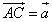 и
и 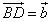 служат диагоналями параллелограмма ABCD (рис. 4а). Выразить через
служат диагоналями параллелограмма ABCD (рис. 4а). Выразить через 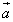 и
и 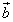 векторы
векторы 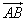 ,
, 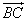 ,
, 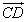 и
и 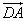 , являющиеся сторонами этого параллелограмма.
, являющиеся сторонами этого параллелограмма.
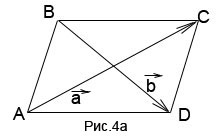
Решение. Точка пересечения диагоналей параллелограмма делит каждую диагональ пополам. Длины искомых векторов находим либо как половины сумм векторов, образующих с искомыми треугольник, либо как половины разностей (в зависимости от направления вектора, служащего диагональю), либо, как в последнем случае, половины суммы, взятой со знаком минус. Итак, искомые векторы равны:
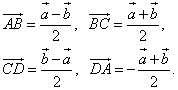
Как найти длину суммы векторов?
Эта задача занимает особое место в операциях с векторами, так как предполагает использование тригонометрических свойств. Допустим, Вам попалась задача вроде следующей:
Даны длины векторов 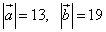 и длина суммы этих векторов
и длина суммы этих векторов 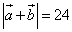 . Найти длину разности этих векторов
. Найти длину разности этих векторов 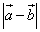 .
.
Решения этой и других подобных задач и объяснения, как их решать - в уроке "Длина суммы векторов и теорема косинусов".
