Сфера, вписанная в многогранник
Определение. Сфера называется вписанной в многогранник, если плоскости всех граней многогранника касаются сферы в тачках, расположенных внутри этих граней. При этом многогранник называется описанным около сферы.
Теорема 1.В произвольный тетраэдр можно вписать сферу (шар).
Множество точек, равноудаленных от боковых граней тетраэдра есть прямая пересечения двух биссекторных плоскостей двугранных углов при двух боковых ребрах. Эту прямую пересечет биссекторная плоскость двугранного угла при основании. Полученная точка равноудалена от всех граней тетраэдра.
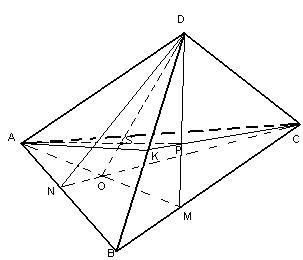
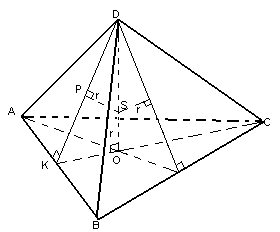
В тетраэдре ABCD плоскости CDN и ADM являются биссекторными плоскостями двугранных углов при боковых ребрах CD и AD. Они пересекаются по прямой OD. Плоскость AKC является бисссекторной плоскостью двугранного угла при основании (ребро AC). Эта плоскость пересечет прямую OD в точке S (P – точка пересечения прямых DM и KC, принадлежащая плоскостям AKC и ADM одновременно, следовательно точка S – точка пересечения AP и OD), которая будет являться точкой, равноудаленной от всех граней тетраэдра и, следовательно, будет являться центром сферы, вписанной в тетраэдр ABCD.
Пример 1. Найти радиус сферы, вписанной в правильный тетраэдр.
Рассмотрим подобные треугольники DPS и DOK (по двум углам: угол D – общий, углы DPS и DOK – прямые).
Тогда PS:KO=DS:DK,
если учесть, что PS=r=SO и DS=DO-SO=DO-r,
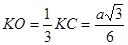 ,
, 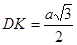 ,
, 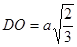 то
то 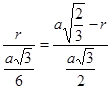
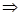
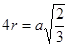
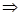
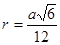 .
.
Ответ: радиус сферы, вписанной в правильный тетраэдр равен 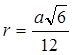
Теорема 2. В правильную пирамиду можно вписать сферу.
Теорема 3. В правильную усеченную пирамиду можно вписать сферу тогда и только тогда, когда ее апофема равна сумме радиусов окружностей, вписанных в ее основания.
Теорема 4. В любую призму можно вписать сферу, если в ее перпендикулярное сечение можно вписать окружность, радиус которой равен половине высоты призмы.
Теорема 5. В правильную призму можно вписать сферу тогда и только тогда, когда высота призмы равна диаметру окружности, вписанной в ее основание.
Сферы, описанные около цилиндра, конуса и
Усеченного конуса.
Определение. Сфера называется описанной около цилиндра или усеченного конуса, если все точки окружностей оснований принадлежат сфере; Сфера называется описанной около конуса, если все точки окружности основания, а также вершина конуса принадлежат сфере.
В этих случаях говорят, что цилиндр, усеченный конус или конус вписан в сферу.
Теорема 1.Около произвольного цилиндра можно описать сферу.
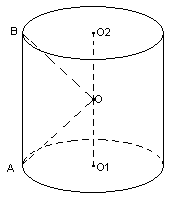
О1 и О2 – центры нижнего и верхнего основания соответственно. Прямая О1О2 перпендикулярна плоскостям основания. Проведем плоскость, проходящую через середину образующей цилиндра, перпендикулярно этой образующей. Эта плоскость будет параллельна плоскостям основания и пересекать прямую О1О2 в точке О, которая и будет являться центром сферы, описанной около цилиндра. Расстояние от точки О до всех точек основания будет равным, так как О1О2 является ГМТ, равноудаленных от окружности (прямая, проходящая через центр окружности и перпендикулярна плоскости окружности). Значит точка О является центром сферы с радиусом ОА, описанной около цилиндра.
Теорема 2. Около усеченного конуса можно описать сферу.
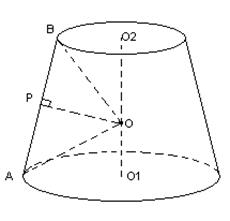
О1 и О2 – центры нижнего и верхнего основания соответственно. Прямая О1О2 перпендикулярна плоскостям основания. Рассмотрим образующую усеченного конуса АВ. Найдем ГМТ, равноудаленных от тачек А и В. Им будет являть плоскость, проходящая через точку Р – середину АВ и перпендикулярная этой прямой. Эта плоскость пересечет О1О2 в точке О, которая будет равноудалена от точек А и В. Также очевидно, что точка О будет равноудалена от все точек оснований усеченного конуса. Следовательно эта точка О будет являться центром сферы с радиусом ОА, описанной около усеченного конуса.
Теорема 3. Около конуса можно описать сферу.
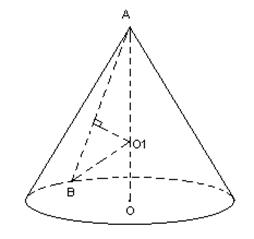
Аналогично прошлой теореме ОА – высота конуса, которая является ГМТ, равноудаленных от окружности. Рассмотрим образующую АВ и найдем ГМТ, равноудаленных от А и В. Полученная плоскость (по предыдущей задаче) пересечет ОА в точке О1, которая будет равноудалена от точек А и В, как и от любых точек основания конуса. Таким образом мы получили, что точка О1 является центром сферы с радиусом О1А, описанной около конуса.
