Момент силы относительно точки и относительно оси

Момент пары сил

Моментом силы относительно какой-либо точки (центра) называется вектор, численно равный произведению модуля силы на плечо, т.е. на кратчайшее расстояние от указанной точки до линии действия силы, и направленный перпендикулярно плоскости, проходящей через выбранную точку и линию действия силы в ту сторону, откуда "вращение", совершаемое силой вокруг точки, представляется происходящим против хода часовой стрелки. Момент силы характеризует ее вращательное действие.

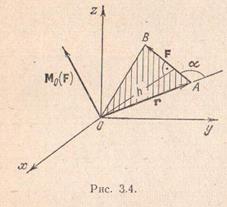Если О – точка, относительно которой находится момент силы F, то момент силы обозначается символом М_о(F). Покажем, что если точка приложения силыFопределяется радиус-вектором r, то справедливо соотношение

М_о(F)=r×F. (3.6)

Согласно этому соотношению момент силы равен векторному произведению вектора r на вектор F.

В самом деле, модуль векторного произведения равен

М_о(F)=rFsin=Fh, (3.7)

где h – плечо силы. Заметим также, что вектор М_о(F) направлен перпендикулярно плоскости, проходящей через векторы rи F, в ту сторону, откуда кратчайший поворот вектора rк направлению вектора Fпредставляется происходящим против хода часовой стрелки. Таким образом, формула (3.6) полностью определяет модуль и направление момента силы F.

Иногда формулу (3.7) полезно записывать в виде

М_о(F)=2S, (3.8)

где S – площадь треугольника ОАВ.

Пусть x, y, z – координаты точки приложения силы, а F_x, F_y, F_z – проекции силы на координатные оси. Тогда, если точка О находится в начале координат, момент силы выражается следующим образом:

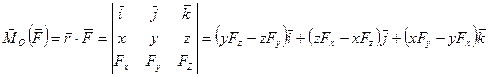. (3.9)

Отсюда следует, что проекции момента силы на координатные оси определяются формулами:

M_Ox(F)= yF_z-zF_y,

M_Oy(F)= zF_x-xF_z,

M_Oy(F)= xF_y-yF_x. (3.10)

Введем теперь понятие проекции силы на плоскость.

Пусть даны сила Fи некоторая плоскость. Опустим из начала и конца вектора силы перпендикуляры на эту плоскость.

Проекцией силы на плоскость называется вектор, начало и конец которого совпадают с проекцией начала и проекцией конца силы на эту плоскость.

Если в качестве рассматриваемой плоскости принять плоскость хОу, то проекцией силы Fна этуплоскость будет вектор F_ху.

Момент силы F_ху относительно точки О (точки пересечения оси z с плоскостью хОу) может быть вычислен по формуле (3.9), если в ней принять z=0, F_z=0. Получим

M_O(F_ху)=(xF_y-yF_x)k.

Таким образом, момент направлен вдоль оси z, а его проекция на ось z в точности совпадает с проекцией на ту же ось момента силы Fотносительно точки О. Другими словами,

M_Oz(F)=M_Oz(F_ху)= xF_y-yF_x. (3.11)

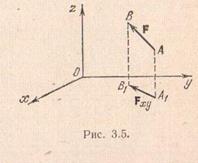Очевидно, тот же результат можно получить, если спроектировать силуFна любую другую плоскость, параллельную хОу. При этом точка пересечения оси z с плоскостью будет уже иной (обозначим новую точку пересечения через О₁). Однако все входящие в правую часть равенства (3.11) величины х, у, F_х, F_уостанутся неизменными, и, следовательно, можно записать

M_Oz(F)=M_O1z(F_ху).

Другими словами, проекция момента силы относительно точки на ось, проходящую через эту точку, не зависит от выбора точки на оси. Поэтому в дальнейшем вместо символа M_Oz(F) будем применять символ M_z(F). Эта проекция момента называется моментом силы относительно оси z. Вычисление момента силы относительно оси часто бывает удобнее производить посредством проектирования силы F на плоскость, перпендикулярную оси, и вычисления величины M _z(F_ху).

В соответствии с формулой (3.7) и учитывая знак проекции, получим:

M_z(F)=M_z(F_ху)=±F_ху·h*. (3.12)

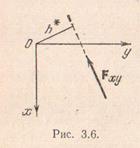Здесь h* – плечо силы F_ху относительно точки О. Если наблюдатель видит со стороны положительного направления оси z, что сила F_ху стремится повернуть тело вокруг оси z против хода часовой стрелки, то берется знак "+", и в противном случае – знак "–".

Формула (3.12) дает возможность сформулировать следующее правило для вычисления момента силы относительно оси. Для этого нужно:

· выбрать на оси произвольную точку и построить плоскость, перпендикулярную оси;

· спроектировать на эту плоскость силу;

· определить плечо проекции силы h*.

Момент силы относительно оси равен произведению модуля проекции силы на ее плечо, взятому с соответствующим знаком (см. изложенное выше правило).

Из формулы (3.12) следует, что момент силы относительно оси равен нулю в двух случаях:

· когда проекция силы на плоскость, перпендикулярную оси, равна нулю, т.е. когда сила и ось параллельны;

· когда плечо проекции h* равно нулю, т.е. когдалиния действия пересекает ось.

Оба эти случая можно объединить в один: момент силы относительно оси равен нулю тогда и только тогда, когда линия действия силы и ось находятся в одной плоскости.

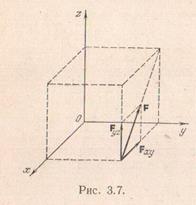
Задача 3.1.Вычислить относительно точки О момент силы F, приложеннойк точке А и направленной по диагонали грани куба со стороной а.

При решении подобных задач целесообразно сначала вычислить моменты силы Fотносительно координатных осей x, y, z. Координаты точки А приложения силы F будут

, , .

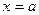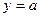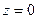Проекции силы Fна координатные оси:

, , .

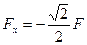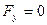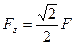Подставляя эти значения в равенства (3.10), найдем

, , .

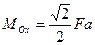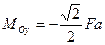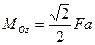Эти же выражения для моментов силы Fотносительно координатных осей можно получить, пользуясь формулой (3.12). Для этого спроектируем силу F на плоскости, перпендикулярные оси х и у. Очевидно, что 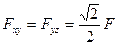. Применяя изложенное выше правило, получим, как и следовало ожидать, те же выражения:

, , .

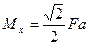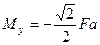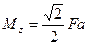Модуль момента определится равенством

.

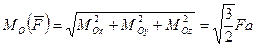Введем теперь понятие момента пары. Найдем сначала, чему равна сумма моментов сил, составляющих пару, относительно произвольной точки. Пусть О – произвольная точка пространства, а F и F' –силы, составляющие пару.

Тогда М_о(F)=ОА×F, М_о(F')=ОВ×F',

откуда

М_о(F)+ М_о(F')= ОА×F+ ОВ×F',

но так как F= -F', то

М_о(F)+ М_о(F')= ОА×F- ОВ×F=(ОА-ОВ)×F.

Принимая во внимание равенство ОА-ОВ=ВА, окончательно находим:

М_о(F)+ М_о(F')= ВА×F.

Следовательно, сумма моментов сил, составляющих пару, не зависит от положения точки, относительно которой берутся моменты.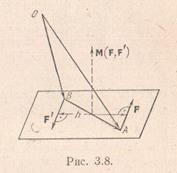

Векторное произведение ВА×Fи называется моментом пары. Обозначается момент пары символом М(F, F'), причем

М(F, F')= ВА×F= АВ×F',

или, короче,

М= ВА×F= АВ×F'. (3.13)

Рассматривая правую часть этого равенства, замечаем, что момент пары представляет собой вектор, перпендикулярный плоскости пары, равный по модулю произведению модуля одной сил пары на плечо пары (т.е. на кратчайшее расстояние между линиями действия сил, составляющих пару) и направленный в ту сторону, откуда "вращение" пары видно происходящим против хода часовой стрелки. Если h – плечо пары, то М(F, F')=h×F.

Из самого определения видно, что момент пары сил представляет собой свободный вектор, линия действия которого не определена (дополнительное обоснование этого замечания следует из теорем 2 и 3 этой главы).

Для того, чтобы пара сил составляла уравновешенную систему (систему сил, эквивалентную нулю), необходимо и достаточно, чтобы момент пары равнялся нулю. Действительно, если момент пары равен нулю, М=h×F, то либо F=0, т.е. нет сил, либо плечо пары h равно нулю. Но в этом случае силы пары будут действовать по одной прямой; так как они равны по модулю и направлены в противоположные стороны, то на основании аксиомы 1 они составят уравновешенную систему. Обратно, если две силы F₁иF₂, составляющие пару, уравновешены, то на основании той же аксиомы 1 они действуют по одной прямой. Но в этом случае плечо пары h равно нулю и, следовательно, М=h×F=0.

Теоремы о парах

Докажем три теоремы, с помощью которых становятся возможными эквивалентные преобразования пар. При всех рассмотрениях следует помнить, что они относятся к парам, действующим на какое-либо одно твердое тело.

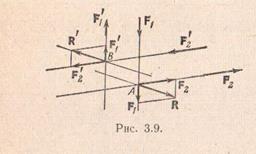Теорема 1. Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар.

Для доказательства этой теоремы рассмотрим две пары (F₁,F'₁) и (F₂,F'₂) и перенесем точки приложения всех сил вдоль линий их действия в точки А и В соответственно. Складывая силы по аксиоме 3, получим

R=F₁+F₂ и R'=F'₁+F'₂,

но F₁=-F'₁ и F₂=-F'₂.

Следовательно, R=- R', т.е. силы Rи R' образуют пару. Найдем момент этой пары, воспользовавшись формулой (3.13):

М=М(R, R')=ВА× R=ВА×(F₁+F₂)=ВА×F₁+ВА×F₂. (3.14)

При переносе сил, составляющих пару, вдоль линий их действия ни плечо, ни направление вращения пар не меняются, следовательно, не меняется и момент пары. Значит,

ВА×F₁=М(F₁,F'₁)=М₁, ВА×F₂= М(F₂,F'₂)=М₂

и формула (3.14) примет вид

М=М₁+М₂, (3.15)

что и доказывает справедливость сформулированной выше теоремы.

Сделаем два замечания к этой теореме.

1. Линии действия сил, составляющих пары, могут оказаться параллельными. Теорема остается справедливой и в этом случае, но для ее доказательства следует воспользоваться правилом сложения параллельных сил.

2. После сложения может получиться, что М(R, R')=0; на основании сделанного ранее замечания из этого следует, что совокупность двух пар (F₁,F'₁, F₂,F'₂)=0.

Теорема 2. Две пары, имеющие геометрически равные моменты, эквивалентны.

Пусть на тело в плоскости I действует пара (F₁,F'₁) с моментом М₁. Покажем, что эту пару можно заменить другой с парой (F₂,F'₂), расположенной в плоскости II, если только ее момент М₂равен М₁(согласно определению (см. 1.1) это и будет означать, что пары (F₁,F'₁) и (F₂,F'₂) эквивалентны). Прежде всего заметим, что плоскости I и II должны быть параллельны, в частности они могут совпадать. Действительно, из параллельности моментов М₁ и М₂(в нашем случае М₁=М₂) следует, что плоскости действия пар, перпендикулярные моментам, также параллельны.

Введем в рассмотрение новую пару (F₃,F'₃) и приложим ее вместе с парой (F₂,F'₂) к телу, расположив обе пары в плоскости II. Для этого, согласно аксиоме 2 нужно подобрать пару (F₃,F'₃) с моментом М₃ так, чтобы приложенная система сил (F₂,F'₂, F₃,F'₃) была уравновешена. Это можно сделать, например, следующим образом: положим F₃=-F'₁ и F'₃=-F₁и совместим точки приложения этих сил с проекциями А₁ и В₁ точек А и В на плоскость II. В соответствии с построением будем иметь: М₃= -М₁или, учитывая, что М₁= М₂,

М₂+М₃=0.

Принимая во внимание второе замечание к предыдущей теореме, получим (F₂,F'₂, F₃,F'₃)=0. Таким образом, пары (F₂,F'₂) и (F₃,F'₃) взаимно уравновешены и присоединение их к телу не нарушает его состояния (аксиома 2), так, что

(F₁,F'₁)= (F₁,F'₁, F₂,F'₂, F₃,F'₃). (3.16)

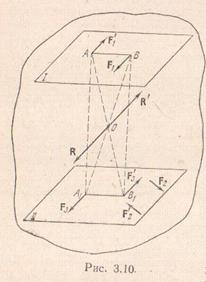С другой стороны, силы F₁ и F₃, а также F'₁ и F'₃ можно сложить по правилу сложения параллельных сил, направленных в одну сторону. По модулю все эти силы равны друг другу, поэтому их равнодействующие R и R' должны быть приложены в точке пересечения диагоналей прямоугольника АВВ₁А₁; кроме того, они равны по модулю и направлены в противоположные стороны. Это означает, что они составляют систему, эквивалентную нулю. Итак,

(F₁,F'₁, F₃,F'₃)=(R, R')=0.

Теперь мы можем записать

(F₁,F'₁, F₂,F'₂, F₃,F'₃)=(F₃,F'₃). (3.17)

Сравнивая соотношения (3.16) и (3.17), получим (F₁,F'₁)=(F₂,F'₂), что и требовалось доказать.

Из этой теоремы следует, что пару сил можно перемещать в плоскости ее действия, переносить в параллельную плоскость; наконец, в паре можно менять одновременно силы и плечо, сохраняя лишь направление вращения пары и модуль ее момента (F₁h₁= F₂h₂).

В дальнейшем мы будем широко пользоваться такими эквивалентными преобразованиями пары.

Теорема 3. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен сумме моментов двух данных пар.

Пусть пары (F₁,F'₁) и (F₂,F'₂) расположены в пересекающихся плоскостях I и II соответственно. Пользуясь следствием теоремы 2, приведем обе пары к плечу АВ, расположенному на линии пересечения плоскостей I и II. Обозначим трансформированные пары через (Q₁,Q'₁) и (Q₂,Q'₂). При этом должны выполняться равенства

М₁=М(Q₁,Q'₁)=М(F₁,F'₁) и М₂=М(Q₂,Q'₂)=М(F₂,F'₂).

Сложим по аксиоме 3 силы, приложенные в точках А и В соответственно. Тогда получим R=Q₁+Q₂и R'= Q'₁+Q'₂. Учитывая, что Q'₁=-Q₁и Q'₂=-Q₂, получим R=-R'. Таким образом , мы доказали, что система двух пар эквивалентна одной паре (R,R').

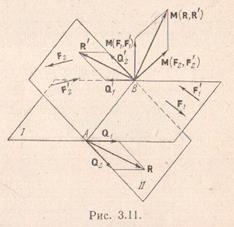Найдем момент Мэтой пары. На основании формулы (3.13) имеем

М(R,R')=ВА×(Q₁+Q₂)=ВА×Q₁+ВА×Q₂=

=М(Q₁,Q'₁)+М(Q₂,Q'₂)=М(F₁,F'₁)+М(F₂,F'₂)

или

М=М₁+М₂,

т.е. теорема доказана.

Заметим, что полученный результат справедлив и для пар, лежащих в параллельных плоскостях. По теореме 2 такие пары можно привести к одной плоскости, а по теореме 1 их можно заменить одной парой, момент которой равен сумме моментов составляющих пар.

Доказанные выше теоремы о парах позволяют сделать важный вывод: момент пары является свободным вектором и полностью определяет действие пары на абсолютно твердое тело. В самом деле, мы уже доказали, что если две пары имеют одинаковые моменты (следовательно, лежат в одной плоскости или в параллельных плоскостях), то они друг другу эквивалентны (теорема 2). С другой стороны, две пары, лежащие в пересекающихся плоскостях, не могут быть эквивалентны, ибо это означало бы, что одна из них и пара, противоположная другой, эквивалентны нулю, что невозможно, так как сумма моментов таких пар отлична от нуля.

Таким образом, введенное понятие момента пары чрезвычайно полезно, так как оно полностью отражает механическое действие пары на тело. В этом смысле можно сказать, что момент исчерпывающим образом представляет действие пары на твердое тело.

Для деформируемых тел изложенная выше теория пар неприменима. Две противоположные пары, действующие, например, по торцам стержня, с точки зрения статики твердого тела эквивалентны нулю. Между тем их действие на деформируемый стержень вызывает его кручение, и тем большее, чем больше модули моментов.

Перейдем к решению первой и второй задач статики, когда на тело действуют только пары сил.