Условия равновесия плоской системы сил

Как было установлено в главе 4, необходимым и достаточным условием равновесия системы сил является равенство нулю главного вектора и главного момента. Для плоской системы сил эти условия получают вид

F_О=∑F_k=0, М_Оz=∑ М_Оz(F_k)=0, (5.15) где О – произвольная точка в плоскости действия сил.

На основании (5.15) и (5.7) имеем

F_Ох=∑F_kх= F_1х+ F_2х … + F_пх=0,

F_Оу=∑F_kу= F_1у+ F_2у … + F_пу=0,

М_Оz=∑ М_Оz(F_k)= М_Оz(F₁)+ М_Оz(F₂)+ … + М_Оz(F_п)=0. (5.16) т.е. для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси и алгебраическая сумма моментов всех сил относительно произвольной точки равнялись нулю.

Возможны также другие формы уравнений равновесия.

Второй формой является равенство нулю алгебраических сумм моментов всех сил относительно любых трех точек, не лежащих на одной прямой:

∑ М_Аz(F_k)=0,

∑ М_Вz(F_k)=0,

∑ М_Сz(F_k)=0, (5.17)где А, В и С – указанные точки.

Необходимость выполнения этих трех равенств в случае равновесия системы сил вытекает из условия (5.15), и нам остается доказать их достаточность. Предположим, что все равенства (5.17) выполняются. Равенство нулю главного момента при центре приведения в точке А возможно, либо если система приводится к равнодействующей (R≠0) и линия ее действия проходит через точку А, либо R=0; аналогично равенство нулю главного момента относительно точек В и С означает, что либо R≠0 и равнодействующая проходит через обе точки, либо R=0. Но равнодействующая не может проходить через все эти три точки А, В и С (по условию они не лежат на одной прямой). Следовательно, равенства (5.17) возможны лишь при R=0, т.е. система сил находится в равновесии.

Заметим, что если точки А, В и С лежат на одной прямой, то выполнение условий (5.17) не будет достаточным условием равновесия, – в этом случае система может быть приведена к равнодействующей, линия действия которой проходит через эти точки.

Третьей формой уравнений равновесия плоской системы сил является равенство нулю алгебраических сумм моментов всех сил системы относительно двух любых точек и равенство нулю алгебраической суммы проекций всех сил системы на ось, не перпендикулярную прямой, проходящей через две выбранные точки:

∑ М_Аz(F_k)=0,

∑ М_Вz(F_k)=0,

∑ F_kх=0 (5.18) (ось х не перпендикулярна отрезку АВ).

Необходимость выполнения этих равенств для равновесия сил вытекает непосредственно из условий (5.15). Убедимся в том, что выполнение этих условий достаточно для равновесия сил.

Из двух равенств, как и в предыдущем случае, вытекает, что если система сил имеет равнодействующую, то ее линия действия проходит через точки А и В. Тогда проекция равнодействующей на ось х, не перпендикулярную отрезку АВ, оказывается отличной от нуля. Но эта возможность исключается третьим уравнением (так как R_х=∑ F_kх). Следовательно, равнодействующая должна равняться нулю и система находится в равновесии. Понятно, что если ось х будет перпендикулярна отрезку АВ, то уравнения (5.18) не будут достаточными условиями равновесия, так как в этом случае система может иметь равнодействующую, линия действия которой проходит через точки А и В.

Таким образом, система уравнений равновесия может содержать одно уравнение моментов и два уравнения проекций сил, либо два уравнения моментов и одно уравнение проекций, либо, наконец, три уравнения моментов.

Отметим, что при составлении любой из форм уравнений равновесия выбор координатных осей и точек, относительно которых берутся моменты сил, вообще говоря, произволен. Однако для получения более простых уравнений равновесия (каждое из которых содержит минимальное число неизвестных) целесообразно координатные оси проводить перпендикулярно неизвестным силам, а указанные точки выбирать на пересечении линий действия неизвестных сил.

При рассмотрении равновесия несвободного твердого тела на основании принципа освобождаемости заменяем действие связей их реакциями. Значит, если число заранее неизвестных реакций будет равно числу уравнений равновесия, в которых реакции входят, то задачу их определения можно выполнить. Если же число неизвестных реакций будет больше уравнений равновесия, то задача становится статически неопределенной.

Среди плоских задач статики особого рассмотрения заслуживает случай плоской системы параллельных сил. Хотя для этой системы главный вектор и главный момент по-прежнему определяются формулами (5.1) и (5.5), но вычисления значительно упрощаются.

Пусть линии действия всех сил параллельны оси у. Тогда уравнения равновесия для рассматриваемой системы параллельных сил будут

∑F_kу=0, ∑ М_Оz(F_k)=0. (5.19) В соответствии с (5.17) уравнения равновесия можно также записать в виде

∑ М_Аz(F_k)=0, ∑ М_Вz(F_k)=0, (5.20) причем точки А и В не должны лежать на прямой, параллельной оси у (если точки А и В будут лежать на прямой, параллельной оси у, то эти уравнения будут удовлетворяться при равнодействующей, отличной от нуля, если ее линия действия проходит через указанные точки).

Система сил, действующих на твердое тело, может состоять как из сосредоточенных (изолированных) сил, так и распределенных сил. Различают силы, распределенные по линии, по поверхности и по объему тела. Так, например, давление тяжелого цилиндрического катка на горизонтальную опорную поверхность представляет собой силы, распределенные вдоль линии (в данном случае – вдоль прямой). Давление газа на стенки сосуда может служить примером сил, распределенных по поверхности. Действие сил тяжести иллюстрирует случай сил, распределенных по объему тела.

Распределенные силы задаются их интенсивностью. Так, например, для объемных сил сначала вводится понятие средней интенсивности силы в окрестности рассматриваемой точки тела

.

Здесь – объем элемента, выделенного в окрестности точки, – сила, действующая на этот элемент. Тогда

называется интенсивностью силы, распределенной по объему в данной точке тела.

Аналогично вводится понятие интенсивности для силы, распределенной по поверхности и по длине линии:

,

,

где , 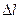– соответственно элементарная площадь и элемент длины линии.

Очень часто интенсивность силы называют силой, отнесенной к соответствующей геометрической единице – длине, площади или объему. Соответственно этому единицами интенсивности служат Н/м³, Н/м² и Н/м.

В простейших случаях интенсивность определяется простым делением полной силы давления на ее длину, площадь или объем участка ее приложения.

В ряде случаев силы оказываются равномерно распределенными. Так, давление воды на стенку плотины зависит от глубины, т.е. от координаты z. Давление сыпучего грунта на основание является функцией двух координат х и у из-за переменной толщины слоя.