Центры тяжести простейших фигур
 Центр тяжести треугольника.Воспользуемся способом разбиения и разделим треугольник АВС на элементарные полоски, проведя линии, параллельные стороне АС треугольника. Каждую такую полоску можно принять за прямоугольник; центры тяжести этих прямоугольников находятся в их серединах, т.е. на медиане BD треугольника. Следовательно, центр тяжести треугольника должен лежать на этой же медиане BD.
Центр тяжести треугольника.Воспользуемся способом разбиения и разделим треугольник АВС на элементарные полоски, проведя линии, параллельные стороне АС треугольника. Каждую такую полоску можно принять за прямоугольник; центры тяжести этих прямоугольников находятся в их серединах, т.е. на медиане BD треугольника. Следовательно, центр тяжести треугольника должен лежать на этой же медиане BD.
Разбивая теперь треугольник на элементарные полоски линиями, параллельными стороне АВ, заключаем, что центр тяжести треугольника должен быть расположен на медиане ЕС.
 Следовательно, центр тяжести треугольника находится в точке пересечения его медиан. Эта точка, как известно, делит каждую из медиан на отрезки в отношении
Следовательно, центр тяжести треугольника находится в точке пересечения его медиан. Эта точка, как известно, делит каждую из медиан на отрезки в отношении  , т.е
, т.е  .
.
Центр тяжести трапеции.Аналогично предыдущему, разобьем трапецию ABCD на элементарные полоски, параллельные основаниям ВС и АD. Центры тяжести полосок расположатся на прямой KL, соединяющей середины оснований трапеции. Следовательно, и центр тяжести трапеции лежит на этой прямой. Для того, чтобы найти его расстояние  от нижнего основания, разобьем трапецию на треугольники АВС и АСD. Для этих треугольников соответственно имеем
от нижнего основания, разобьем трапецию на треугольники АВС и АСD. Для этих треугольников соответственно имеем  ,
,  ,
,  ,
,  .
.
Используя формулу (8.20), получаем
 .
.
Центр тяжести дуги окружности. Рассмотрим дугу АDВ окружности радиуса  с центральным углом
с центральным углом  . Поместим начало координат в центре окружности и направим ось
. Поместим начало координат в центре окружности и направим ось  перпендикулярно хорде АВ.
перпендикулярно хорде АВ.
 Так как вследствие симметрии фигуры относительно оси
Так как вследствие симметрии фигуры относительно оси  центр тяжести будет лежать на этой оси
центр тяжести будет лежать на этой оси  , т.е.
, т.е.  , то остается только найти абсциссу центра тяжести
, то остается только найти абсциссу центра тяжести  ; для этого воспользуемся формулой (8.18).
; для этого воспользуемся формулой (8.18).
Согласно рис. имеем  ,
,  ,
,  и, следовательно,
и, следовательно,
 , (8.22) где
, (8.22) где 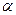 – половина центрального угла в радианах.
– половина центрального угла в радианах.
В частности, для дуги полуокружности  будем иметь
будем иметь
 .
.
Центр тяжести кругового сектора.Для определения положения центра тяжести кругового сектора разобьем его на элементарные секторы, как показано на рис. Каждый элементарный сектор можно принять за равнобедренный треугольник с высотой, равной  . Но высота в равнобедренном треугольнике является также и его медианой; следовательно, центр тяжести каждого элементарного треугольника лежит на расстоянии
. Но высота в равнобедренном треугольнике является также и его медианой; следовательно, центр тяжести каждого элементарного треугольника лежит на расстоянии  от начала координат О. Соответственно геометрическим местом центров тяжести всех элементарных треугольников является дуга окружности радиусом
от начала координат О. Соответственно геометрическим местом центров тяжести всех элементарных треугольников является дуга окружности радиусом  .
.
Это означает, что центр тяжести площади кругового сектора можно искать как центр тяжести материальной линии, по которой непрерывно и равномерно распределен вес этого сектора. Применив формулу (8.22), получим координату центра тяжести площади сектора
 , (8.23) где
, (8.23) где 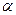 – половина центрального угла в радианах. В частности, для сектора в виде полукруга
– половина центрального угла в радианах. В частности, для сектора в виде полукруга  получим
получим
 . (8.24)
. (8.24)
Задача 8.3.Пластина получена из квадрата, сторона которого равна  , после того, как из него была вырезана часть, составляющая четверть круга радиуса
, после того, как из него была вырезана часть, составляющая четверть круга радиуса  с центром в вершине А квадрата. Определить центр тяжести пластины.
с центром в вершине А квадрата. Определить центр тяжести пластины.

Решение.Ось  проведем по диагонали квадрата, взяв начало оси в вершине А. Так как ось
проведем по диагонали квадрата, взяв начало оси в вершине А. Так как ось  является осью симметрии пластины, то центр тяжести ее находится на этой оси. Площадь квадрата без выреза
является осью симметрии пластины, то центр тяжести ее находится на этой оси. Площадь квадрата без выреза  , абсцисса его центра тяжести
, абсцисса его центра тяжести  ; площадь вырезанной части
; площадь вырезанной части  , абсцисса центра тяжести ее определяется формулой (8.23), в которой
, абсцисса центра тяжести ее определяется формулой (8.23), в которой  ,
,  :
:
 .
.
Центр тяжести пластины определим по формуле

или, подставляя соответствующие величины,
 .
.
Приведем без вывода формулы, определяющие положения центров тяжести некоторых простейших однородных тел.

