Графических метод получения линии тренда для одномерных процессов
Лабораторная работа № 4.1
Определение тенденции изменения многомерных процессов и прогнозирование их развития в Microsoft Excel
Цель работы: освоение методов получения регрессионных моделей, описывающих изменение экономических показателей, и их применение для определения тенденций их развития.
Задания, выполняемые в процессе работы
Задание № 1. Моделирование реальных данных и их идентификация. Задание состоит их двух этапов.
Этап 1. Моделирование реальных данных. Сводится к выполнению следующих действий:
а) столбцу А присвоить имя t. В диапазон ячеек А2:А20 ввести время измерения данных с шагом 1 сек, начиная со значения 0. Для генерации данных применить операцию копирования с помощью автозаполнения ячеек;
б) столбцу B присвоить имя r. В диапазон ячеек В2:В20 ввести значения согласно формуле =SIN(ПИ()*0,125*A2), используя операцию автозаполнения ячеек;
в) столбцу С присвоить имя e. В диапазон ячеек C2:C20 ввести значения, изменяющиеся по геометрической прогрессии с шагом 0,8. Первый член прогрессии равен 45;
г) столбцу Е присвоить имя y для получения выходной переменной. Диапазон ячеек E2:E20 заполнить значениями согласно формуле =2+4*B2-0,3*C2, используя операцию копирования данных с помощью процедуры автозаполнения ячеек;
д) столбцу F присвоить имя ey для моделирования помехи измерения выходной переменной y.Диапазон ячеек F2:F20 заполнить случайными числами, распределенными по нормальному закону. Помеха должна иметь нулевое среднее и стандартное отклонение 0,5. Для получения случайных данных применить раздел Генерация случайных чисел команды Анализ данных из меню Сервис;
е) столбцу G присвоить имя v для моделирования реальной выходной переменной y.Диапазон ячеек G2:G20 заполнить данными с помощью формулы v= y + ey;
ж) построить диаграмму типа график зависимости v=f(t) (назовем эту область График1).
На этом заканчивается первый этап выполнения задания.
Этап 2. Построение математической модели. В качестве входа использовать переменные r и e, выхода — v. Выполнить следующие действия:
з) с помощью раздела Регрессия команды Анализ данных из меню Сервисполучить оценки параметров линейной модели;
и) сравнить полученные оценки параметров с эталонными значениями, заданными на этапе 1, и привести обоснование их различия;
к) оценить качество полученной модели по критерию R2;
л) столбцу H присвоить имя vprog для получения прогноза выходной переменной v.Диапазон ячеек H2: H20 заполнить значениями, используя уравнение линейной регрессии с полученными оценками параметров в качестве формулы;
м) добавить полученный ряд данных vprog в графическую область График1;
н) используя функцию ТЕНДЕНЦИЯ, в ячейки Н21, Н22 разместить значения прогноза изменения переменной v для моментов времени t=21, 22 сек;
о) добавить полученные значения vprog для моментов времени t=21, 22 сек в графическую область График1.
На этом заканчивается этап 2.
Составить отчет по результатам выполнения задания.
Варианты задания.
1. Выполнить первый этап задания. На шаге д) для моделирования помехи примерить функцию СЛЧИС() для получения случайной величины, изменяющейся в интервале [0,2; 0,4]. На втором этапе на шаге з) для определения оценок параметров регрессионной модели применить функцию ЛИНЕЙН.
2. На шаге в) этапа 1 сгенерировать переменную е согласно закону
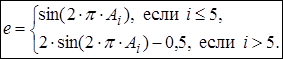
3. Определить регрессионную модель вида y=f(r, e).
4. Найти линию тренда между v и r. Построить графики зависимости v=f(r). Добавить линию тренда и вывести критерий адекватности. Если необходимо, то провести обработку данных с тем чтобы критерий был не ниже 0,9.
5. Реализовать этап 1 задания1. Затем выполнить следующие действия:
а) построить график изменение переменной v(t);
б) добавить к имеющейся диаграмме экспоненциальную линию тренда;
в) определить ошибку прогнозирования переменной v с помощью полученной линии тренда;
г) получить значения линии тренда с помощью процедуры экспоненциального сглаживания команды Анализ данных меню Сервис. Подобрать константу сглаживания;
д) определить ошибку прогнозирования переменной v с помощью полученной линии тренда;
е) определить качество работы полученных моделей прогнозирования и сделать выводы по практическому их применению;
ж) добавить к имеющейся диаграмме новую линию тренда и дать прогноз на два интервала времени вперед.
Лабораторная работа № 4.2
Графических метод получения линии тренда для одномерных процессов
Цель работы: освоение графического метода получения линии тренда для одномерных процессов и ее применение для определения тенденций развития процесса.
Задача. Пусть известна мощность P и площадь обогрева S для каждого момента времени t (табл. 1). Известны затраты на обогрев Z. Необходимо построить линейную математическую модель Z=f(S).
Таблица 1.
Исходные данные для получения регрессионной модели
