Теоретичні відомості про параболу
Параболою називається геометричне місце точок, кожна з яких однаково віддалена від заданої фіксованої точки (фокуса) і від заданої фіксованої прямої (директриси). Найпростіше рівняння параболи має вигляд: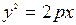 
, де 
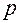- параметр, тобто відстань між директрисою та фокусом. Рівняння директриси 
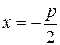, фокус – це точка 
.
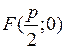Є випадки задання параболи:
1) 
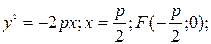
2) 
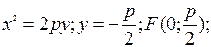
3) 
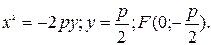
Рівняння парабол зі зміщеною вершиною мають вигляд:
; 
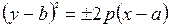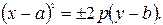
Задача № 4. Скласти рівняння параболи з вершиною в початку координат, знаючи координати фокуса (-2;0).
Задача № 5. Визначити координати вершини і величину параметра параболи, рівняння якої: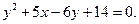 
Знайти також координати її фокуса і рівняння директриси параболи
Питання для самоперевірки знань, умінь
1. Що називається колом? Що таке центр кола, радіус кола?
2. Що називається еліпсом? Пояснити, чому еліпс є лінією другого порядку?
3. Що таке ексцентриситет еліпса?
4. Як пов’язаний еліпс з колом?
5. Що називається гіперболою? Осі гіперболи, фокуси, вершини.
6. Канонічне рівняння гіперболи. Спряжені гіперболи.
7. Яка гіпербола називається рівносторонньою ?
8. Ексцентриситет гіперболи.
9. Рівняння асимптот гіперболи.
10. Що таке парабола? Вершина параболи, фокус, параметр.
11. Що називається директрисою параболи? Рівняння директриси параболи.
12. Як визначити вершину параболи та її параметр, якщо задано рівняння параболи ?
Висновок__________________________________________________
Перевірив викладач ___________ Оцінка __________ Дата ___________
Виконаємо самостійно
В-1 В-2
1. Скласти рівняння кола з центром в точці С, яке проходить через
точку А
С(3;-2); A(6;2) С(3;-5 ); A(0;-1)
2. Звести рівняння кола до канонічного вигляду:
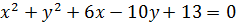
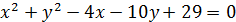
3. Скласти рівняння радіуса даного кола, проведеного в дану на ньому точку М
,
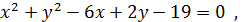
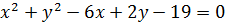M(5;-6) M(6;3)
4. Дано еліпс
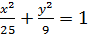
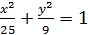
Знайти довжини осей, координати вершин, фокусів, ексцентриситет еліпса.
5. Знайти координати вершин, фокусів, ексцентриситет та асимптоти гіперболи
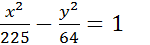
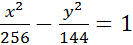
6. Скласти рівняння гіперболи за координатами її фокусів і ексцентриситетом
F12(±5;0); e 
F12(±10;0); e
7. Скласти рівняння параболи, якщо:
її фокус в точці F(0;4) рівняння директриси x= - 3.
В-3 В-4
1. Скласти рівняння кола з центром в точці С, яке проходить через
точку А
С(2;-1); A(5;3) С(-4;0); A(4;-6)
2. Звести рівняння кола до канонічного вигляду:
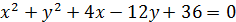
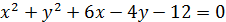
3. Скласти рівняння радіуса даного кола, проведеного в дану на ньому точку М
,
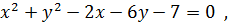
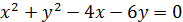M(2;-1) M(-1;1)
4. Дано еліпс
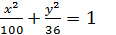
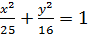
Знайти довжини осей, координати вершин, фокусів, ексцентриситет еліпса.
5. Знайти координати вершин, фокусів, ексцентриситет та асимптоти гіперболи
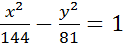
6. Скласти рівняння гіперболи за координатами її фокусів і ексцентриситетом
F12(±5;0); e F12(±10;0); e
7. Скласти рівняння параболи, якщо:
її фокус в точці F(-4;0) рівняння директриси y = 3.
ТЕМА 3. ВСТУП ДО МАТЕМАТИЧНОГО АНАЛІЗУ
ПРАКТИЧНА РОБОТА № 6