Теорема об изменении кинетического момента
Для материальной точки массой 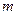 , движущейся со скоростью
, движущейся со скоростью 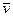 , кинетическим моментом
, кинетическим моментом 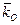 относительно какого-либо центра
относительно какого-либо центра 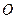 называют момент количества движения точки относительно этого центра
называют момент количества движения точки относительно этого центра 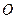 , т. е.
, т. е.
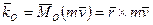 . (168)
. (168)
Кинетический момент 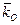 приложен к точке
приложен к точке 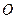 , относительно которой он вычисляется.
, относительно которой он вычисляется.
Проецируя обе части (168) на прямоугольные декартовы оси, получаем кинетические моменты точки относительно этих осей координат, если точка 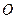 является началом осей координат:
является началом осей координат:
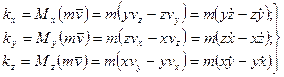 (168')
(168')
Для механической системы кинетическим моментом 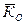 (или главным моментом количества движения системы относительно какой-либо точки
(или главным моментом количества движения системы относительно какой-либо точки 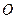 ) называют векторную сумму кинетических моментов точек этой системы, взятых относительно точки
) называют векторную сумму кинетических моментов точек этой системы, взятых относительно точки 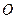 , т. е.
, т. е.
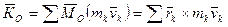 . (169)
. (169)
Кинетический момент системы 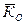 приложен к точке
приложен к точке 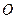 , относительно которой он вычисляется.
, относительно которой он вычисляется.
Если спроецировать (168) на прямоугольные декартовы оси координат, то получим проекции кинетического момента на эти оси, или кинетические моменты относительно осей координат:
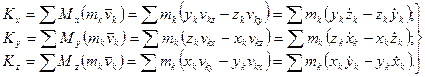
Кинетический момент твердого тела относительно оси вращения, когда тело вращается вокруг этой неподвижной оси 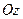 с угловой скоростью
с угловой скоростью 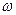 равен:
равен:
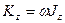 . (170)
. (170)
Таким образом, кинетический момент тела относительно оси вращения при вращательном движении равен произведению угловой скорости тела на его момент инерции относительно оси вращения. Знак кинетического момента относительно оси совпадает со знаком угловой скорости вращения вокруг этой оси: при вращении против часовой стрелки кинетический момент положительный; при вращении по часовой стрелке – отрицательный.
Формулы для кинетических моментов относительно двух других осей координат 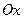 и
и 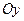 перпендикулярных оси вращения
перпендикулярных оси вращения 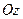 :
:
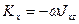 ,
, 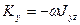 ,
,
где 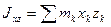 ,
, 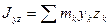 – центробежные моменты инерции.
– центробежные моменты инерции.
Теорема об изменении кинетического момента точки
Первая производная по времени от кинетического момента точки относительно какого-либо центра равна моменту силы относительно того же центра:
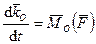 . (171)
. (171)
Проецируя (171) на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента точки относительно этих осей координат:
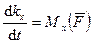 ,
, 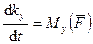 ,
, 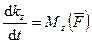 . (171')
. (171')
Теорема об изменении кинетического момента системы
Первая производная по времени от кинетического момента системы относительно какой-либо точки равна векторной сумме моментов внешних сил, действующих на систему, относительно той же точки.
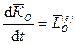 , (172)
, (172)
где 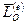 – главный момент всех внешних сил системы.
– главный момент всех внешних сил системы.
Проецируя (172) на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента системы относительно этих осей координат, т. е.
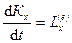 ,
, 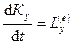 ,
, 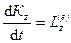 . (172')
. (172')
