Общая теория комплексных чисел

Задание {{ 161 }} ТЗ № 161

Отметьте правильный ответ

Поле комплексных чисел является расширением

R Поля вещественных чисел

£ Поля рациональных чисел

£ Кольца вещественных чисел

£ Кольца рациональных чисел

Задание {{ 162 }} ТЗ № 162

Отметьте правильный ответ

Алгебраическая форма записи комплексного числа имеет вид:

£

£

£

R

Задание {{ 163 }} ТЗ № 163

Отметьте правильный ответ

Комплексные числа и называются …

£ обратными

£ противоположными

R сопряженными

£ симметричными

Задание {{ 164 }} ТЗ № 164

Отметьте правильный ответ

Два комплексных числа в тригонометрической форме равны, если …

£ Их модули равны

£ Их аргументы равны

R Их модули равны и аргументы отличаются на целочисленное кратное

£ Их модули отличаются на целочисленное число к

Задание {{ 165 }} ТЗ № 165

Отметьте правильный ответ

Корни n-ой степени из 1 вычисляются по формуле

R

£

£

£

Задание {{ 166 }} ТЗ № 166

Отметьте правильный ответ

В алгебраической форме записи комплексного числа

£ i – мнимая единица и

R а - вещественная часть, - мнимая часть, 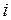- мнимая единица и

£ b - вещественная часть, a - мнимая часть,

£ a - вещественная часть, b - мнимая часть, и

Задание {{ 167 }} ТЗ № 167

Отметьте правильный ответ

Тригонометрическая форма комплексного числа имеет вид:

R

£

£

£

Задание {{ 168 }} ТЗ № 168

Отметьте правильный ответ

Пусть и что из перечисленного верно?

£

R

R

Задание {{ 169 }} ТЗ № 169

Отметьте правильный ответ

Формула Муавра имеет вид:

£

£

R

£

Задание {{ 170 }} ТЗ № 170

Отметьте правильный ответ

Аргумент комплексного числа при равен:

R

£ 0

£ Не определен

£ Единице

Задание {{ 171 }} ТЗ № 171

Отметьте правильный ответ

Произведение двух корней n- ой степени из единицы есть:

£

£ Единице

£ Нуль

R Корень n – ой степени из 1

Задание {{ 172 }} ТЗ № 172

Отметьте правильный ответ

Корень n-ой степени из 1 называется первообразным корнем n- ой степени из 1. если …

£ , но , при

£ , но , при

R , но , при

£ , но , при

Задание {{ 173 }} ТЗ № 173

Отметьте правильный ответ

Аргумент произведения двух комплексных чисел равен:

R Сумме аргументов этих чисел

£ Произведению аргументов этих чисел

£ Частному аргументов этих чисел

£ Разности аргументов этих чисел

Задание {{ 174 }} ТЗ № 174

Отметьте правильный ответ

В алгебраической записи комплексного числа число а называют вещественной частью и обозначают:

R Re z

£

£ Im z

£

Задание {{ 175 }} ТЗ № 175

Отметьте правильный ответ

Модуль произведения двух комплексных чисел равен:

£ Единице

£ Сумме комплексных чисел

£ Сумме произведения сомножителей

R Произведению модулей сомножителей

Задание {{ 176 }} ТЗ № 176

Отметьте правильный ответ

Аргумент частного двух комплексных чисел равен:

£ Сумме аргументов делимого и делителя

£ Частному модулей делимого и делителя

R Разности аргументов делимого и делителя

£ Произведению модулей этих чисел

Задание {{ 177 }} ТЗ № 177

Отметьте правильный ответ

В алгебраической записи комплексного числа число b называют мнимой частью и обозначают:

£ Re z

£

£

R Im z

Задание {{ 178 }} ТЗ № 178

Отметьте правильный ответ

Если - первообразный корень n-ой степени из единицы, то число будет первообразным корнем n-ой степени, если:

R к взаимно простое с n

£ n – простое число

£ к – простое число

£ при делении к на n получим остаток равный 1

Задание {{ 179 }} ТЗ № 179

Отметьте правильный ответ

Что из перечисленного верно, если

R

R вещественное число

£

Задание {{ 180 }} ТЗ № 180

Отметьте правильный ответ

Какая из формул правильная?

£

R

£