Математическое моделирование и решение экономических задач
Целью является формирование:
1. Способности работать самостоятельно, забота о качестве, стремление к успеху (ОК-6)
2. Способности порождать новые идеи (ОК-5)
3. Умения ориентироваться в современных алгоритмах компьютерной математики, совершенствовать, углублять и развивать математическую теорию, лежащую в их основе (ПК-7)
4. Умения делать самостоятельный анализ физических аспектов в классических постановках математических задач (ПК-4)
5. Умения определять общие формы закономерностей, инструментальных средств для групп дисциплин (ПК-10)
Теоретические основы
В общем виде задача линейного программирования формулируется так: надо найти величины x1, x2, … xn доставляющие максимум (или минимум) некоторой линейной функции
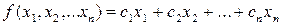
и удовлетворяющей ограничениям вида
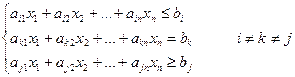
Среди этих ограничений часто встречаются условия неотрицательности всех или части переменных: 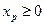 . Вообще-то эти условия являются частным случаем условий общего вида, но, по традиции, их выделяют в отдельную группу.
. Вообще-то эти условия являются частным случаем условий общего вида, но, по традиции, их выделяют в отдельную группу.
Функция 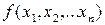 называется целевой функцией.
называется целевой функцией.
1) Графический способ решения задачи линейного программирования в случае двух переменных.
Для случая двух переменных задача записывается:
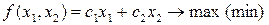
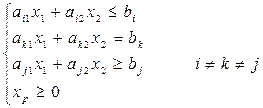
Геометрическая интерпретация вышеприведенных ограничений ясна: на плоскости x1 x2 эти неравенства и уравнения образуют некоторую область – многоугольник. Требуется найти максимальное (минимальное) значение целевой функции при значениях переменных, не выходящих за пределы многоугольника.
К числу основных постулатов метода относится утверждение, что максимум (минимум) целевой функции может быть достигнут только в одной из вершин многоугольника. Пара координат вершины называется опорным решением.
Линиями уровня целевой функции 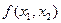 называют семейство прямых
называют семейство прямых 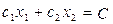 , где С – произвольная постоянная. Чем больше значение константы С, тем правее и выше расположена соответствующая прямая.
, где С – произвольная постоянная. Чем больше значение константы С, тем правее и выше расположена соответствующая прямая.
Графический способ решения задачи линейного программирования заключается в том, чтобы, проводя линии уровня целевой функции последовательно через все вершины многоугольника, определить такую из них, что дальнейшее продвижение линии уровня без выхода за пределы многоугольника оказалось бы невозможным. Тогда координаты этой вершины и доставят целевой функции максимально (минимально) возможное значение.
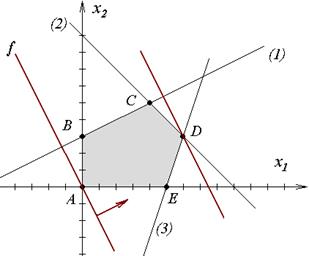 Рис.5 Рис.5 |
С точки зрения экономической интерпретации, задача линейного программирования может быть истолкована как задача о максимизации доходов (целевая функция) некоторого предприятия, выпускающего несколько видов различной продукции, и обладающего определенными запасами сырья (система ограничений).
Пример. Найти максимум целевой функции при заданной системе ограничений.
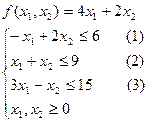
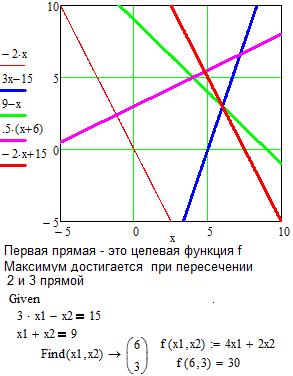 Выпишем неравенства в виде уравнений, и построим полученные прямые на плоскости x1x2. Очевидно, что в результате получаем заштрихованную область – пятиугольник ABCDE (рис.5). Кроме того, строим целевую функцию f. Строя линии уровня для целевой функции, приходим к положению, когда дальнейшее продвижение прямой, соответствующей целевой функции дальше вправо невозможно. Это произойдет тогда, когда целевая функция пройдет через точку D. Очевидно, координаты этой точки D и доставят целевой функции искомый максимум. Эти координаты получим из решения системы двух уравнений, соответствующих второй и третьей прямой – прямые (2) и (3) на графике. Легко видеть, что точка пересечения D имеет координаты (6,3). Подставляя найденные значения в целевую функцию, получим ее максимальную величину
Выпишем неравенства в виде уравнений, и построим полученные прямые на плоскости x1x2. Очевидно, что в результате получаем заштрихованную область – пятиугольник ABCDE (рис.5). Кроме того, строим целевую функцию f. Строя линии уровня для целевой функции, приходим к положению, когда дальнейшее продвижение прямой, соответствующей целевой функции дальше вправо невозможно. Это произойдет тогда, когда целевая функция пройдет через точку D. Очевидно, координаты этой точки D и доставят целевой функции искомый максимум. Эти координаты получим из решения системы двух уравнений, соответствующих второй и третьей прямой – прямые (2) и (3) на графике. Легко видеть, что точка пересечения D имеет координаты (6,3). Подставляя найденные значения в целевую функцию, получим ее максимальную величину 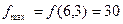 . Итак: целевая функция достигает максимума при x1=6, x2=3, и этот максимум равен 30.
. Итак: целевая функция достигает максимума при x1=6, x2=3, и этот максимум равен 30.
Решение этой задачи в пакете MathCad будет иметь вид:
Замечание: надо отметить, что для того, чтобы существовал максимум целевой функции в некоторой область, эта область должна быть замкнута сверху. Если область сверху неограниченна, то целевая функция не имеет конечного максимума. То же самое относится к минимуму, с поправкой, что область должна быть ограничена снизу (рис.6).
На рисунке показаны области неограниченные сверху или снизу.
