Классификация автоматических систем. Примеры по классификации

СПИСОК ВОПРОСОВ

1.Классификация автоматических систем. Примеры по классификации.

2.Методы анализа линейных систем радиоавтоматики.

3.Характеристики линейных систем радиоавтоматики, связь между ними.

4.Структурные схемы, отличие от функциональных. Примеры.

5.Инерционные и интегрирующие звенья, их характеристики.

6.Дифференцирующие и упругие звенья, их характеристики.

7.Форсирующее и колебательное звенья, их характеристики.

8.Передаточные функции разомкнутых и замкнутых систем, передаточные функции ошибки от регулирующего и возмущающего воздействий.

9.Устойчивость линейных САУ. Теорема Ляпунова. Критерий Гурвица.

10.Частотный критерий Найквиста. Примеры.

11.Частотный критерий Михайлова. Примеры.

12.Качество регулирования в установившемся и вынужденном режимах. Примеры.

13.Связь между структурой системы, входным воздействием и ошибкой регулирования. Примеры.

14.Качество переходных режимов, методы определения параметров качества.

15.Аналитический способ определения переходной характеристики.

16.Определения параметров переходного режима с помощью ЛАЧХ.

17.Классификация нелинейных систем, примеры.

18.Методы анализа нелинейных систем.

19.Система термостатирования. Структурная схема, дифф. уравнения.

20.Фазовый метод анализа нелинейных систем. Правила вычерчивания фазовых траекторий.

21.Фазовый портрет системы термостатирования.

22.Гармоническая линеаризация.

23.Метод Гольдфарба, примеры.

24.Связь между диаграммой Гольдфарба и фазовым портретом системы. Примеры.

25.Основные характеристики случайных процессов.

26.Теорема Винера - Хинчина.

27.Случайные процессы в линейных системах радиоавтоматики.

28.Ошибки регулирования в системах радиоавтоматики при случайном управляющем воздействии.

29.Ошибки регулирования в системах радиоавтоматики при одновременном воздействии случайного управляющего сигнала и помехи.

Вопрос 1

Классификация автоматических систем. Примеры по классификации

Классификация автоматических систем

1. По качеству регулирования

а) системы с регулированием по возмущению (без обратной связи)

Система автоматического регулирования усиления:

1 каскад

2 каскад

3 каскад

Амплитудный детектор

>

Uвых

Uвых

Uвх

Без АРУ

Достоинства этой системы в простоте и отсутствии склонности к самовозбуждению. Недостаток: низкое качество регулирования по сравнению с системами с ОС.

Регулирующее воздействие вырабатывается на основе анализа внешних воздействий, действующих на систему. Анализ состояния объекта не производится.

б) система с регулированием по отклонению (с ОС)

1 каскад

2 каскад

3 каскад

Амплитудный детектор

>

Uвых

Uрег = Uвых

Uвых

Uвх

Достоинство – высокое качество регулирования. Недостаток: склонность к самовозбуждению.

Регулирующее воздействие вырабатывается на основе информации о действительном состоянии объекта регулирования в сравнении с требуемым.

2. а) системы стабилизации

Необходимы для поддержания параметров регулируемого объекта на постоянном уровне.

Упрощенная схема системы стабилизации скорости ленты в аудио (видео) магнитофоне:

двигатель

>

Частотный детектор

>

Головка синхронизации

f эталонная (из сети переменного напряжения)

(замкнутая система стабилизации через ленту).

б) следящая система

Это система, которая изменяет состояние объекта регулирования по какому-то заданному закону (определяется внешним управляющим сигналом).

Такая система есть в каждом дисководе.

э/м двигатель

>

лазер

датчик

ξ – разностное напряжение

дорожка

в) система программного регулирования

Когда состояние объекта регулирования изменяется про закону, заданному программой.

Такая система поворачивает спутниковую антенну.

программа

часы

двигатель

>

-

ξ

редуктор

датчик

3. а) Статические системы

Ошибка регулирования является источником формирования регулирующего воздействия, поэтому ошибка всегда есть.

Система статической автоматической подстройки частоты:

Смеситель

УПЧ

Частотный дискриминатор

fс

УПТ

Гетеродин

fпр

Uд

Uупр

fг

УПЧ

f

fпр1

Uд

fпр

fпр1

ЧД

Велика опасность самовозбуждения.

б) астатическая система

УРЧ

Смеситель

УПЧ

УПТ

Двигатель постоянного тока

Гетеродин

Вместо варикапа используется механически перестраиваемый конденсатор переменной ёмкости.

Двигатель перестанет работать, когда на УПТ U=0, следовательно, происходит точная настройка на f_пр1.

Астатическая система включает в себя интегрирующие звенья.

Вопрос 2

Методы анализа линейных систем радиоавтоматики

Линейная система – система, которая описывается линейными дифференциальными уравнениями. Стационарная линейная система описывается линейным дифференциальным уравнением с постоянными коэффициентами (не меняющиеся во времени частоты, уровни и т.д.).

Следящая система

x

y

Y копирует x. ДУ такой системы:

.

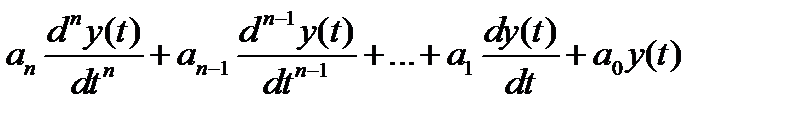Все методы анализа линейной системы основаны на методе суперпозиции:

.

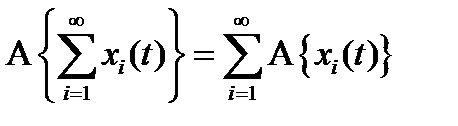A

x

y

x – состояние регулируемого объекта,

y – фактическое состояние (датчик),

A – оператор, функция (K(jω), K(p), g(t), h(t)).

Метод Фурье:

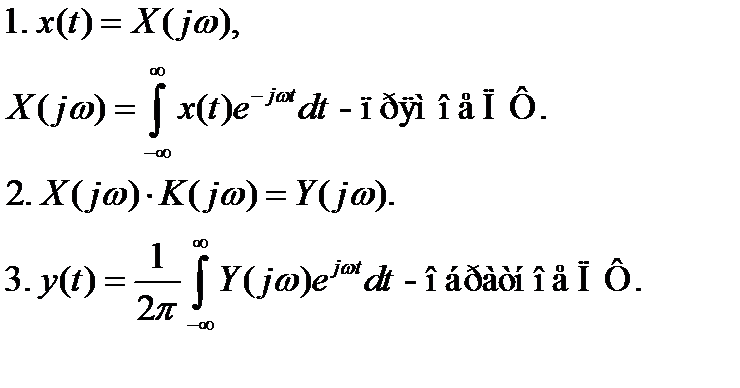
Изображение по Лапласу:

X(p) – изображение (спектр комплексной частоты Лапласа).

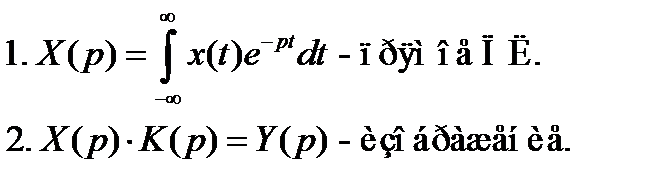
K(p) – частотная характеристика системы в области комплексной частоты (передаточная функция).

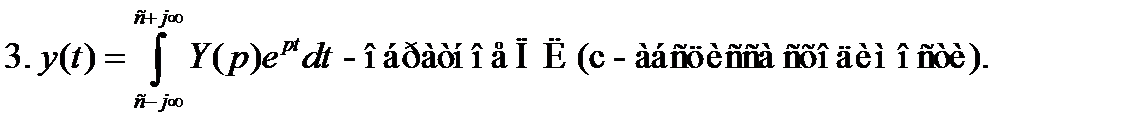
Дюамель:

Δt→0

t

y(t)

t

x(t)

Импульсная характеристика:

t

g(t)

t

y(t)

t

h(t)

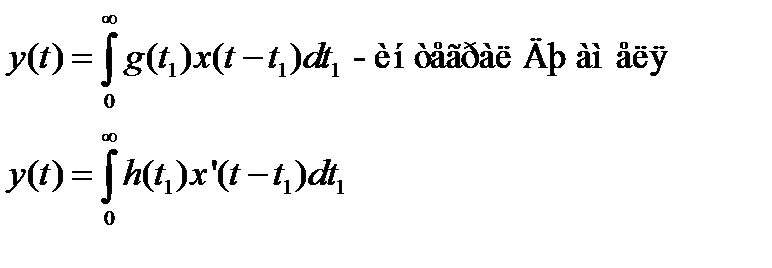
Вопрос 3

Характеристики линейных систем радиоавтоматики, связь между ними

Основные характеристики ЛС: K(jω), K(p), g(t₁), h(t₁).

1. Связь между передаточной функцией и комплексным коэффициентом передачи:

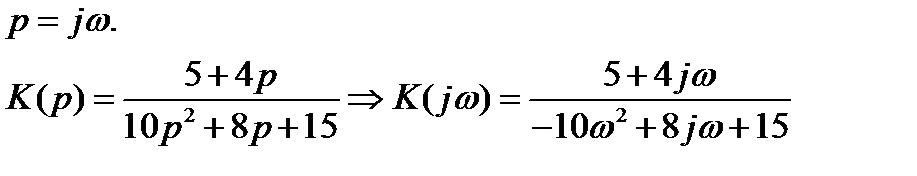
2. Связь между временными и частотными характеристиками K(jω) и g(t) – прямое и обратное преобразование Фурье:

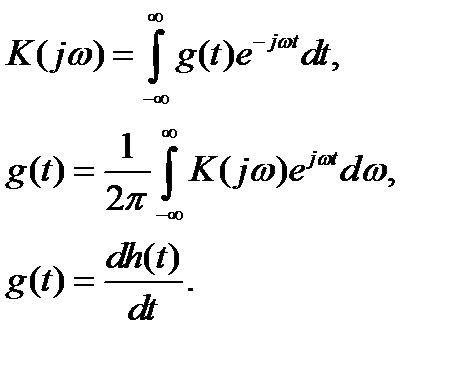
Дифференциальное уравнение:

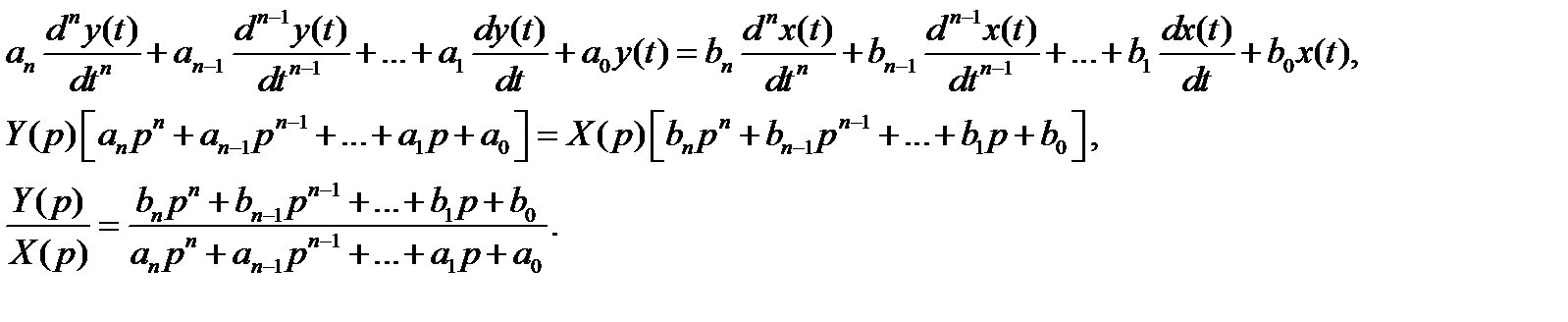
Передаточная функция системы есть отношение полиномов (коэффициенты в числителе - из правой части ДУ, в знаменателе – из левой части ДУ).

К(p)

X(p)

Y(p)

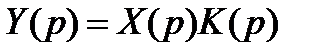
АЧХ=геом сумма от K(jw) ФЧХ=arctg(Im/Re) Годограф-Кривая, нарисованная концом вектора компл коэф-та передачи при изменении частоты от 0 до 00

Логарифмическая АЧХ

Вопрос 4

Структурные схемы, отличие от функциональных. Примеры

Структурные схемы – набор прямоугольников, соединённых стрелками, показывающих направление распространения информации. В прямоугольниках указываются соответствующие передаточные функции.

Структурные звенья 1^го порядка:

.

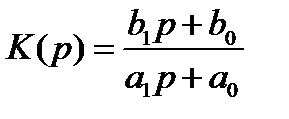1. Безынерционное (пропорциональное) звено

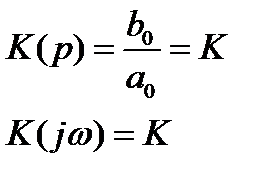
K(ω)

ω

2. Инерционное

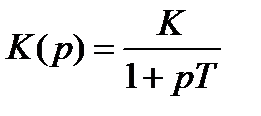
K – коэффициент усиления на постоянном токе, T – постоянная времени инерционного звена.

K(ω)

ω

Im

Re

K

3. Идеальное интегрирующее

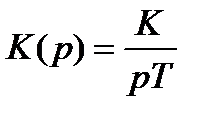
K(ω)

ω

Im

Re

4. Дифференцирующее

а) идеальное дифференцирующее звено

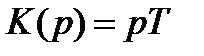
K(ω)

ω

Im

Re

5. Реальное дифференцирующее звено

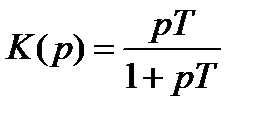
K(ω)

ω

Im

Re

5. Упругие звенья

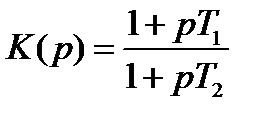
а) T₁ > T₂ – упругое дифференцирующее

K(ω)

ω

Im

Re

б) T₁ < T₂ – упругое интегрирующее

K(ω)

ω

Im

Re

6. Форсирующее

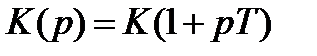
K(ω)

ω

K

Im

Re

K

7. Колебательное

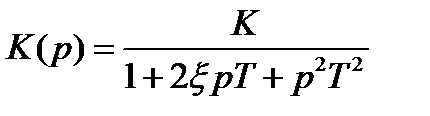
K(ω)

ω

K

1/T

Im

Re

В структурных схемах используется операторный метод. В качестве описания используется передаточная функция каждого элемента. Функциональные схемы позволяют рассмотреть схему на уровне принципа работы и связей между основными элементами.

Вопрос 5

Инерционные и интегрирующие звенья, их характеристики

Инерционные звенья

.

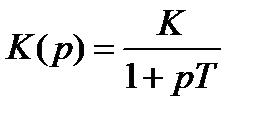K – коэффициент усиления на постоянном токе.

T – постоянная времени инерционного звена.

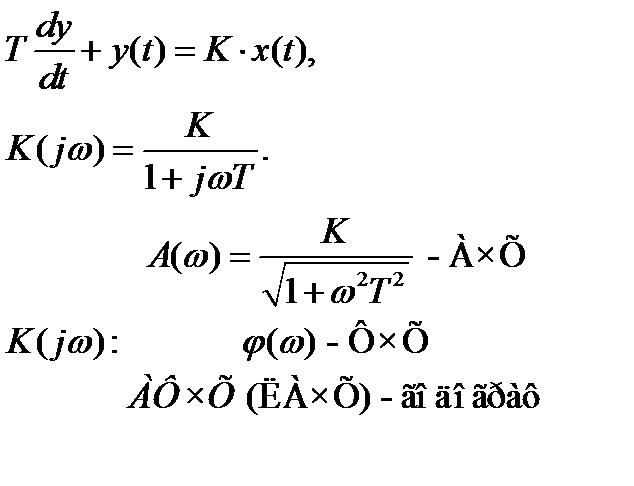
A(ω)

ω

φ(ω)

ω

φ(ω) = 0 - arctg(ωt) = - arctg(ωt).

Im

Re

K

L(ω), дБ

ω

3 дБ

ωр

.

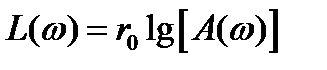Интегрирующие звенья:

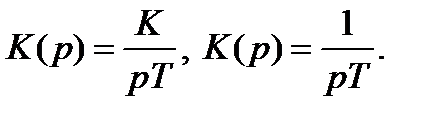
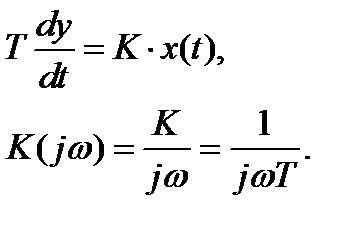
A(ω)

ω

φ(ω)

ω

-π/2

Im

Re

L(ω), дБ

ω

ωр

Подадим на вход ступеньку, получаем

t

h

Сравним с инерционным звеном.

R

C

R

C

h(t) = 1-e-1/T

- интегрирующий операционный усилитель

К интегрирующему операционному усилителю предъявляются требования:

K→ ∞,

R_вх → ∞,

R_вых→ ∞.

Инерционность появляется сама из-за наличия паразитных параметров.

Вопрос 6

Дифференцирующие и упругие звенья, их характеристики

1. Дифференцирующие звенья

K(jω): A(ω) – АЧХ, φ(ω) – ФЧХ, АФЧХ – годограф, ЛАЧХ.

а) идеальное дифференцирующее звено

K(p) = pT, y(t)=Tdx/dt.

A

ω

φ

ω

π/2

Im

Re

A

lg ω

1/T

-20дБ/дек

L(ω) = 20lg(ωT).

Подадим единичный импульс.

K(p)

1(t)

1/p

h(t)

K(p)/p

.

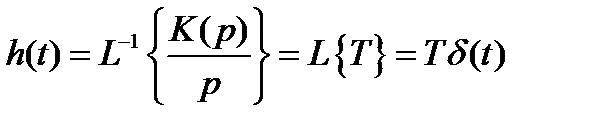Импульсная характеристика имеет вид:

Im

Re

Операционный дифференциальный усилитель:

R

C

- дифференцирующий операционный усилитель

Требования к ОУ: K = -∞, R_вх → ∞, R_вых → 0

Область применения: коррекция автоматических систем.

б) реальное дифференцирующее звено

.

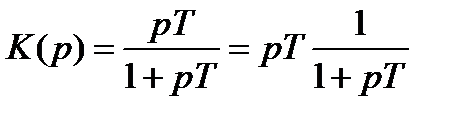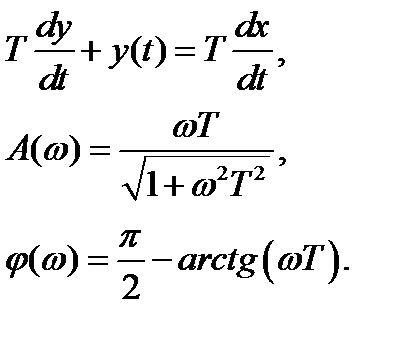
K(ω)

ω

φ(ω)

ω

π/2

Im

Re

L(ω)

ω

1/T

.

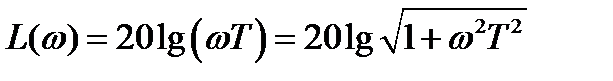Область применения: коррекция автоматических систем.

Дифференцирующие звенья поглощают астатизм и являются «противоположными» интегрирующим.

Самая простая реализация вынужденной схемы:

R

C

Переходная характеристика:

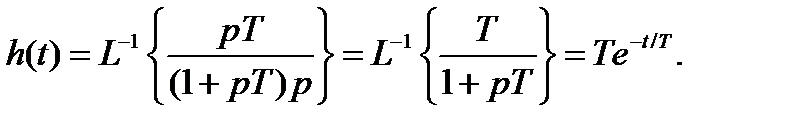
h(t)

t

T1

T2

T3

T1>T2>T3

Чем больше постоянная времени, тем выше качество дифференцирования.

2. Упругие звенья

Передаточная характеристика:

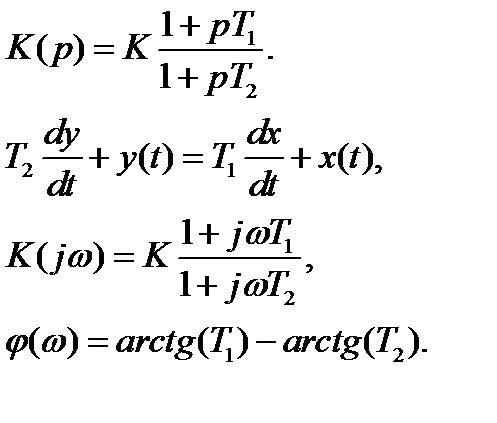
Возможны два варианта:

а) T₁ > T₂ (звено упругое дифференцирующее);

б) T₂ > T₁ (звено упругое интегрирующее).

T1/T2

T1/T2

а)

б)

K

ω

A(ω)

а)

б)

ω

φ(ω)

а)

б)

Re

Im

T1/T2

T1/T2

а)

а)

R

C

R

б)

R

R

C

Область применения: коррекция автоматических систем с целью снятия самовозбуждения.

Переходные характеристики:

а)

h(t)

t

б)

h(t)

t

К

Вопрос 7

Форсирующее и колебательное звенья, их характеристики

Форсирующее звено является антиинерционным звеном.

.

,

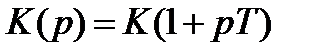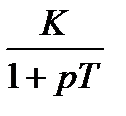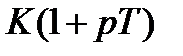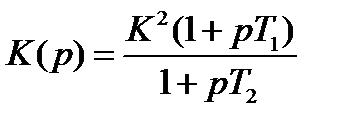T₁ = T₂: K(p) = K².

Физически сделать трудно.

Дифференциальное уравнение:

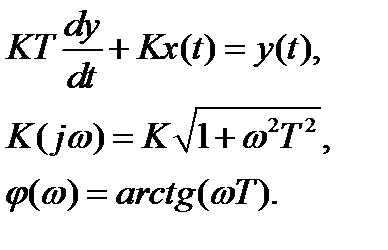
A(ω)

K

ω

φ(ω)

π/2

ω

Im

K

Re

L(ω)

1/T

ω

-20 дБ/дек

.

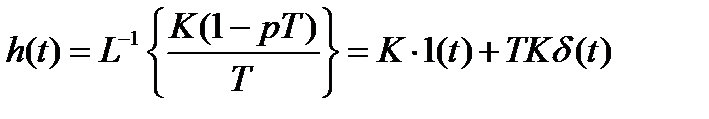h(t)

t

K

R2

C

R1

R2/R1

Область применения: борьба с инерционностью.

Колебательное звено:

.

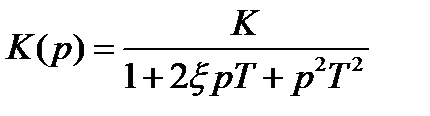ξ – коэффициент затухания (соизмерим с 1).

, .

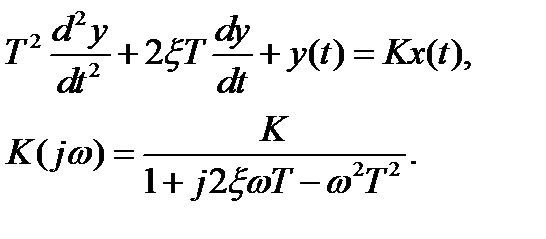
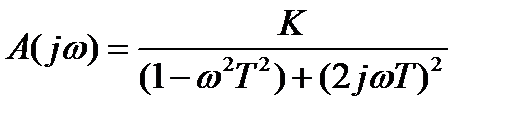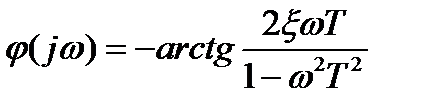1/T

ω

A

ω

φ

-90°

-180°

Re

Im

K

ξ=0.9

t

ξ=0.7

Чем меньше ξ, тем дольше происходят колебания.

R

C

L

Часто встречается в автоматических системах.

Вопрос 8

Передаточные функции разомкнутых и замкнутых систем, передаточные функции ошибки от регулирующего и возмущающего воздействий

Передаточная функция (ПФ) разомкнутых систем:

Рассмотрим следящую систему.

K1(p)

K2(p)

K3(p)

ξ

y

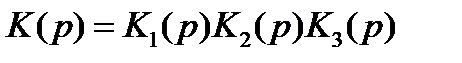
K1(p)

K2(p)

K3(p)

z

y

K4(p)

ξ

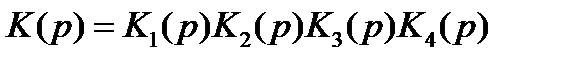- передаточная функция разомкнутой системы. Сигнал z должен копировать сигнал x.

ПФ замкнутой системы

K(p)

ξ

y

x

K(p) включает в себя все 3 звена.

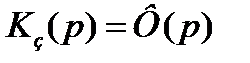- ПФ замкнутой системы.

.

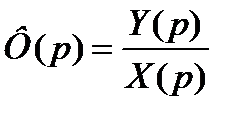Из-за обратной связи

.

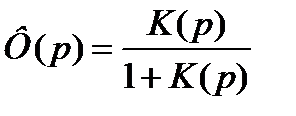Не следящая система

K1(p)

ξ

y

x

K1(p)

z

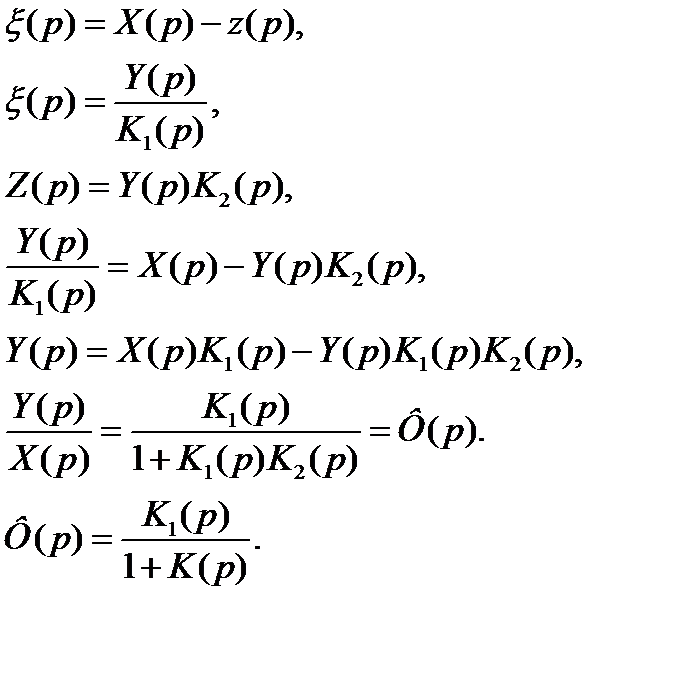
ПФ ошибки от регулирующего воздействия:

K(p)

ξ

y

x

ПФ от регулирующего воздействия одинакова как для следящей, так и для не следящей системы.

ПФ ошибки от возмущающего воздействия:

K1(p)

K2(p)

z

y

K3(p)

ξ

F

F ≠ 0, x ≠ 0.

F – возмущающее воздействие, помеха K_ξF.

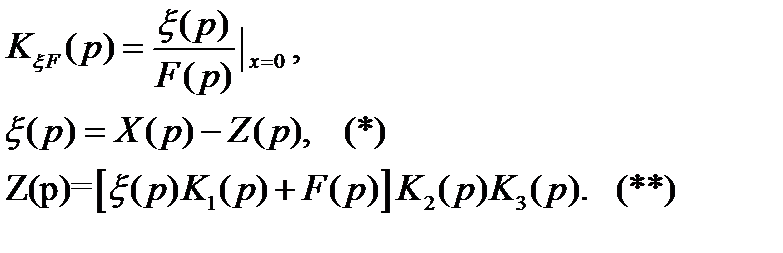
Подставляем (**) в (*) при x = 0:

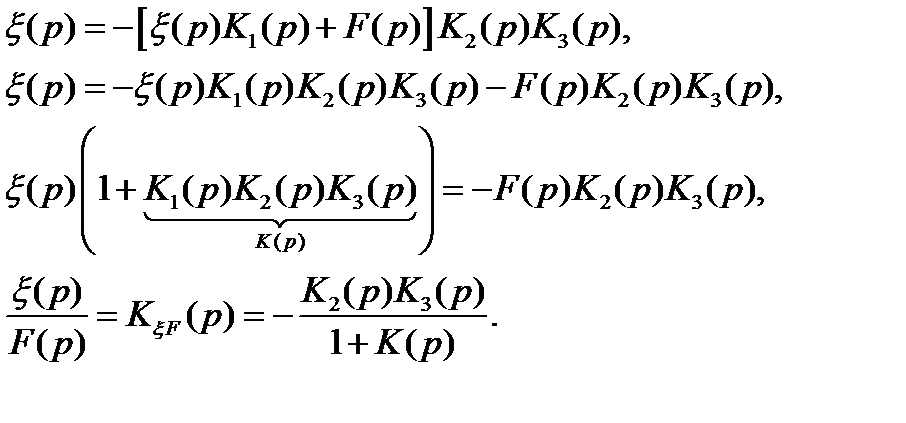
Передаточная функция ошибки возмущающего воздействия есть отношение, где в числителе со знаком минус взята передаточная функция части системы, находящейся между точкой приложения возмущающего воздействия и сумматором (по ходу сигнала).

Поскольку система линейная, соблюдается принцип суперпозиции (независимость прохождения сигналов друг от друга):

.

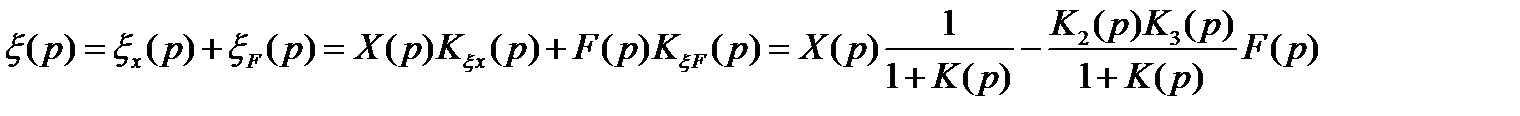Вопрос 9

Устойчивость линейных САУ. Теорема Ляпунова. Критерий Гурвица

Устойчивость – свойство системы возвращаться в условие равновесия после снятия внешних сил, выведших её из состояния равновесия.

t

y

Траектория описывается уравнением

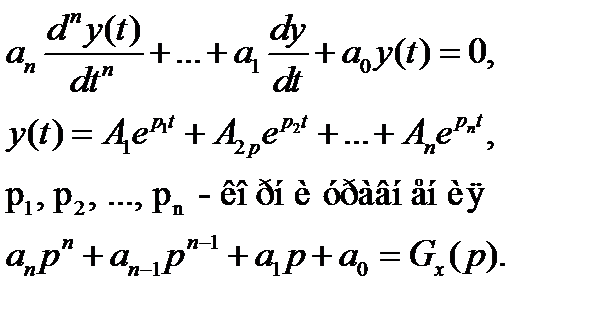
Самыми распространёнными критериями определения устойчивости системы являются алгебраический критерий Гурвица, частотные критерии Найквиста и Михайлова.

Теорема Ляпунова:

Если в характеристическом полиноме системы нет корней с положительными или нулевыми вещественными частями, то такая система будет устойчива.

Критерий Гурвица:

Необходимое условие устойчивости:

Все коэффициенты характеристического полинома системы должны быть положительны:

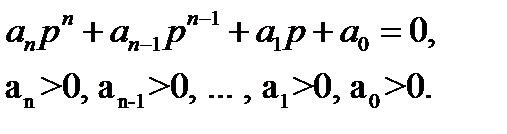
Тогда все корни данного уравнения будут иметь отрицательные вещественные части.

Достаточное условие устойчивости

Все диагональные определители матрицы должны быть положительны.

Матрица размера nx n (n – максимальная степень полинома).

По диагонали сверху вниз вписываются коэффициенты от a_n-1 до a₀, остальные по возрастанию вправо, по убыванию влево, и нули.

Например, если полином 4-й степени, то матрица будет иметь вид:

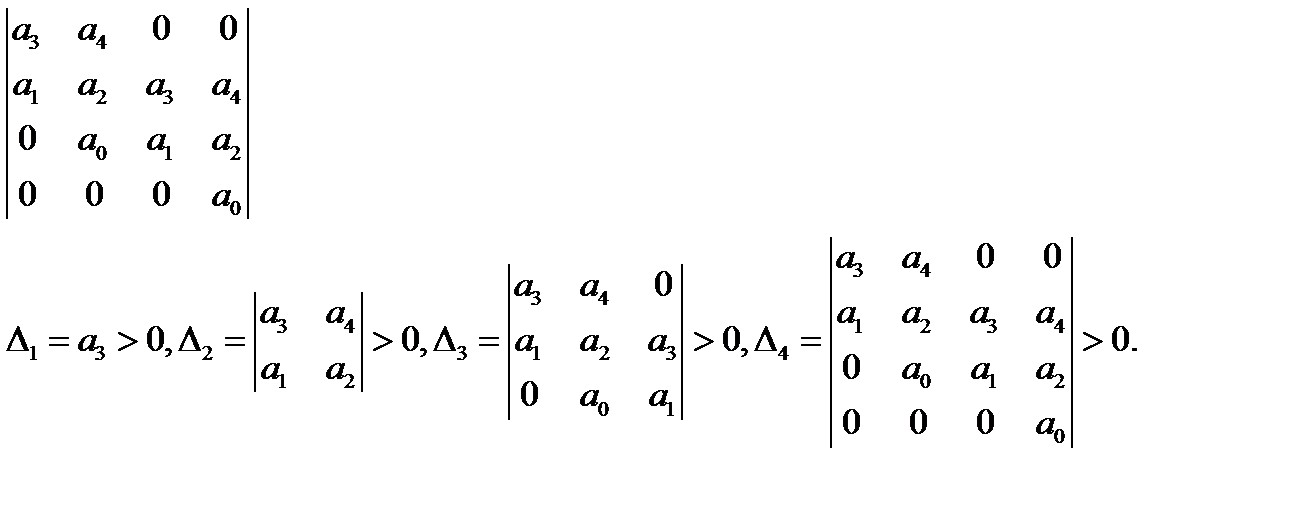
Вопрос 10

Частотный критерий Найквиста. Примеры

Частотный критерия Найквиста позволяет определить, какими параметрами устойчивости обладает данная система.

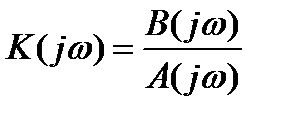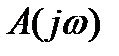, - характеристическая функция разомкнутой системы.

.

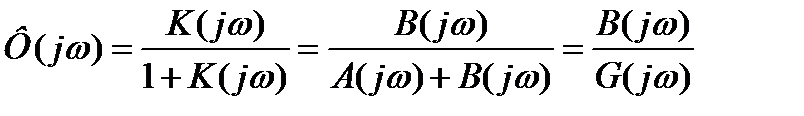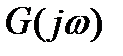- характеристическая частотная функция замкнутой системы.

Передаточная функция ошибки:

Рассмотрим 2 возможные ситуации:

I. Разомкнутая система устойчива. Найдём условие, при котором замкнутая система тоже будет устойчива.

A(p) = 0 – характеристическое уравнение разомкнутой системы.

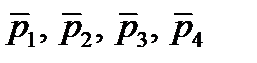- корни.

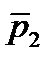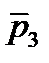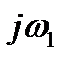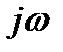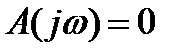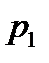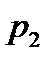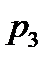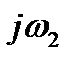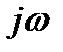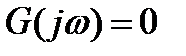корни Михайлова

.

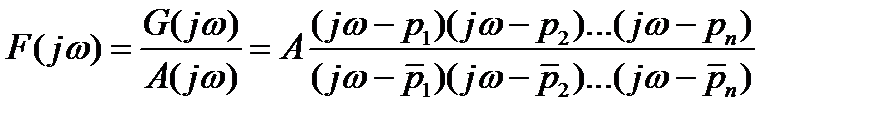Фазовый набег: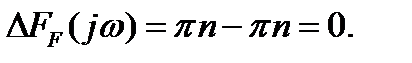

-1

F(jω)=1+ K(jω)

K(jω)

Im

Re

ω1

Если разомкнутая система устойчива, то замкнутая система может быть устойчива, если годограф функции K(jω) разомкнутой системы в диапазоне частот от 0 до ∞ не охватывает точку (-1, 0) на вещественной оси.

Примеры:

Статическая система

K₁ < K₃ < K₂, K₃ – критический коэффициент усиления.

-1

K1K3K2

Im

Re

-1

Im

Re

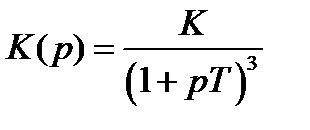. Астатическая система

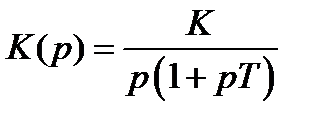- интегрирующее звено сразу даёт сдвиг 90°. Эта система структурно устойчива.

Система структурно не устойчива с двойным интегрирующим звеном:

-1

Im

Re

.

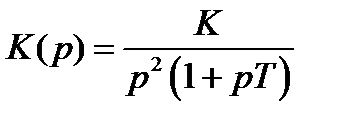Вопрос 11

II. Разомкнутая система неустойчива, а замкнутая система будет устойчивая.

Im

Im

Re

Re

Пусть в уравнении A(p)=0 из n корней m в правой полуплоскости:

Im

Re

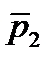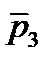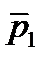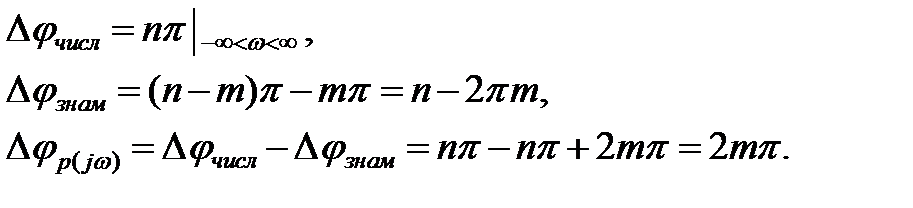
Если разомкнутая система неустойчива и её характеристическое уравнение A(p)=0 имеет m корней с положительной вещественной частью, то для устойчивости замкнутой системы фазовый набег вектора F(jω) должен составлять m/2 полных оборота (годограф K(jω) в диапазоне частот от 0 до ∞ m/2 раз против часовой стрелки охватывает точку (-1,0)).

Пример:

Если m=2, то годограф для устойчивого состояния должен 1 раз охватить точку (-1,0).

-1

Im

Re

устойчивая

-1

Im

Re

устойчивая

-1

Im

Re

неустойчивая

m=3:

-1

Im

Re

устойчивая

-1

Im

Re

устойчивая

-1

Im

Re

неустойчивая

Вопрос 12

Частотный критерий Михайлова. Примеры

t

y

Траектория описывается уравнением

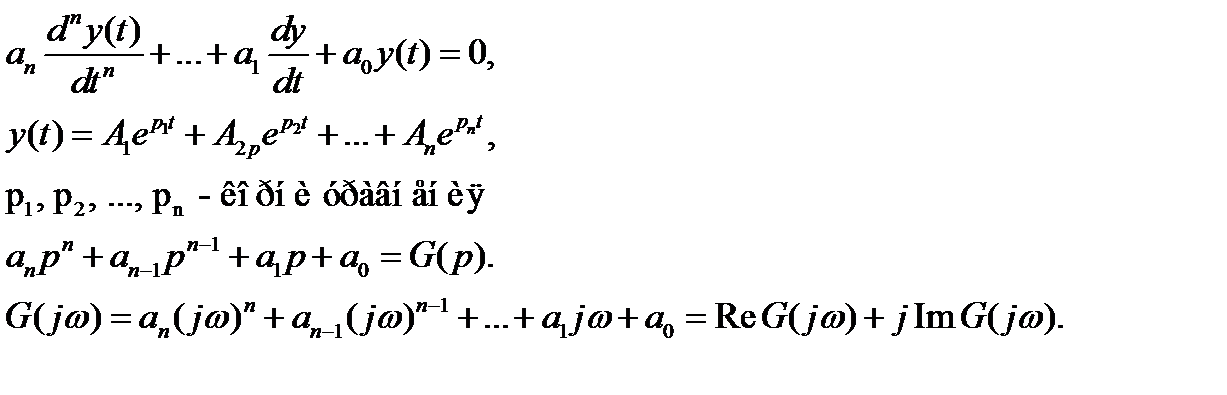
Все корни должны быть в левой полплоскости:

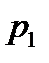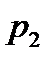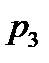jω

α

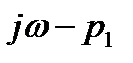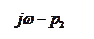
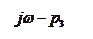
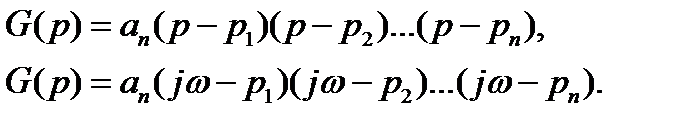
Фазовый набег вектора G(jω):

Im

Re

G(0)

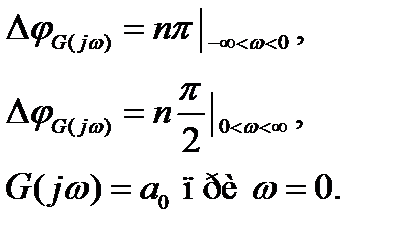
- Годограф характеристической частотной функции замкнутой системы (годограф Михайлова)

Частотный критерий Михайлова:

Замкнутая система будет устойчива, если годограф характеристической частотной функции замкнутой системы при изменении частоты от 0 до ∞, начинаясь с вещественной оси, последовательно, против часовой стрелки, обходит n квадрантов и в последнем квадранте уходит в бесконечность.

Im

Re

неустойчивое состояние

Im

Re

устойчивое состояние

Вопрос 13

Следствием из применения критерия устойчивости Михайлова является правило чередующихся корней: при движении точки по годографу в направлении возрастания частоты годограф должен последовательно пересекать вещественную и мнимую оси, ни разу не пересекая дважды одну и ту же ось.

Пример:

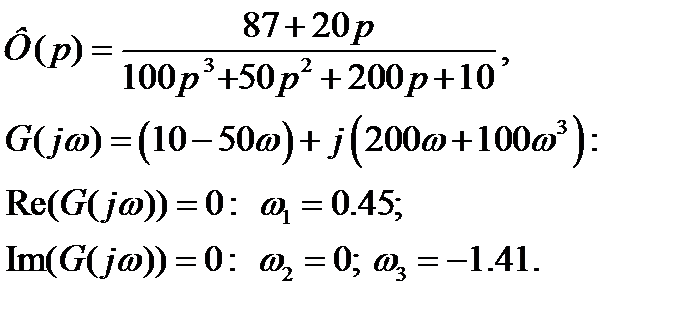
Im

Re

Система устойчива

ω2

ω1

ω3

Вопрос 14

Качество регулирования в установившемся и вынужденном режимах. Примеры

Под качеством регулирования подразумевают величину ошибки регулирования при воздействии на систему детерминированного сигнала.

Чем меньше ошибка, тем выше качество.

K(p)

ξ

y

x

Ошибка ξ(p): ξ(p) = X(p) – Y(p).

Выделение ошибки – функция сумматора.

Определить ошибку можно несколькими способами:

1. а) записать ДУ замкнутой системы;

б) подставить в это уравнение ожидаемое решение в виде какой-то функции с неизвестными коэффициентами;

в) определить эти коэффициенты;

2. Классический операторный метод

а) найти изображение по Лапласу известной функции x(t);

б) по известной структуре системы K(p) находим передаточную функцию ошибки K_ξx(p):

;

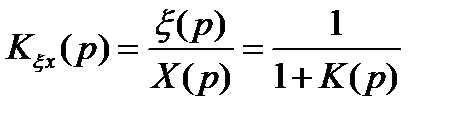в) обратным преобразованием Лапласа определяем ξ(t) по таблицам.

3. Метод коэффициентов ошибки

а) раскладываем передаточную функцию K_ξx(p) в ряд по степеням комплексной переменной p;

б) записываем ДУ в операторной форме:

,

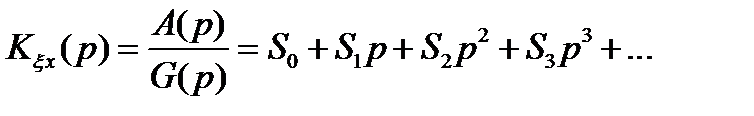где S₀,…S_n – коэффициенты ошибки.

в) переходим от операторной к классической форме:

;

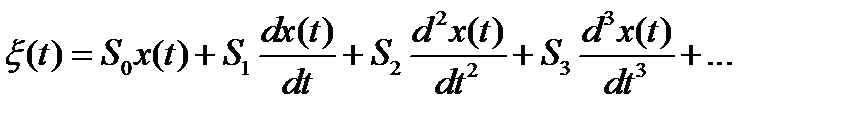г) находим коэффициенты через известные коэффициенты полиномов G(p) и A(p).

Выводы:

1. Ошибка регулирования зависит от формы управляющего сигнала и от порядка астатизма системы;

2. Чем динамичнее входной сигнал, тем больший порядок астатизма требуется для приближения к нулевой ошибке;

3. Для нулевой ошибки необходим порядок астатизма на единицу больше числа ненулевых производных входного сигнала;

4. Если порядок астатизма равен числу ненулевых производных, ошибка постоянна;

5. Если порядок астатизма меньше, чем число ненулевых производных, ошибка регулирования будет возрастать со временем;

6. Чем больше коэффициент усиления, тем меньше ошибка.

Вопрос 15

Связь между структурой системы, входным воздействием и ошибкой регулирования. Примеры

Ошибка регулирования зависит от формы регулирующего воздействия и порядка астатизма системы. Порядок астатизма определяется количеством интегрирующих звеньев.

Рассмотрим метод коэффициентов ошибки.

Пример:

На входе приложено постоянное воздействие x(t) = A.

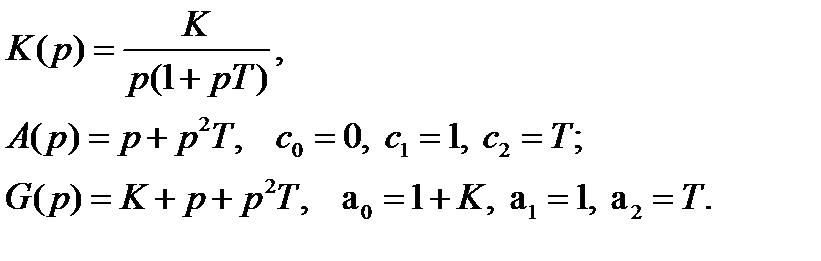
Так как в знаменателе нет свободного члена (из-за наличия интегрирующего звена), то c₀ =0, значит коэффициент S₀ = 0, остальные S_i не равны 0.

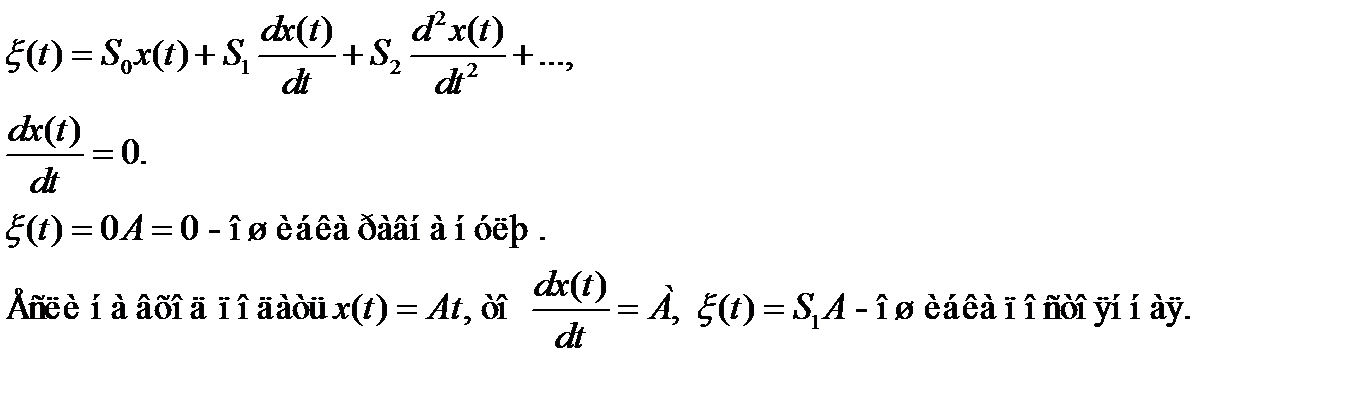
Отсюда мы можем сделать вывод, что для получения нулевой ошибки регулирования порядок астатизма должен быть на единицу больше числа ненулевых производных входного сигнала x(t); если же они равны, то ошибка будет постоянной; если порядок астатизма больше числа ненулевых производных x(t), то ошибка будет расти.

Самыми мощными являются первые компоненты, поэтому есть смысл использовать астатические системы даже при очень динамических входных сигналах.

Вопрос 16????????

Качество переходных режимов, методы определения параметров качества

Δh

T

tр

tс

hуст

hm

h

t

t_р – время достижения максимального выброса, t_c – время завершения переходного процесса, h_m – максимальное значение переходной характеристики.

.

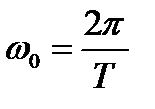- частота колебания на вершине переходного процесса.

Переходные процессы важнее там, где система должна быть быстродействующей.

Способы определения качества переходных процессов

1. Аналитический способ

В его основе лежит передаточная функция системы и знание теории цепей:

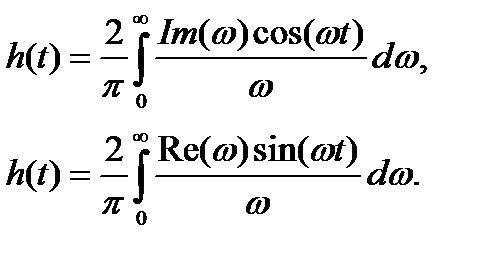
2. Графический способ(по ЛАЧХ).