Примеры программной реализации
РЕГУЛЯТОРА СКОРОСТИ И МОДЕЛИРОВАНИЯ
КОНТУРА СКОРОСТИ
Пример 4.1 (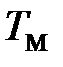 
< 
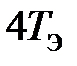).Провести дискретную аппроксимацию передаточной функции регулятора скорости и получить векторно-матричные уравнения цифрового регулятора. Для расчёта использовать данные, рассчитанные в примере 2.2б. Принять период квантования Т0 = 0,001 с.
Решение.Поскольку, 4Тэ больше, чем Тм, то передаточную функцию регулятора скорости представим в виде
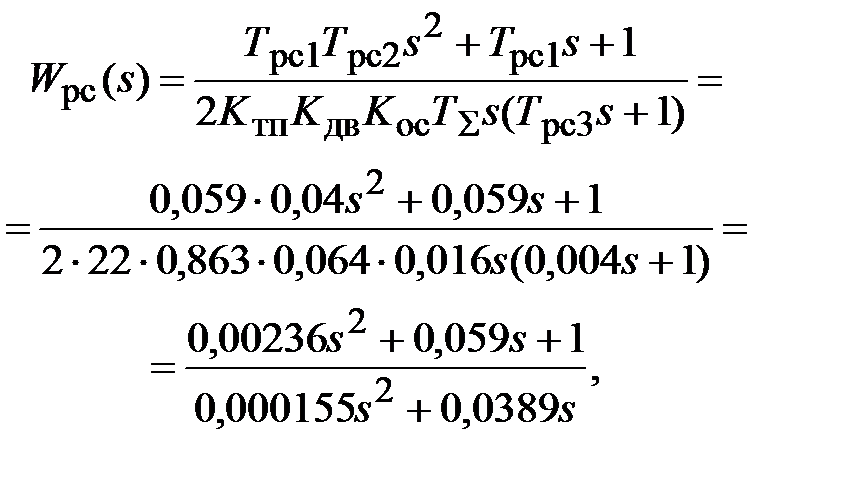
где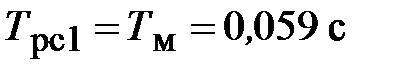 
, 
, 
, 
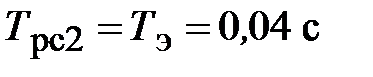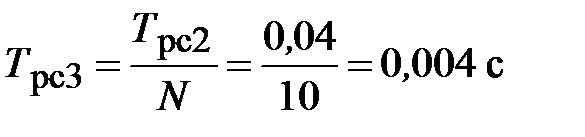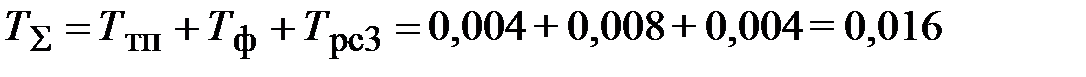с.
Для определения передаточной функции цифрового регулятора скорости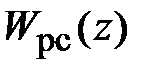 
с применением формулы трапеций (4.3) составим программу:
num=[0.00236 0.059 1];
den=[0.000155 0.0389 0];
fs=1000;
[numd, dend]=bilinear(num, den, fs)
numd =
13.6988 -27.0536 13.3606
dend =
1.0000 -1.7770 0.7770
В приведенной программе частота дискретизации
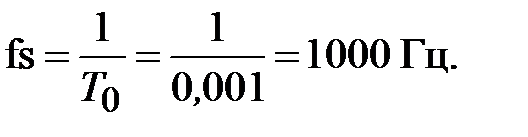
В результате выполнения программы получаем передаточную функцию цифрового регулятора скорости
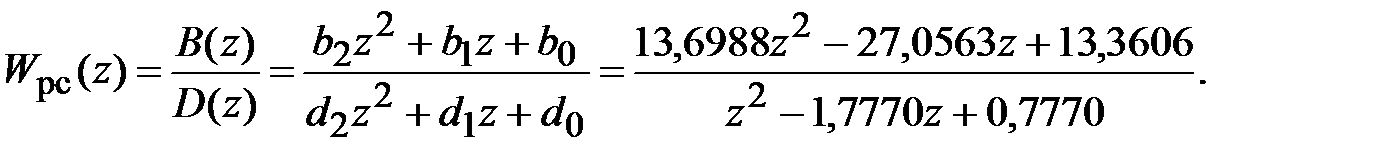
Для получения уравнений состояния цифрового регулятора скорости применим метод непосредственного программирования. Структурная схема представлена на рис. 4.6.
Рис. 4.6. Структурная схема непосредственного программирования
По схеме программирования находим уравнения состояния и выхода системы[1].
Уравнения состояния:
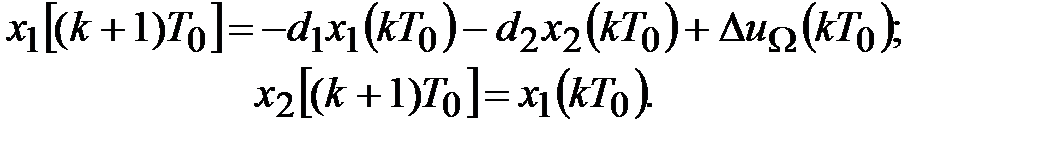
Уравнение выхода
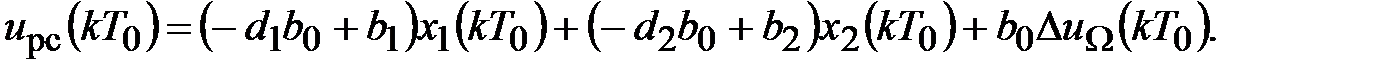
Векторно-матричная форма уравнений цифрового регулятора скорости:
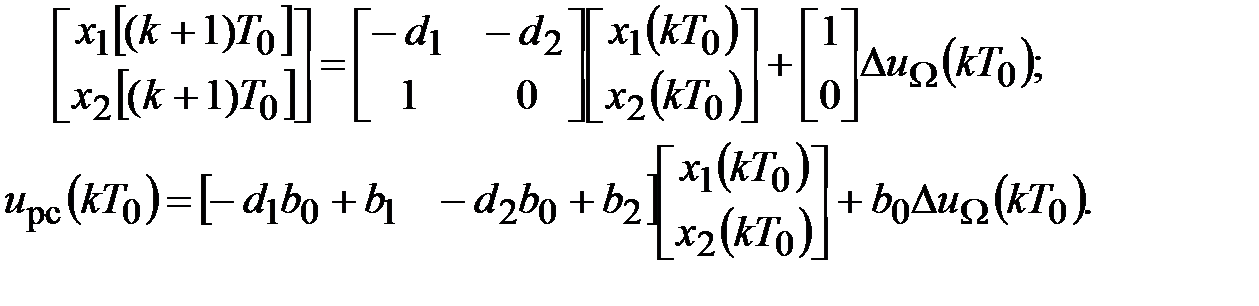
Коэффициенты матриц векторно-матричной формы записи уравнений цифрового регулятора скорости получим с применением программы:
num=[13.6988 -27.0536 13.3606];
den=[1.0000 -1.7770 0.7770];
[A, B, C, D]=tf2ss(num, den)
A =
1.7770 -0.7770
1.0000 0
B =
C =
-2.7108 2.7166
D =
13.6988
; 
; 
; 
.
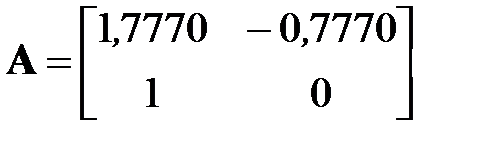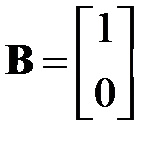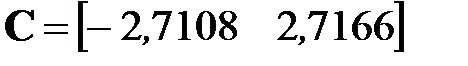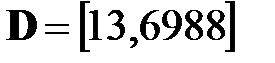Пример 4.2.Составить ССДМ КС с цифровым регулятором скорости. Получить графики зависимостей угловой скорости по сигналу задания и моменту сопротивления. Построить логарифмические псевдочастотные характеристики (ЛПЧХ). Провести анализ результатов моделирования. Записать рабочую программу цифрового регулятора скорости в среде программирования CoDeSys. Коэффициент передачи АЦП Кvz2 = 1.
Решение.Для моделирования построим ССДМ КС с цифровым регулятором скорости в системе Simulink (рис. 4.7).
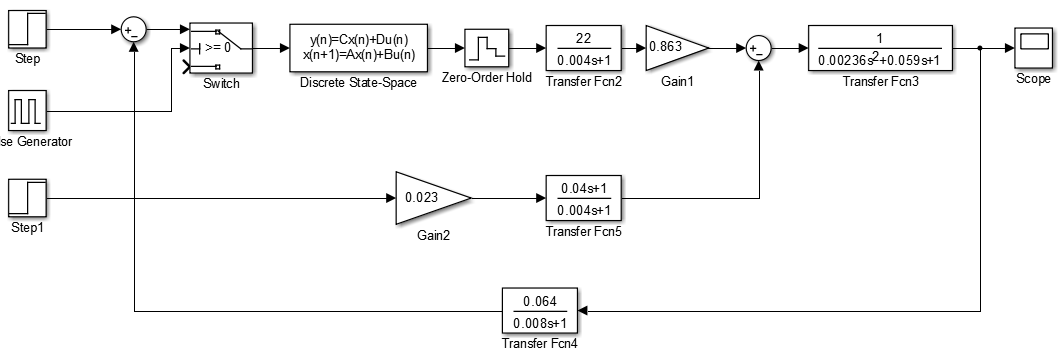
Рис. 4.7. Структурная схема динамической модели контура скорости
с цифровым регулятором скорости
Цифровой регулятор скорости реализован блоком Discrete State-Space, расположенным в библиотеке блоков Discrete. Диалоговое окно блока представлено на рис. 4.8.
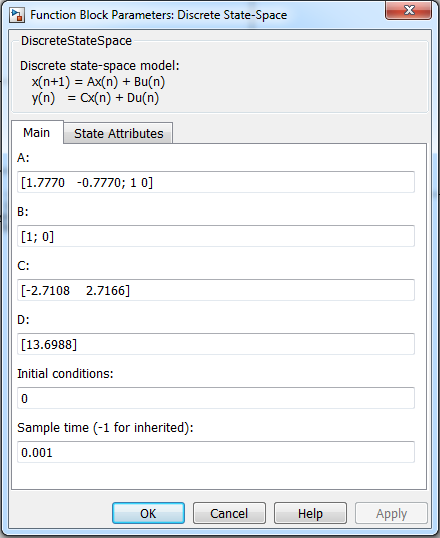
Рис. 4.8. Диалоговое окно блока Discrete State-Space
Блок Zero-Order Hold представляет собой экстраполятор нулевого порядка, восстанавливающий непрерывный сигнал uрс с выхода цифрового регулятора скорости. Блок Switch реализует модель квантователя, преобразующего непрерывный сигнал рассогласования∆uΩ в дискретный. Блок Pulse Generator формирует последовательность единичных импульсов с периодом следования Т0.
Для задания параметров блока Zero-Order Hold необходимо в строке Sample time установить период квантования Т0 (рис. 4.9).
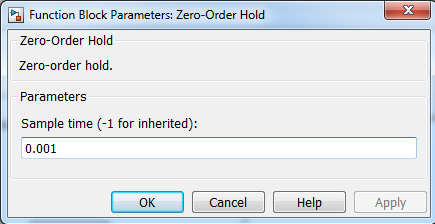
Рис. 4.9. Диалоговое окно блока Zero-Order Hold
Для задания параметров блока Pulse Generator необходимо в строке Period установить период квантования Т0 (рис. 4.10).
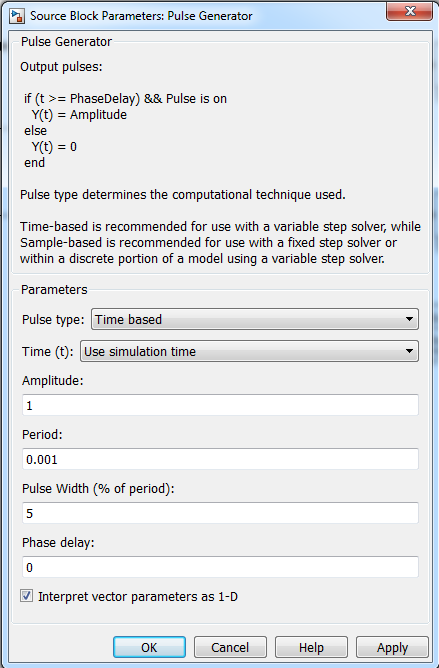
Рис. 4.10. Диалоговое окно блока Pulse Generator
Для получения графика в блоке Step задаём входное воздействие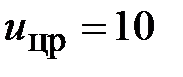 
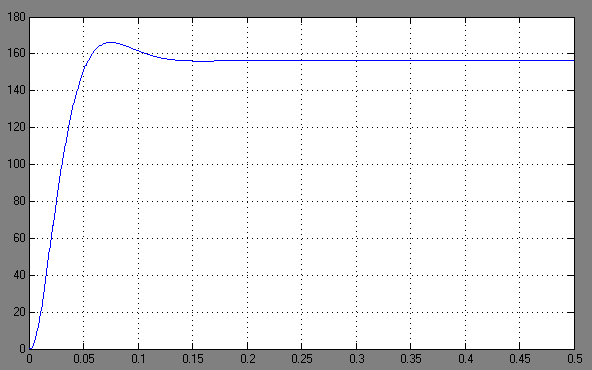
В, а в блоке Step1 значение момента сопротивления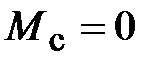 
. На рис. 4.11 изображена зависимость скорости вращения скорректированного контура скорости по сигналу задания. Время моделирования составляет 0,5 с.
Ω(t), рад/с
t, c
Рис. 4.11. График зависимости угловой скорости от времени скорректированного контура скорости по сигналу задания
Ω(t), рад/с
t, c
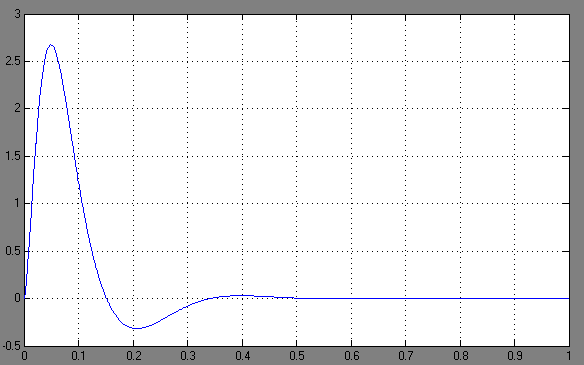
Рис. 4.12. График зависимости угловой скорости от времени скорректированного контура скорости по моменту
сопротивления
Для построения графика зависимости угловой скорости от времени скорректированного контура скорости по моменту сопротивления нагрузки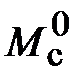 
устанавливаем в блоке Step входное воздействие 
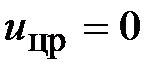, а в блоке Step 1 момент сопротивления 
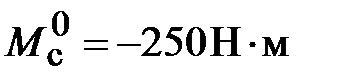. Результаты моделирования представлены на рис. 4.12.
Переходим к анализу полученных графиков. По характеристике на рис. 4.11 определяем максимальное значение угловой скорости вращения ЭД Ωmax = 166 рад/с и установившееся значение Ωуст = 157 рад/с. По этим данным рассчитываем перерегулирование
.
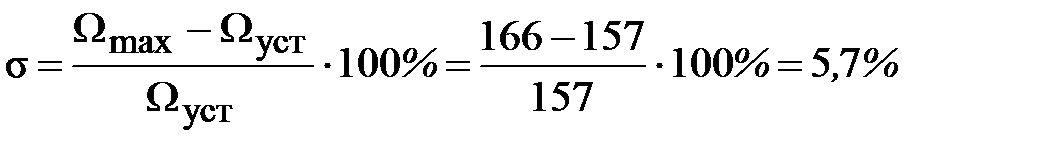Время нарастания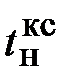 
составляет
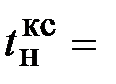0,055 с.
Проверяем соответствия требованиям настройки на ОМ
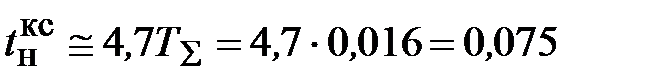с.
Из анализа графика на рис. 4.12 следует, что при воздействии неизменного по величине момента сопротивления 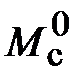моментная составляющая ошибки ΔΩм примерно через 0,5 с становится равной нулю. Это говорит о том, что искусственная механическая характеристика стала абсолютно жёсткой. Увеличение точности обусловлено наличием в структуре регулятора скорости интегральной составляющей.
Для построения ЛПЧХ определим передаточную функцию разомкнутого контура скорости Wкс(s) в соответствии с программой:
num1=[0.00236 0.059 1];
den1=[0.000155 0.0389 0];
sys1=tf(num1, den1);
num2=[22];
den2=[0.004 1];
sys2=tf(num2, den2);
num3=[0.863];
den3=[0.00236 0.059 1];
sys3=tf(num3, den3);
num4=[0.064];
den4=[0.008 1];
sys4=tf(num4, den4);
sys5=sys1*sys2*sys3*sys4
sys5 =
0.002868 s^2 + 0.07169 s + 1.215
--------------------------------------------------------------------------------------
1.171e-11 s^6 + 7.62e-09 s^5 + 1.656e-06 s^4 + 0.0001316 s^3 + +0.002917 s^2 + 0.0389 s
Переходим к переменной z и определяем передаточную функцию разомкнутого контура скорости Wкс(z):
num=[0.002868 0.07169 1.215];
den=[1.171e-11 7.62e-09 1.656e-06 0.0001316 0.002917 0.0389 0];
fs=1000;
[numd, dend]=bilinear(num, den, fs)
numd =
1.0e-04 *
0.113794412337498 0.230445490219111 -0.105176807885243
-0.449273886999890 -0.119222096426341 0.219209259388897 0.110985354633275
dend =
1.000000000000000 -5.412175658119320 12.177351665884430
-14.579027775916543 9.794918887321495 -3.501280381059882 0.520213261889818
Ниже приведена программа построения ЛПЧХ с использованием υ-преобразования (4.9) в форме
.
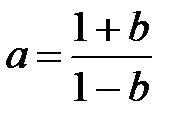syms a b;
a=(1+b)/(1-b);
simplify(((0.113794412337498*a^6+0.230445490219111*a^5-0.105176807885243*a^4-0.449273886999890*a^3-0.119222096426341*a^2+0.219209259388897*a+0.110985354633275)*1.0e-04)/(1.000000000000000*a^6-5.412175658119320*a^5+12.177351665884430*a^4-14.579027775916543*a^3+9.794918887321495*a^2-3.501280381059882*a+0.520213261889818))
ans =
(1840027*b^6 - 479978*b^5 - 5999915*b^4 - 2879852*b^3 + +259125983100239917*b^2 + 3238623038240070*b + +27444045040019)/(40000*(423202965422690413*b^6 + +137694560056400434*b^5 + 14962086053372643*b^4 + +594508008642556*b^3 + 6588829259875*b^2 + 43933057586*b - 19))
По полученной дискретной передаточной функции разомкнутого контура скорости
переходим к построению ЛПЧХ в соответствии с программой:
num=[1840027 -479978 -5999915 -2879852 259125983100239917 3238623038240070 27444045040019];
den=[40000*423202965422690413 40000*137694560056400434 40000*14962086053372643 40000*594508008642556 40000*6588829259875 40000*43933057586 -40000*19];
bode(num, den)
Результаты моделирования представлены на рис. 4.13.
Рис. 4.13. Логарифмические псевдочастотные характеристики
В передаточной функции разомкнутого контура скорости Wкс(b), полученной в результате υ-преобразования в числителе и знаменателе имеются коэффициенты с отрицательными знаками. Поскольку после υ-преобразования дискретную систему можно рассматривать как линейную непрерывную, то, в соответствии с критерием Гурвица, можно сделать вывод о том, что она является неминимально-фазовой, т.е., имеет положительные нули и полюсы.
У таких систем ЛАЧХ не отличается от ЛАЧХ минимально фазовых систем, поскольку модуль комплексного числа не зависит от знака действительной или мнимой части. При этом график в полярных координатах не изменится в результате поворота на 360° или –360°. ЛФЧХ на рис. 4.13 смещена вверх на 360° по сравнению с ЛФЧХ минимально-фазового контура скорости Wкс(s) (рис. 3.12).
Рассмотрим более наглядно определение запасов устойчивости с помощью амплитудно-фазовой частотной характеристики (АФЧХ) с применением программы:
num=[1840027 -479978 -5999915 -2879852 259125983100239917 3238623038240070 27444045040019];
den=[40000*423202965422690413 40000*137694560056400434 40000*14962086053372643 40000*594508008642556 40000*6588829259875 40000*43933057586 -40000*19];
nyquist(num, den)
Результаты моделирования представлены на рис. 4.14.
Запас устойчивости по фазе определяется на частоте среза wс, которая соответствует точке пересечения АФЧХ c окружностью единичного радиуса. Запас устойчивости больше нуля и определяется по формуле
.
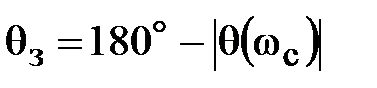В нашем примере wс = 0,015 рад/с (At frequency) (см. рис. 4.14), а запас устойчивости по фазе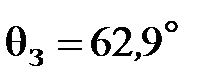 
(Phase Margin).
Запас устойчивости по амплитуде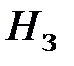 
определяется на отрицательной вещественной полуоси как соотношение
,
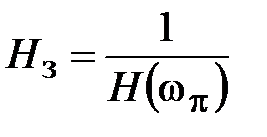где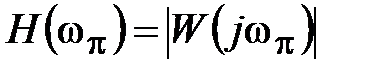 
.
Рис. 4.14. Амплитудно-фазовая псевдочастотная характеристика
Частота wπ соответствует значению аргумента вектора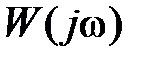 
, равного 
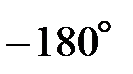. В логарифмическом масштабе запас устойчивости по амплитуде запишется в виде
.
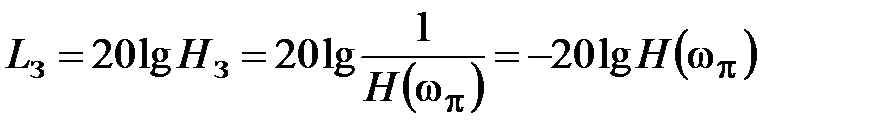Поскольку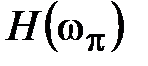 
меньше единицы, то запас устойчивости по амплитуде всегда больше нуля. В нашем случае wπ = 0,056 рад/с, 
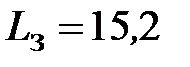дБ (см. рис. 4.16).
Необходимо отметить, что графики псевдочастотных характеристик смещаются на величину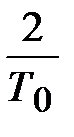 
, при этом запасы устойчивости по фазе и амплитуде останутся прежними.
Алгоритм работы цифрового регулятора скорости в виде полученных разностных уравнений реализуем на промышленном контроллере типа ПЛК154 производства компании Овен с помощью программы в среде CoDeSys, которая позволяет составить, проверить и отладить программу в режиме симуляции без загрузки в цифровой регулятор (контроллер). Ниже приведен листинг программы, реализующей цифровой регулятор положения и окно редактирования в среде программирования CoDeSys (рис. 4.15). Редактор состоит из раздела объявлений (верхняя часть) и раздела кода (нижняя часть).
PROGRAM PLC_PRG
VAR_INPUT
in:REAL;
END_VAR
VAR_OUTPUT
out:REAL;
END_VAR
VAR
x1: REAL:=0; x2: REAL:=0; x12: REAL:=0;
x22: REAL:=0; Urs: REAL:=0; dU:REAL:=0;
END_VAR
Считывание сигнала рассогласования с входа контроллера
dU:=in;
Вычисление уравнений состояния
x1:=1.7770*x12-0.7770*x22+dU;
x2:=x12;
Вычисление уравнения выхода
Urs:=-2.7108*x12+2.7166*x22+13.6988*dU;
Запись сигнала управления на выход контроллера
out:=Urs;
x12:=x1;
x22:=x2;
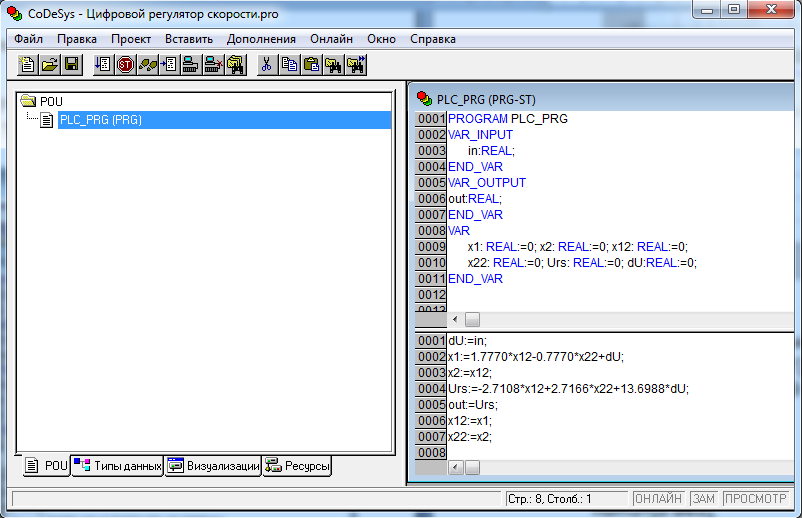
Рис. 4.15. Рабочая программа цифрового регулятора скорости
в среде CoDeSys
В начале программы, приведенной на рис. 4.15 описываются используемые переменные и их тип (REAL – переменная с плавающей запятой), затем следует сама программа, где описываются все вычисления.
Расчет начинается со считывания значения сигнала рассогласования с входа регулятора (функция dU:=in). Затем производится расчет новых значений уравнений состояния и выхода. Полученное значение выходного сигнала (Urs) подается на аналоговый выход регулятора (функция out:=Urs) для дальнейшего использования в системе управления. Программа работает в циклическом режиме и постоянно отслеживает состояние системы, сводя к минимуму значение сигнала рассогласования.
Проверка рабочей программы цифрового регулятора скорости проведена с помощью моделирования, результаты которого представлены на рис. 4.16.
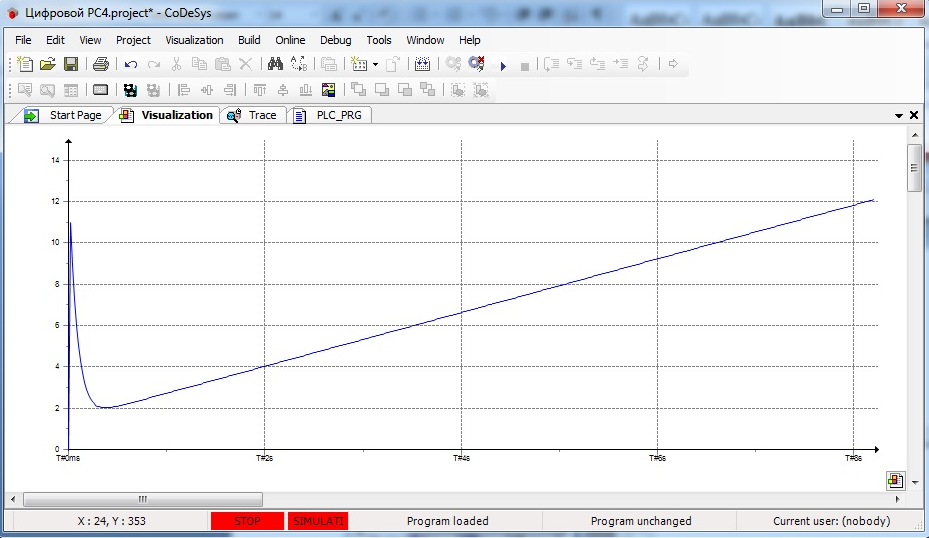
Рис. 4.16. Переходная характеристика цифрового регулятора скорости
в среде CoDeSys
Реакция цифрового регулятора скорости на единичный скачок представляет собой сумму дельта-функции Дирака, полученной при дифференцировании единичного скачка в момент времени t = 0 (нуль, близкий к окружности единичного радиуса), постоянной составляющей и прямой линии, соответствующей операции интегрирования (полюс на окружности единичного радиуса). Полученные результаты подтверждают правильность синтеза ПИД-регулятора
Отчётные материалы
1. Структурная схема непосредственного программирования цифрового регулятора скорости.
2. Векторно-матричные уравнения цифрового регулятора скорости.
3. Структурная схема динамической модели контура скорости с цифровым регулятором скорости.
4. Графики зависимостей угловой скорости от времени скорректированного контура скорости сигналу задания и моменту сопротивления и их анализ.
5. Z-преобразование и υ-преобразование передаточной функции разомкнутого контура скорости с применением MatLab.
6. Логарифмические псевдочастотные характеристики и их анализ.
7. Рабочая программа цифрового регулятора скорости в среде CoDeSys.
Контрольные вопросы
1. Записать и пояснить уравнения состояния непрерывных систем управления.
2. Записать и пояснить уравнения состояния цифровых систем управления.
3. Изобразить векторную структурную схему динамической модели системы в переменных состояния.
4. Объяснить метод непосредственного программирования цифровых регуляторов.
5. Объяснить метод последовательного программирования цифровых регуляторов.
6. Объяснить метод параллельного программирования цифровых регуляторов.
7. Показать методику получения векторно-матричных уравнений состояния цифровых регуляторов.
8. Пояснить частотные методы анализа и синтеза применительно к цифровым системам управления.
9. Изложить порядок исследования цифровых систем управления в системе Simulink.
10. Объяснить результаты моделирования цифровых систем управления во временной и частотной областях в системе MatLab.
ЛАБОРАТОРНАЯ РАБОТА № 5