Дополнительные проблемы с измерением и материалами

Возможная экономия при сборке изделия из блоков. Согласно вышеизложенной теории, издержки К₂ быстро вырастают (возможно, 10-кратно), на каждой стадии производственного цикла и достигают значительной величины на стадии окончательной сборки. Иногда оказывается возможным избежать высоких затрат путем конструирования промежуточных блоков, которые идут на сборку конечного изделия. Эти несколько промежуточных блоков, пройдя проверку, регулировку и замены, которые окажутся необходимыми, станут новой точкой отсчета. Издержки к₂ согласно вышеизложенной теория, образуют стоимость проверки и регулировки промежуточного блока. Эта теория в совокупности с соответствующим опытом может указать, что некоторые промежуточные блоки вообще не нуждаются в проверке, в то время как другие должны быть подвергнуты 100%-му контролю качества во избежание более высоких затрат на последующих стадиях. Теория, изложенная в этой главе, обеспечивает руководство в решении проблем качества. Выше мы просто пытались показать, что всегда существуют возможности снизить издержки до минимума и добиться максимальной прибыли, руководствуясь подходящей теорией.

Тем временем мы прилагаем все усилия к тому, чтобы полностью устранить все дефектные изделия. Мы это делаем систематически, сравнивая наши результаты с тестами поставщика, а также используя соответствующие статистические приемы, такие как х и Р - диаграммы.

Успешное сотрудничество с поставщиком комплектующих деталей, особенно критических, а также успешное тестирование и доводка промежуточных блоков, снижают до минимального уровня любые серьезные трудности на стадии контроля качества конечного изделия.

Трудности в обнаружении исключительно редких дефектов. Редкие дефекты обнаружить трудно. По мере уменьшения доли дефектной продукция, растет и сложность обнаружения того, насколько она мала. Контроль качества просто не обнаруживает все дефектные изделия, особенно если они редки. Независимо от того, осуществляется ли контроль визуально или механически. Не имеет особого смысла принимать на веру заявление одного изготовителя о том, что он производит только одно бракованное изделие на 10 тысяч, сравнительно с другим, который уверяет, что у него только одно бракованное изделие на 5 тысяч. В любом случае истинную пропорцию установить затруднительно.

Таким образом, если р=I/5000 и если процесс находится в рамках статистической нормы, необходимо обследовать 80000 деталей, чтобы обнаружить 16 дефектных. Эта цифра р=I/5000 для процесса производства, со стандартной ошибкой - или 25%. Таким образом, точность оценки доли дефектной продукции не слишком высока, несмотря на изрядный объем проверки: 80000 деталей. Можно задать вопрос, оставался ли производственный процесс стабильным на протяжении изготовления этих 80000 деталей. Был ля он одинаков в начале и в конце их изготовления? Если нет, каков смысл упоминания о 16 дефектны изделиях? Сложный вопрос.

Существуют примеры безотказной работы миллионов деталей, даже почти или полностью безотказной работы миллиарда деталей. Никакой объем контроля качества готового продукта не способен дать адекватную информацию, когда доля дефектных изделий так мала. Единственно возможный способ узнать ситуацию в условиях экстремальных требований - это использовать диаграммы реальных замеров деталей в процессе изготовления. Сотня наблюдений над 4-мя последовательными изделиями 25 раз в день дадут 25 точек выборки по 4 для Х и Р- диаграмм. Эти диаграммы покажут нам, продолжается ли процесс без изменений или же, что произошел сбой и что выпуск продукта должен быть приостановлен до выяснения причины сбоя. Как только причина сбоя обнаружена, необходимо принять обоснованное решение относительно того, следует ли забраковать всю партию или только часть ее. Взаимодополняющий эффект Х и Р-диаграмм станет немедленно очевиден.

Использование избыточности. При конструировании сложного аппарата может оказаться целесообразным включить в его конструкцию две или более параллельных деталей, с тем, чтобы если одна из них выйдет из строя, другая автоматически заняла бы ее место. Две параллельно работающие детали, для каждой из которых доля брака равна рi, эквивалентны одной, для которой эта величина равна рi². Если например, рi= 1/1000, то рi² =1/1 000 000. Разумеется, ограничения на размер и вес могут исключить использование избыточности. Существуют также другие проблемы: заработает ли в нужный момент дополнительная деталь? Лучшим решением может оказаться высокий уровень надежности одной единственной детали.

Математическая теория ошибок и теория избыточности представляют собой исключительно интересные и важные статистические методы, однако, в данном случае мы вынуждены ограничить обсуждение предмета только этой констатацией.

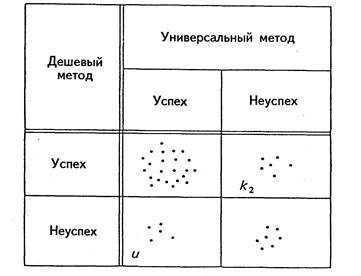
Рис. 48. Таблица 2Х2 для проверки изделий путем использования двух методов. две проверки дают точку в одной из четырех клеточек.

Будет ли более дешевый метод контроля качества более дешевым на практике? Вечный вопрос: как снизить издержки контроля качества, если он необходим (как в Случае 2). Допустим, что существует совершенный метод контроля качества и более дешевый в пересчете на единицу продукции (меньше к₁ метод). Дешевле ли окажется дешевый метод, если мы примем во внимание совокупные издержки? Можно ли в случае неразрушающего тестирования, подвергнуть 200 изделий проверке обоими методами и сообщить результаты в виде таблицы 2Х2, как на рис. 48. Каждая точка представляет результат двух тестов одного изделия. Точка на диагонали означает идентичность результатов обоих тестов. Точка вне диагонали имеет противоположный смысл. деталь, отвергнутая совершенным методом, но пропущенная дешевым (ложное одобрение) явится причиной отказа сложного изделия, издержки на который составят к₂. С другой стороны, деталь, пропущенная при использовании совершенного метода и отвергнутая при применении дешевого (ложное отрицание), вызовет издержки, равные u, то есть стоимости одной детали.

Несложно дать численное представление результатов, использованных в таблице 2Х2. Представим следующую выкладку:

соответственно цифрам в каждой из 4 клеточек. Пусть М будет стоимостью измерения 200 деталей совершенным методом, а С - стоимость использования дешевого метода.

В таком случае, экономия от использования дешевого метода составит:

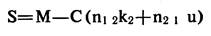
Величины вне диагонали не велики и потому подвержены значительному статистическому разбросу. Стандартная ошибка для величин в клеточках вне диагонали будет с большой степенью приближения равна квадратному корню от этой величины. Таким образом, если величина равна 16, то она будет подвержена стандартной ошибке, равной 4.

Если эта величина равна 9, ее стандартная ошибка будет равна 3. (Эти утверждения основаны на распределении отклонений Пуассона).

Коль скоро представляется сомнительным, что дешевый метод действительно дешевле совершенного, ради большей точности можно протестировать еще 200 и даже 400 деталей. Если сомнения сохранятся, я бы посоветовал остановиться на совершенном методе.

Множественные комплектующие. Только что изложенные рекомендации и вычисления применимы к случаю с одной комплектующей. Допустим, что блок состоит из двух или более комплектующих деталей и что мы хотим применить дешевый метод проверки каждой комплектующей. Собственно говоря, мы можем применить эти вычисления к любой комплектующей и принять соответствующее решение независимо от их количества.

Однако, здесь необходима осторожность. Тестирование дешевым методом любой комплектующей потребует отбора сложных блоков для этой цели. Этот отбор основан на ложном одобрении, представленным правым верхним квадратом рис. 48. Часть выборки для любой комплектующей может совпасть с выборками для других комплектующих, но так как количество комплектующих увеличивается, растет и пропорция тестируемых блоков. Таким образом, при наличии 20 комплектующих деталей и при том, что каждая деталь проверяется дешевым методом, который дает скажем, одно ложное одобрение на 20 случаев, доля блоков, подвергнутых тестированию из-за ложного одобрения будет равна 1‑ (1‑0,05)²⁰= 1‑0,36=0,64.

Если блок состоит из серийных деталей, может возникнуть Необходимость проверить все детали после одного отказа блока.

Отсюда следует мораль, что тестирование может причинить большую неприятность, чем сам продукт. Значительная часть промышленных изделий отвергается на ложном основании только из-за процессов измерения, дающих не согласующиеся друг с другом результаты.

Во избежание ошибочных результатов сравнения, использование как совершенного метода, так и дешевого, должно быть стабильным и находиться в рамках статистической нормы.

Усовершенствованная таблица 2Х2 для получения более точной информации: сравнение работы двух контролеров. 50 деталей поочередно предъявлены двум контролерам, контролеру, 1 и контролеру 2 с целью определить, выдают ли они принципиально одинаковые результаты. Сертификация является защитой, как потребителя, так и производителя. Каждый контролер классифицирует изделия как относящиеся к высшему сорту, или более низкому. Результаты 50 тестов заносятся в две колонки по 50 строчек в порядке прохождения теста; одна колонка для контролера 1 и вторая для контролера 2.

Вместо того, чтобы ставить точку для каждой пары тестов, как на рис. 48, можно добиться более высокой информативности тестирования, указывая не точку, а порядковый номер изделия по ходу тестирования в соответствующей графе. В качестве примера возьмем рис. 49.

Следует отметить, что в правой верхней графе указаны 4 последовательных номера (35, 36, 37, 38). Вероятность такого совпадения весьма мала и потому, возможно, указывает на особую причину расхождения. Так, если на пример, результат одного испытания из 10 попадает в эту графу, вероятность проведения 4 последовательных линий будет равна всего (1/10)³

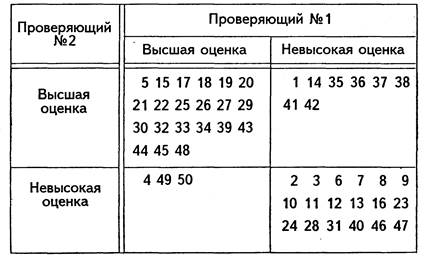
Рис. 49. Таблица 2 х 2 для проверок двумя проверяющими 50 изделий. Номера изделий показаны в таблице. Различие между данным рисунком и предыдущим состоит в том, что в данном рисунке показаны номера изделий.

Возможное использование метода дешевой проверки. Иногда в тестировании может быть полезна стратегия, хорошо известная в наблюдениях за течением болезни допустим, что расчеты показывают, что pk₂k₁ >; иными словами, 100% -е тестирование детали будет иметь минимальные совокупные издержки.

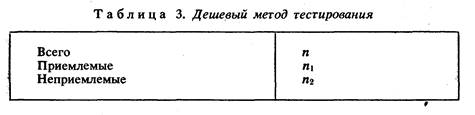
Дешевый метод доступен и может быть отлажен с тём, чтобы не пропустить детали, которые были бы отвергнуты при помощи совершенного метода. Сначала мы обследуем n деталей простым методом, затем делим выборку на два класса, приемлемые и неприемлемые пронумеровав их как n₁ и n₂ согласно таблице 3.

Мы сможем спокойно пускать в производство детали n которые дешевый метод классифицировал как приемлемые. (Предположительно, мы соответствующим образом отрегулировали дешевый метод). Затем подвергнем проверке совершенным методом детали, отвергнутые дешевым методом. Результаты занесем в таблицу 4.

Если стоимость тестирования деталей категории n₂ посредством совершенного метода не слишком велика, этим планом достигается довольно заметная экономия. Рас четы довольно просты; допустим, что:

К₁ - стоимость тестирования деталей совершенным методом

К_1’ – стоимость тестирования деталей дешевым методом

Таким образом, сплошное тестирование сэкономит

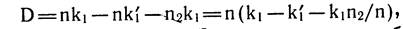, где величина в круглых скобках представляет собой разницу в издержках на единицу продукции. В качестве иллюстрации возьмем следующие цифры:

,

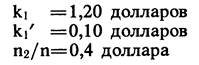тогда разница составит:

,

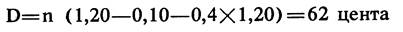что представляет собой примерно 50%-ю экономию.

Преимущество использования шкалы при сравнении. В случае если измерения производятся в таких единицах, как сантиметры, граммы, секунды, амперы, фунты, на квадратный дюйм и т. д., необходимо использовать более эффективный способ сравнения. Можно, например, отразить результаты n измерений посредством графика на плоскости с координатами х и у. Рис. 50 содержит четыре графика возможных сравнений результатов дешевого и совершенного методов тестирования. В данном случае для принятия решения достаточно значительно меньшей вели чины n, чем для таблицы 2Х2 на рис. 48. Точки на диагонали проведенной под углом в 45° означает согласованную работу обоих методов. Точки, лежащие вне этой прямой имеют противоположное значение. Исследование этой диаграммы быстро укажет на расхождение между этими методами и на его величину. Доводка дешевого метода с целью приведения его в большее соответствие с дорогим методом должна быть очевидной для всякого, кто обладает знанием и навыком пользования этими методами. 1340.

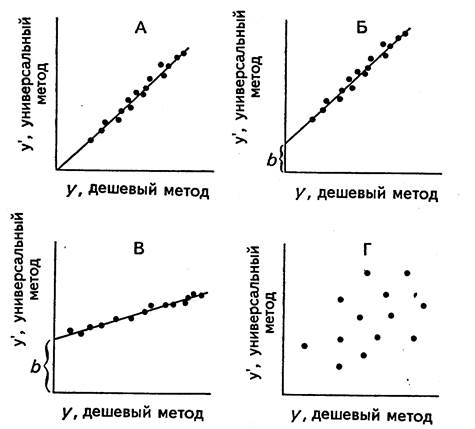
Рис. 50. Сравнения между универсальным методом и дешевым методом. Измерение параметра по двум методам дает точку на графике. Точка на линии в 45° означает наилучшее соотношение. (А) Точки лежат на или рядом с линией в 45°. В данном случае оба метода соотнося хорошо. (Б) Наклон линии близок к 45°, но существует разрыв. Какое-либо простое соглашение смогло бы привести два метода в соответствие. (В) Наклон линии отстоит довольно далеко от отметки в 45°, и существует разрыв. Простое соглашение могло бы привести оба метода в соответствие. Или можно путем некоторых корректировок при помощи простой формулы подправить дешевый метод. (Г) Точки разбросаны по всему графику, указывал на серьезные проблемы.

Можно также, учитывая простоту случая В на рис. 50, не отлаживать дешевый метод, а пересчитать его результаты совершенным методом. Так пусть

У ’= результат измерения совершенным методом

у = результат измерения дешевым методом того же изделия

m = наклон прямой наилучшим образом соответствующей соотношению (предположительно линейному) между двумя методами

и = положение точек по отношению к оси у’.

Удобным вариантом преобразования будет у’=у+mb в части В рис. 50.

Кстати говоря, согласованность результатов обоих методов вовсе не означает, что оба они верны. Это означает только то, что существует некая система измерения. Представляет интерес часть В рис. 50. Наклон прямой менее, чем 45° означает, что дешевый метод более чувствителен, чем совершенный. Если он сохранит превосходство, то мы, отбросив совершенный метод, будем пользоваться дешевым, отладив его соответствующим образом. (Предложено Питером Кларком из Хамменсдейла, провинция Наталь, на семинаре в Кейптауне в ноябре 1983 г.) Менее чем 45°-й наклон означал бы, что дешевый метод менее чувствителен, что обычно и наблюдается. В таком случае можно подогнать дешевый метод к совершенному, преобразовав его посредством уравнения у’= mу+b, где b означает наклон прямой.

Великолепный анализ ошибок измерения и точности инструментов содержится в разделе В-З книги Пособие по статистическому контролю качества выпущенной компанией Уестэрн Электрик в 1956 г. (см. ссылку в конце главы).

Опасности единодушия в контроле качества. Единство мнений, сложившееся после того, как каждый имел возможность изложить свою точку зрения и задать вопросы без опасений и без оглядки на окружающих (стр. 71) полезно как с точки зрения совместной работы, так и в смысле выгоды взаимодействия, появляющегося в результате взаимного обучения.

К сожалению, консенсус в контроле качества, а также и во многих других случаях может означать только то, что возобладало мнение одного человека, то есть консенсус отражает чье-то единоличное мнение.

Например, два врача могут проявить единодушие в отношении того, улучшилось ли состояние пациента, ухудшилось или осталось без изменений. Отчет подобного рода может всего лишь означать мнение старшего из медиков, в то время как более молодой будет счастлив возможностью сопровождать более старого и вникнуть в изрекаемые им мудрости. Теплым дружеским отношениям между этими двумя людьми может наступить конец, если у младшего из них появится слишком много собственных идей. Возможно, младший работает по временному контракту. Он не смеет рисковать своим местом в следующем году, посему он с готовностью соглашается и задает вопросы с осторожностью.

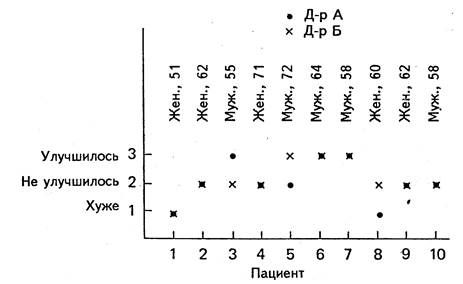
Рис. 51. Запись решений двух врачей, пациент за пациентом. Изучение совпадений и разногласий в зависимости от пациента может помочь обоим врачам понять, что они делают, и привести обоих к полному и независимому согласию.

Лучшим планом было бы, если бы каждый из врачей вел собственную запись своих наблюдений относительно состояния каждого пациента, отмечая улучшение, ухудшение или отсутствие изменений. Затем они могли бы сравнить свои записи в удобное для них время. Тогда молодой врач мог бы безо всяких конфронтаций задать вопросы о каждом пациенте по поводу совпадений и несовпадений во мнениях. Иными словами, предложенная система устраняет опасения молодого врача в связи с расспросами. Простая диаграмма, подобно рис. 51, обнаружит случаи согласия или несогласия (предложена автором, консультировавшим покойного доктора Франца Дж. Коллмэнна в Институте Психиатрии штата Нью-Йорк около 1960 г., и было принято последним).

Простые пометки на диаграмме, такие как возраст и пол больного, укажут молодому врачу, где ему требуется помощь.

Кстати, хорошая согласованность полученных независимых результатов, означает наличие системы, из этого вовсе не следует, что оба наблюдения правы. Верный ответ может быть получен только посредством методов, одобренных специалистами.

Сравнение работы двух контролеров. два контролера качества кожи в течение ряда лет вели запись совпадения оценок обёих из них относительно качества каждой упаковки кожи, изъятой в качестве контрольного образца из поступающих партий кожа. В ходе обсуждения они с готовностью осознали опасность единодушия и необходимость вести индивидуальные записи с тем, чтобы сравнить результаты и поучиться друг у друга в случае расхождения во мнениях.

Сорта кожи обозначаются 1, 2, 3, 4, 5. Первый сорт является лучшим. Был составлен следующий план:

1. Каждый контролер отбирает из каждой партии одну упаковку. Упаковка берется вразброс сверху, снизу и из середины. (Ранее мы это назвали механической выборкой без использования случайных чисел).

2. Каждый контролер независимо обследует выбранную упаковку и записывает результат.

3. Оба контролера независимо друг от друга обследуют упаковки и записывают результаты обследования каждой 20-й из них. Выбор образцов производится ими по очереди.

4. Результаты оформляются в виде диаграммы, упрощенная часть которой показана на рис. 52.

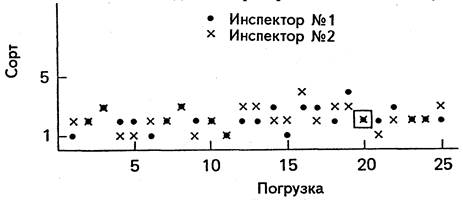
Рис. 52. Схема для демонстрации результатов двух инспекторов, работающих независимо. Разногласия не отражены на графике. Рамка у указателя 20 указывает на то, что оба инспектора проверяли одну и ту же упаковку кожи.

Возможны два источника расхождений между двумя рядами результатов: А) различия между двумя людьми, Б) различие между образцами. До сих пор (в течение по чти года) значительных расхождений между результатами не наблюдалось. Ни один контролер не отрывается от другого. Расхождения в результатах обследования каждой 20-й упаковки, проверяемой обоими контролерами, редки. Прочие случаи требуют более точных определений.

Еще раз следует подчеркнуть, что как уже отмечалось ранее, согласованность их оценок, не означает, что они верны: это значит лишь, что их отбор образцов и метод контроля образуют некую систему.

Еще одно замечание о графическом изображении. Способ представления результатов, отраженный на рис. 51 и 52, вполне применим к 4 или 5 контролерам. (Шесть коытролеров создают проблему многообразия символов). Я использовал этот способ для обозначения тремя символами. © О. Х) качественных характеристик, полученных на материале, взятом (1) в начале, (2) в середине и (3) в конце одного и того же процесса. Собственно говоря, эти три символа появлялись в одном и том же вертикальном соотношении в 12-ти случаях, не считая соединения О и Х. Это повторяющееся соотношение означало возможность того, что (а) компоненты в одной партии не были достаточно перемешаны или что (б) смесь успевала значительно «состариться» в ходе производства.

Упражнения

Упражнение 1. Дано: емкость с красными и белыми бусинами, Пропорция красных бусин р, белых – q (рис. 53).

Шаг 1. Методом случайных чисел с замещением изъятых бусин извлечь из емкости партию размера N. Получаем:

N всего

Х красных

N—Х белых

Шаг 2. Методом случайных чисел без замещения взять выборку объемом n. Получаем:

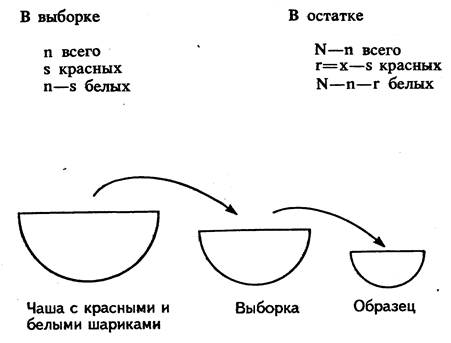
Рис. 53. Выборка берется из чаши с красными и белыми шариками. Образцы затем берутся из выборки. Замена каждого шарика, заложенного в выборку, подтверждает постоянство соотношения р в выборке при каждом отборе.

Шаг 3. Вернуть бусины из выборки в партию.

Шаг 4. Повторить Шаги 1, 2 и З несколько раз, поддерживая постоянный объем партии и объем выборки из нее. Запишите результаты для r и s.

Теоретическое распределение r и s будет

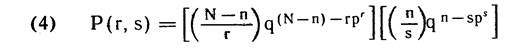
Выводы: (а) количество красных бусин в выборке объемом n и количество красных бусин в остатках биноминально распределены примерно в одной пропорции р и (b) они не связаны друг с другом. Иными словами, количество r красных бусин в остатках, соответствующих вы боркам с s = 17 дефектных единиц, будут иметь точно та кое же распределение, что и красные бусины в остатках, соответствующих образцам с s = О дефектных единиц.

Это теорема ужасает. Она показывает, что если отдельные дефектные единицы являются независимыми, что практически должно быть в случае, когда процесс находится в рамках хорошей статистической нормs, то успех любой попытки разработки плана приемки будет соответствовать результатам подбрасывания монеты с целью отбора остатков, подлежащих сплошной проверке. (Подбрасывание монеты несравненно дешевле, нежели тестирование образцов изделия).

Вместо изъятия выборки из партии изделий можно просто разделить партию на две части, выборку и остаток, методом случайных чисел.

Упражнение 2. Если распределение дефектных изделий в партиях более комплектное по сравнению с биномиальным и если правило приемки остатка основано на тестировании выборки, то следует ввести правило принимать остаток таким, как он есть, когда в выборке много дефектных изделий, и отвергать и подвергать сплошной проверке, если в выборке обнаружено мало дефектных изделий и если их не обнаружено вовсе, а не использовать обычные правила, противоположные данному.

Простейший способ понять суть вышеизложенного это рассмотреть случай, когда все поступающие партии исходного продукта содержат идентичное количество дефектных единиц. Дефектные единицы, не попавшие в остаток, окажутся в выборке, и наоборот. Следовательно, наличие значительного количества дефектных единиц в выборке указывает на их малое количество в остатке.

И.Д. Хилл (1960) указал второй способ производить партии с единообразным уровнем качества, допустим, 20 машин производят одно и то же изделие, из них 19 вы пускают изделия без брака, а одна выпускает только брак. Возьмите по одному изделию от каждой машины, таким образом вы получите партию изделий. Тогда каждая партия из 20 изделий будет иметь ровно 5% брака.

Партии изделий с почти стабильным качеством - не такая уж редкость. Для примера приведем блок из, скажем, 12 конвейерных дисков. Они перемещают металлические листы для штамповки. Один из конвейерных дисков неисправен. Почти вся произведенная с его помощью продукция оказывается бракованной. Остальные 11 в полном порядке, партии из 12 последовательно произведенных изделий будут содержать около 1/12 или 8,3% брака.

Упражнение 3. Доказательство правила все или ничего. Изымите случайно (методом случайных чисел) деталь из партии продукции. Назовем ее деталь i. Она окажется бракованной или наоборот. Следует ли предварительно проверить ее или же запустить в производство без проверки независимо от того, дефектная она или нет? Изобразим средние совокупньте издержки в виде таблицы (таб лица 5).

Мы видим, что Да и Нет равны, если p = k₁/k₂. Это свойство было названо Александром Мудом точкой перелома качества. В точке перелома совокупные издержки равны как для Нет, так и для Да. Далее мы наблюдаем, что если p< k₁/k₂ в случае Нет общие издержки будут ни же, а если p> k₁/k₂ меньшие издержки обеспечиваются в случае да. (см. рис. 54).

Очевидно, что если наихудшая партия, которая поступит, например, на будущей неделе, расположится слева от точки перелома, то все прочие партии окажутся лучше и расположатся еще дальше влево. Ясно, что в этом случае отмена контроля обеспечит минимум средних совокупных издержек — Случай 1.

Если же, с другой стороны, лучшая партия, которая должна поступить, расположится справа от точки перелома, все остальные партии будут еще хуже и расположатся еще дальше вправо. Это Случай 2. Минимальные средние совокупные издержки будут достигнуты 100 % -й проверкой всех партий.

Таким образом, минимальные средние совокупные издержки лежат на ломаной линии ОСД. Если значения p близки к точке В, то есть точке перелома, различия между отсутствием контроля и 100% -м контролем будут незначительными.

Упражнение 4. Минимальные средние совокупные издержки в случае множественных комплектующих допустим, у нас всего М комплектующих. При этом рi —средняя доля брака для комплектующей i, а, Кi — издержки на тестирование одной комплектующей. Дополнительные издержки, связанные с отказом собранного узла, обозначим через К, предположительно равное в случае любой комплектующей. (Некоторое изменение условных обозначений необходимо в связи с тем, что мы будем использовать символы к₂ для обозначения издержек тестирования комплектующей 2). Следует ли нам проверить все комплектующие или только часть? Если только некоторые, то какие именно? Используем приближенное значение Уравнения 3, стр. 433.

Различие между двумя планами будет в пользу Плана 2 на сумму

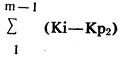
Какие комплектующие мы должны подвергнуть проверке и какие оставить без проверки, чтобы свести общие издержки к минимуму? Иными словами, каким образом мы можем максимизировать разницу между двумя планами? Ответ очевиден. Расположите М членов прогрессии.

в нисходящем порядке величины. Члены прогрессии начнутся с положительной величины, будут уменьшаться, пересекут нулевую отметку и будут продолжать уменьшаться. для достижения минимальных средних издержек величина суммы в вышеприведенной формуле должна быть максимальной. Соответственно, правило минимальных средних совокупных издержек формулируется следующим образом:

1. Комплектующие, для которых кi — Крi>0 являет- позитивным, не проверяются.

2. Проверьте все остальные комплектующие, для которых кi — крi является отрицательной величиной.

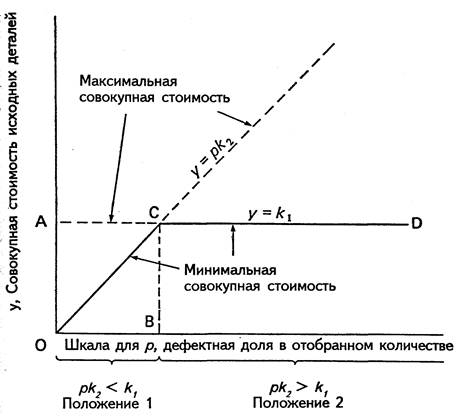
Рис. 54. График, отражающий минимальную совокупную стоимость детали в выборке бракованных деталей, как функцию качества исходных деталей р. Минимальный процент брака располагается вдоль ломаной линии ОСД. Перелом С возник при переломе качества, точка В, где p = k₁/k₂. Общая стоимость доведена до максимума путем использования 100 % проверки, где никакая проверка не даст минимальной совокупной стоимости и наоборот.

Следует поработать со всеми поставщиками, чтобы принести уровень качества всех комплектующих к статистической норме и уменьшить ее до рi. Успех этих усилий снизит совокупные издержки и позволит время от времени отказываться от проверки некоторых комплектующих.

Замечание 1. Простой сдвиг от отрицательной к положительной величине вызовет лишь незначительное сокращение издержек, в то время как большой скачок от значительной отрицательной величины к значительной положительной приведет к существенному сокращению издержек.

Замечание 2. Можно сказать, что каждая комплектующая имеет точку перелома качества, определяемую рi=Кi/К. Таким образом, наш результат для множественных комплектующих всего лишь повторяет План 1 и План 2 для простой комплектующей.

Замечание 3. С комплектующей, у которой распределение доли дефектных изделий располагается по обе стороны от точки перелома качества, следует поступать точно также как и с одной комплектующей.

Замечание 4. Используйте 100%-ю проверку каждой комплектующей, которая не находится в пределах хорошей статистической нормы: тем более, если она находится в состоянии хаоса.

Упражнение 5. (Задача показать, что если качество исходного материала стабильно лежит преимущественно на одной стороне от точки перелома качества, принятие любого плана контроля, кроме правил все или ничего рискует повысить совокупные издержки). Допустим, что мы проверяем долю f партии исходных материалов со средним уровнем брака р. Отбор деталей производится методом случайных чисел. В таком случае средние совокупные издержки на единицу подлежащего проверке материала и дополнительные издержки на ремонт и повторное тестирование собранного блока, вышедшего из строя из-за неисправной комплектующей, составит:

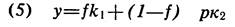(пренебрегая издержками kp).

Вопрос заключается в том, какой должна быть вели чина f чтобы свести к минимуму у? Отметим для на чала, что у=k₁ независимо от величины f в точке, где p = k₁/k₂ (т. е. в точке перелома).

Слева от точки перелома p < k₁/k₂ Удобно переписать уравнение 5 в следующем виде

(6)

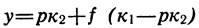
Очевидно, что если мы позволим изменяться в пределах от О до 1 слева от точки перелома качества, то у будет изменяться от своего минимума, равного pk₂ до k₁. Иными словами, любой контроль качества слева от точки перелома (p < k₁/k₂) только увеличит совокупные издержки. Очевидно, что любой план приемки в этом случае удвоит или утроит минимальные совокупные издержки.

Прежде чем исследовать область от точки перелома, где p > k₁/k₂, перепишем уравнение 5 следующим образом:

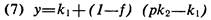
Если мы позволим f изменяться от О до 1 в этой области, у будет принимать значения от рk₂ и ниже до своего минимума k₁. Иными словами, 100%-я проверка справа от точки перелома качества приводит к минимальным совокупным издержкам. Менее чем 100%-я проверка (т. е. при f<1) увеличит средние совокупные издержки -по сравнению с минимальными.

На стр. 439 был приведен пример, предложенный Уильямом Дж. Лацко. Обратимся еще к одному примеру.

Иллюстративный пример. Некая компания принимает в качестве исходного материала алюминиевые заготовки для производства жестких дисков партиями по 1000 штук.

Ранее первым шагом по принятии партии был визуальный осмотр образцов в количестве 65 единиц, изъятых из партии наугад. Опыт показывает, что исходная заготовка, не прошедшая визуальный контроль, вызовет отказ готового диска, если ее использовать в производственном цикле. Каждая заготовка, отвергнутая в ходе визуального контроля, заменялась исправной.

Средняя пропорция заготовок, отвергавшихся в ходе визуальной проверки, составляла примерно 1 из 40, т. е. 0,025. Было принято за правило отвергать всю партию, если 5 или более заготовок в выборке признавались, непригодными (5 было верхним пределом, равным 3-м сигмам). Согласно отчетам, партии исходного материала чрезвычайно редко отвергались: на ближайшее будущее, соответственно, могла быть принята умеренная статистическая норма.

Таким образом, средняя доля дефектных, с точки зрения визуальной проверки, заготовок, используемых в производственном цикле, составляла 0,025 — (65/1000) Х Х0,025=0,023.

Полная стоимость визуального контроля составляет 7 центов на заготовку.

1 % заготовок приводится в негодность в ходе подготовки к визуальной проверке, а также в ходе самой проверки.

Описанная выше проверка касалась только дефектов, которые могли быть обнаружены визуально. Прочие дефекты, необнаруживаемые визуально, являются причиной отказа одного диска из ста в ходе окончательного тестирования. Это накладные издержки, общие и постоянные, независимо от пропорции исходного материала, подвергаемого визуальной проверке. По этой причине мы не рассматриваем их в нижеприведенной таблице издержек.

Стоимость, добавляемая в ходе изготовления диска, равна 11 долларам. Стоимость заготовки в производимом диске который не прошел контроль, подлежит рекламации: таким образом, потери на один диск составляют 11 долларов, не считая издержек на рекламацию. Пусть f доля материала, проверенного по описанному плану (=65/1000=0,065)

k₁ — стоимость визуальной проверки одной заготовки (=7 центов)

В — стоимость одной заготовки (2 доллара)

K₂ — добавленная стоимость (11 долларов) на одно изделие

р — среднее качество исходного материала в терминах визуально обнаруживаемых дефектов (= 0,025)

р’ - средняя доля дисков, неисправных из-за прочих дефектов (=0,01)

р” - средняя доля заготовок, допущенных в производство согласно описанному плану, которые однако. не прошли бы визуальный контроль, если бы были подвергнуты проверке, (0,025[1—65/1000] = 0,023).

F — доля заготовок, приведенных в негодность в ходе подготовки их к визуальной проверке, а также в ходе самой проверки (=0,01).

Теперь мы можем составить таблицу 6 для определения издержек.

Заключение. Разрыв между 100%-й проверкой и используемым планом столь велик, что вполне можно порекомендовать немедленно внести в него изменения. Эта рекомендация необходима в силу значительных отклонений в доле брака и затрат в вышеприведенной таблице.

Тем временем продолжаются совместные усилия поставщика и производителя по улучшению качества заготовок в надежде пересечь точку перелома с тем, чтобы отказаться от визуальной проверки и связанной с ней подготовки заготовок к проверке.

Примечание: Точка перелома отнюдь не выражается здесь простым отношением k₁/k₂, как было до сих пор, однако мы не будем входить в эти сложности.

Упражнение 6. Оно демонстрирует бессмысленность следующего правила, предъявленного одним большим концерном поставщикам:

Вследствие того, что мы полагаемся на выборочную проверку для определения приемлемости поставляемого материала, одна дефектная единица поставки приводит к отказу от целой партии.

Комментарии: (1) собственно говоря, большая часть партий направляется прямо в производственный цикл, пройдя проверку или без проверки. Клиент не может позволить себе отсрочек на проверку или на возвращение партии поставщику. (2) Если к k₁>pk₂, то выборочная проверка повысит совокупные издержки сверх минимума, достижимого при отсутствии про верки. К чему повышать издержки? (3) Если k₁< pk₂, то минимальные совокупные издержки достигаются в результате 100%-й, а не выборочной проверки. Опять же, к чему повышать издержки? (4) Если распределение качества исходных материалов полностью выпадает из статистической нормы и располагается вокруг точки перелома, то лучшим решением проблемы будет либо 100%-я проверка, либо использование правил Джойс Орсини (стр. 422). В таком случае, выходите из этого прискорбного положения. Работайте с поставщиком в целях улучшения качества, с тем, чтобы прийти к Случаю 1 (k₁< pk₂₎ и продолжайте совершенствование процесса, добиваясь, если возможно, нулевого уровня брака. (5) Короче говоря, цитированное выше требование отстало от жизни, неэффективно и гарантирует низкое качество при высоких издержках.

Упражнение 7. Оценка величины к. Мы исходим из допущения, что стоимость проверки детали, взятой из совокупной поставки S, равна обычной стоимости проверки детали, взятой из партии размером N. Пусть Хi = 1, если это деталь дефектная, либо же Хi = 0, если нет. Допустим, что Хi = 1, в таком случае деталь i оказывается дефектной. Тогда мы должны взять из совокупной поставки S ёще одну деталь и проверить ее: издержки составят k₁. Она также может оказаться дефектной, и нам придется брать и проверять следующие, и так до тех пор, пока нам не попадется исправная деталь. Мы можем отразить эти возможности посредством дерева вероятностей на рис, 55. Средние издержки будут, очевидно, равны:

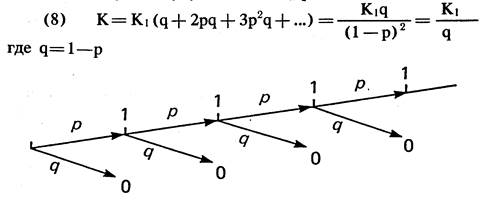
Рис. 55. Проверка деталей с показателем вероятности р при х_i = 1, дефектная, и показателем вероятности ‚ при х_i = 0, не дефектная.

Общие средние совокупные издержки на проверку одной детали и замену дефектной детали исправной составят k₁+pk = k₁/q

Так как в большинстве случаев р мало, q будет близко к единице, в каковом случае мы можем заменить выражение k₁/q на k₁.

Упражнение 8. Условные обозначения

N = количество единиц в партии

n = количество единиц в выборке (предположительно взятых методом случайных чисел из партии) - с заменой дефектных единиц на исправные

р = средняя доля дефектного исходного материала; эта величина р представляет собой приблизительный прогноз средней величины на ближайшие несколько недель.

q =1 — р

р’ = средняя доля дефектных единиц в отвергнутых партиях, подлежащих сплошной проверке

р” = средняя доля дефектных единиц в принятых партиях, которые будут отправлены непосредственно в производство

k₁ = стоимость проверки одной детали

k₂ = стоимость разборки, ремонта, повторной сборки и тестирования сложного изделия в случае его отказа из-за дефектной детали, допущенной в производственный цикл

Р = средняя доля партий, предназначенных для сплошной проверки на начальной стадии контроля качества (т. е. отвергнутых).

Q = 1—Р = доля партий, принятых при первоначальной проверке.

Независимо от плана приемки, можно быть уверенным, что:

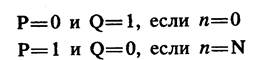
Теперь посмотрим, что будет происходить со средней партией, если мы прибегнем к этому плану.

n деталей без дефектов, неотправляемые в производство, (N — п) (детали, неотправляемые непосредственно в производство без проверки; среднее качество = р

(N—п) Р детали отвергнутые и подлежащие сплошной проверке. Затем исправные из их числа будут допущены к производству.

а) средние совокупные издержки составят:

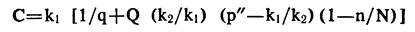
б) Если p < k₁/ k₂ то p” — k₁/ k₂ будет отрицательной величиной, и мы достигнем минимальных общих издержек при п = 0 (Случай 1).

с) Если p > k₁/ k₂ и если мы преуспели в нахождении плана, обеспечивающего отрицательное значение величины р”— k₁ k₂ то средние совокупные издержки будут ниже издержек при 100%-й проверке.

д) Но если, несмотря на все наши усилия, наш план сохраняет положительное значение величины р” — k₁/k₂ то совокупные издержки превысили бы расходы в случае 100%-й проверки исходного материала. Эта та самая западня, избегать которую мы учились на примере 5.

Рис. 56. Масса в 50 шариков останавливается механически лопаткой с 50 отверстиями в ней из большого количества красных и белых шариков. Мы определяем 20 шариков как образец, а оставшиеся 30 - как остаток.

Приложение к главе 15