Полная структура моделируемой системы

Общая структура разработанной системы моделирования включает следующие блоки:

• Аналоговая часть. Задается в виде передаточной функции W(s).
• АЦП. Для этого блока задается разрядность (N=8,10,12,14,16);
• Датчик (SENSOR). Блок построен таким образом, что позволяет моделировать погрешность датчика, закон изменения погрешности задается в виде формулы.
• Цифровой регулятор (его структура описана выше).
• Задающий генератор (PRESSURE GENERATOR) - генерирует задающее воздействие.
• Генератор возмущающих воздействий (TEMPERATURE GENERATOR).

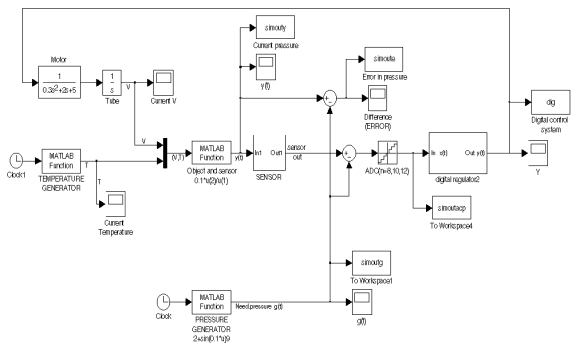
Рис 3.3 Общая структура исследуемой системы.

Особенностью данной структуры является то, что она включает в себя как дискретную, так и аналоговую части, что позволяет с наибольшей достоверностью исследовать процессы, протекающие в системах с цифровыми регуляторами и оценить достаточную разрядность АЦП и точность датчиков для обеспечения заданного качества процесса регулирования.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

На начальном этапе выполнено моделирование системы для П-регулятора. Параметры регулятора задаются в следующем виде:
Kp = 1
Td = 0 (исключается производная)
Ti = 10000000000000 (исключается интеграл)
T = 0.2 (период квантования сигнала датчика)
время моделирования - 100 с
задающее воздействие - гармонический сигнал (рис 3.4)

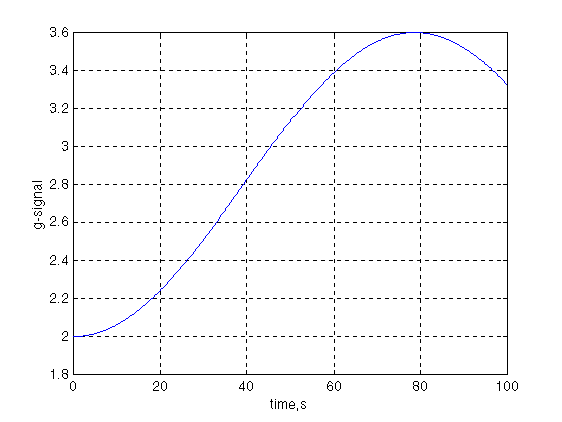
Рис 3.4 Задающее воздействие.

Качество регулирования системы будем оценивать, используя среднеквадратичную оценку погрешности реакции системы на задающее воздействие. С этой целью строим графики ошибки регулирования для различной разрядности АЦП (погрешность датчика в данном случае не учитывается).

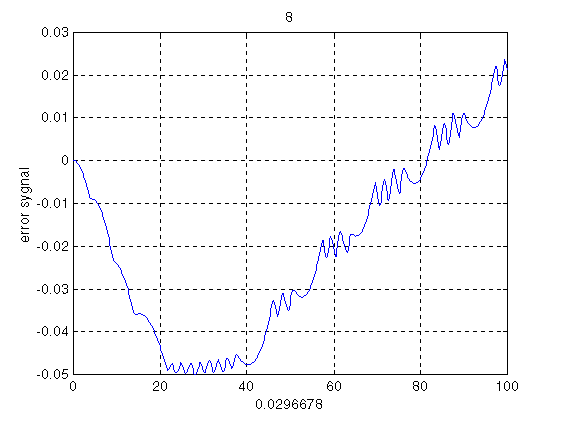
Рис 3.5 Ошибка регулирования при Nацп=8 разрядов.

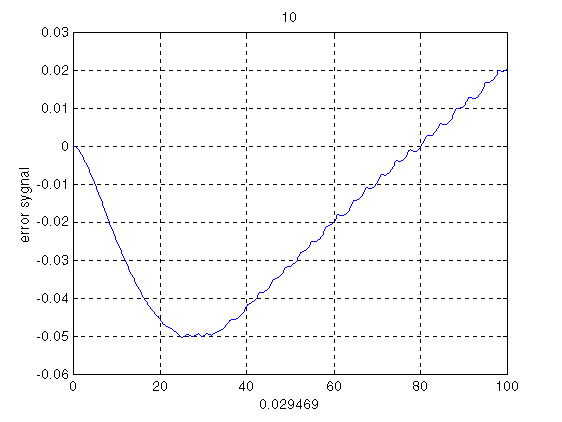
Рис 3.6 Ошибка регулирования при Nацп=10 разрядов.

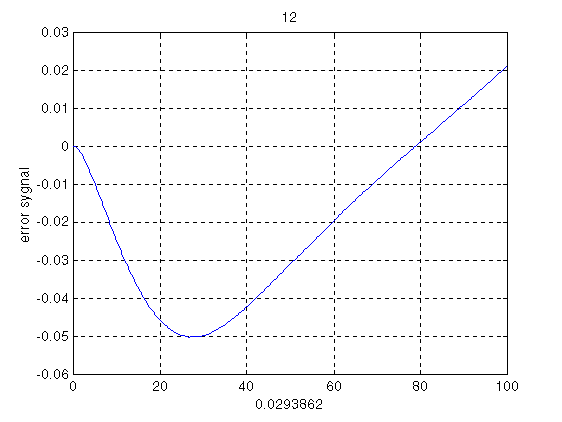
Рис 3.7 Ошибка регулирования при Nацп=12 разрядов.

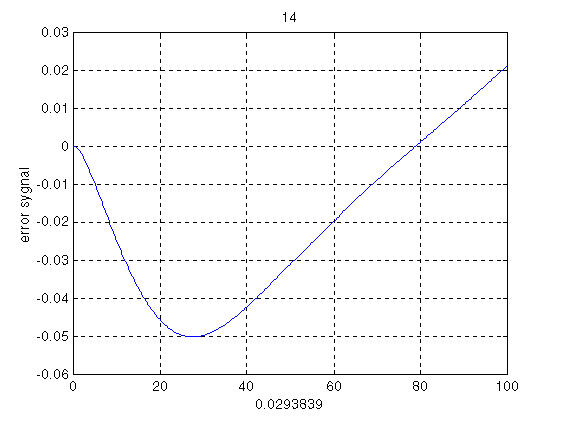
Рис 3.8 Ошибка регулирования при Nацп=14 разрядов.

Для сравнения результатов удобно вычислить среднеквадратичную ошибку регулирования для случая, когда разрядность АЦП бесконечно велика, и принять ее за идеальную (минимальную для данного закона регулирования и коэффициентов регулятора). Эта ошибка составляет 0.0293778 (значение получено при Nацп=32 разряда). Результаты моделирования можно свести в таблицу:

Разрядность АЦП
ошибка регулирования	0.0296678	0.029469	0.0293862	0.0293839	0.0293778

Рассчитаем относительную погрешность, вносимую АЦП. Значением без погрешности АЦП будем считать значение ошибки регулирования при Nацп=32 разряда. График зависимости погрешности, вносимой АЦП, от разрядности АЦП будет иметь следующий вид:

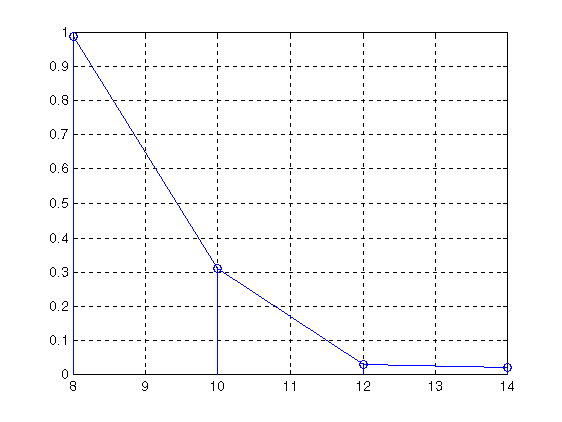
Рис 3.7 Погрешность, вносимая квантованием входного сигнала.

Полученная зависимость показывает, что увеличение разрядности АЦП имеет смысл до определенного предела. Величина этого предельного значения определяется качеством регулирования и во многом зависит от погрешности датчика (т.к. в данном случае погрешность датчика равна 0, то и кривая на графике стремится к 0). Если погрешность датчика не нулевая, данная кривая при Nацп стемящемся к бесконечности будет приближаться к некоторому значению, которое отлично от 0 и определяется погрешностью датчика.

ЗАКЛЮЧЕНИЕ

На данном этапе выполнения магистерской диссертации получены следующие результаты:

• разработана структура цифрового ПИД-регулятора в среде MatLAB;
• разработана структура цифровой системы регулирования с использованием MatLAB;
• выполнено моделирование П-регулятора.

Анализ результатов моделирования показывает необходимость дальнейшего исследования проблемы (для ПИ-, ПД- и ПИД-регуляторов) с моделированием погрешности датчика и полной погрешности АЦП.

Полученные зависимости наглядно показывают необходимость тщательного выбора АЦП и датчиков с целью обеспечения необходимой точности с минимальными затратами. Разработанная структура модели цифровой системы регулирования может использоваться как базовая при моделировании подобных систем.