Входные и взаимные проводимости ветвей. Входное сопротивление.

Входные и взаимные проводимости ветвей используют при выводе общих свойств линейных электрических цепей и при расчете цепей по методу наложения (см.формулу (2.13)).

На рис. 2.9а изображена так называемая скелетная схема пассивной цепи. На ней показаны ветви и узлы. В каждой ветви имеется сопротивление. Выделим в схеме две ветви: m и k. Поместим в ветвь т ЭДС Е_т (других ЭДС в схеме нет). Выберем контуры в схеме так, чтобы k-ветвь входила только в k-контур, а m-ветвь - только в m-контур. ЭДС Е_т вызовет токи в ветвях k и m:

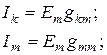(2.14)

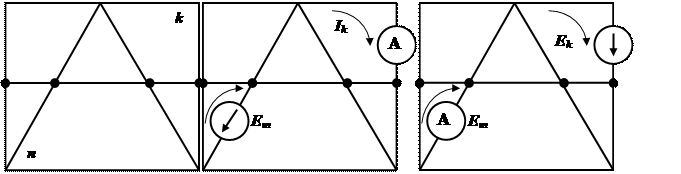
а б в

Рис.2.9

Коэффициенты g имеют размерность проводимости.

Коэффициент g с одинаковыми индексами (g_mm) называют входной проводимостью ветви (ветви m). Он численно равен току в ветви m, возникшему от действия ЭДС Е_т = 1В (единичной ЭДС): I_m, = 1 g_mm.

Коэффициенты g с разными индексами называют взаимными проводимостями. Так, g_km есть взаимная проводимость k- и m-ветвей. Взаимная проводимость g_km численно равна току в k-ветви, возникающему от действия единичной ЭДС в m-ветви. (Входные и взаимные проводимости ветвей можно определить и иначе: вход проводимость m-ветви - это коэффициент пропорциональности между током и ЭДС этой ветви (при отсутствии ЭДС в других ветвях схемы); взаимная проводимость ветвей k и m - коэффициент пропорциональности между током k-ветви и ЭДС m-ветви при oti сутствии ЭДС в других ветвях схемы).

Входные и взаимные проводимости могут быть определены расчетным и опытным путями.

При их расчетном определении составляют уравнения по методу контурных токов, следя за тем, чтобы ветви, взаимные и входные проводимости которых представляют интерес, входили каждая только в свой контур. Далее находят определитель системы D и по нему необходимые алгебраические дополнения:

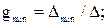(2.15)

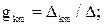(2.16)

По формуле (2.16) g_km может получиться либо положительной, т отрицательной величиной. Отрицательный знак означает, что ЭДС Е направленная согласно с контурным током в m-ветви, вызывает ток в k-ветви, не совпадающей по направлению с произвольно выбранным правлением контурного тока I_k по k-ветви.

При опытном определении g_mm и g_km в m-ветвь схемы (рис. 2.9б) включают источник ЭДС Е_m, а в k-ветвь - амперметр (миллиамперметр). Поделим ток I_k на ЭДС Е_m, и найдем значение g_km. Для определения входной проводимости g_mm ветви m необходимо измерить ток этой ветви, вызванной ЭДС Е_m. Частное от деления тока m-ветви на ЭДС m-ветви и дает g_mm.

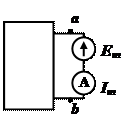
Рис.2.10.

Выделим m-ветвь, обозначив всю остальную часть схемы (не содержащую ЭДС) некоторым прямоугольником (рис. 2.10). Вся схема, обозначенная прямоугольником, по отношению к зажимам ab обладает некоторым сопротивлением. Его называют входным сопротивлением. Входное сопротивление m-ветви обозначим R_вх.m . Тогда

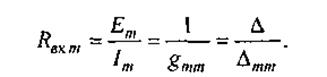(2.17)

Таким образом, входное сопротивление m-ветви есть величина, обратная входной проводимости этой ветви. Его не следует смешивать с полным сопротивлением m-контура в методе контурных токов.

Теорема взаимности.

Теорема взаимности формулируется следующим образом: для любой линейной цепи ток в k-ветви, вызванный источником ЭДС Е_m, находящимся в т-ветви, I_k = Е_m g_km равен току 1_т в т-ветви, вызванному источником ЭДС Е_к (численно равной ЭДС Е_m), находящимся в k-ветви, I_т = Е_к g_mk.

Для доказательства теоремы взаимности обратимся к рис. 2.9а. Выделим две ветви схемы: к- и m-ветви. Включим в ветвь т источник ЭДС Е_m в ветвь к - амперметр А. Амперметр для измерения тока 1_к включаем только для наглядности; сопротивление амперметра полагаем равным нулю. Пусть каждая из ветвей к и т входит соответственно только в k- и m-контуры. Поэ-тому по методу контурных токов 1_к =Е_т Δ_km/Δ. Поменяем местами ис-точник ЭДС и амперметр, т. е. источник ЭДС переместим из т- в k - ветвь и назовем теперь Е_к, а амперметр - из к- в m-ветвь. В этом случае ток I_m = Е_к Δ_тк /Δ.

Так как Е_к = Е_т, а Δ_тк =Δ_кт в силу симметрии определителя системы Δ относительно главной диагонали , то ток 1_к в схеме на рис 2.9б равняется току 1_m в схеме на рис. 2.9в.

При практическом использовании теоремы взаимности важно иметь в виду взаимное соответствие направлений токов и ЭДС в схемах на рис. 2.9б, в.

Так, если ЭДС Е_к источника ЭДС, находящегося в k-ветви схемы (рис. 2.в), направлена согласно с контурным током 1_к (рис. 2.9б), то положительное направление отсчета для тока I_т (рис. 2.9в) будет совпадать с положительным направлением контурного тока по ветви т (ЭДС Е_т в схеме на рис. 2.9б направлена по I_т).

Для нелинейных цепей теорема (принцип) взаимности невыполнима. Цепи, для которых не выполняется принцип взаимности, называют необратимыми.

Теорема компенсации.

Рассмотрим два варианта этой теоремы. В любой электрической цепи без изменения токораспределения сопротивление можно заменить:

1) источником ЭДС, ЭДС которого численно равна падению напряжения на заменяемом сопротивлении и направлена встречно току в этом сопротивлении;

2)источником тока J, ток которого численно равен току в этом сопро-тивлении и имеет то же направление, что и ток I.

Номер ветви соответствует индексу ЭДС.

Для доказательства теоремы компенсации выделим из схемы одну ветвь с сопротивлением R, по которой течет ток I, а всю остальную часть схемы условно обозначим прямоугольником (рис. 2.11а).

Если в выделенную ветвь включить два одинаковых и противоположно направленных источника ЭДС Е, ЭДС которых равна падению напряжения на сопротивлении R под действием тока I (Е = I R; рис. 2.11б), то ток I в цепи от этого не изменится. Убедимся, что разность потенциалов между точками а и с на рис. 2.11б при этом равна нулю. Действительно,

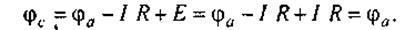
Если φ_с =φ_а, то точки а и с можно объединить в одну, т. е. закоротить участок ас и получить схему, где вместо сопротивления R включен источник ЭДС Е (см. рис. 2.11в).

Схема, соответствующая второму варианту теоремы, изображена на рис. 2.11г. Чтобы прийти к ней, заменим последовательно соединенные R и Е на участке ас (см. рис. 2.11б) параллельным соединением источника тока J = E/ R = I и сопротивления R. Так как U_ac = 0, то ток через R будет отсутствовать и потому R можно удалить из схемы.

Если ЭДС Е участка bc включить в состав источника тока, то получим схему, где напряжение U_ba = -I R (рис. 2.11г).

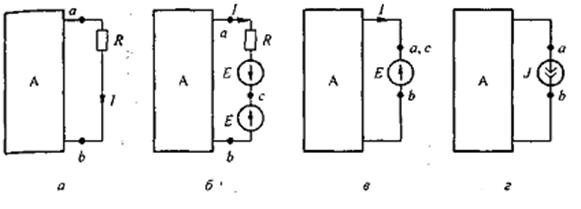
Рис.2.11