Сложного программного комплекса

Надежность сложных программных комплексов

(магистр)

Лекция №8. Модели оценивания и обеспечения надежности

сложного программного комплекса

В связи с массовым внедрением средств вычислительной техники в различные сферы человеческой деятельности, наблюдается устойчивая тенденция роста сложности программного обеспечения. Чрезмерная сложность вновь создаваемых программных комплексов, высокая стоимость программ и сравнительно низкий уровень качества их производства не позволяют исключить возможность возникновения ошибок, приводящих к нарушению работоспособности вычислительных средств, снижению их производительности. Следствием этого является отказ, нарушение работоспособности систем, использующих вычислительные средства [8].

Используя термин “надежность программного обеспечения” аналогично понятию “надежность аппаратуры”, необходимо помнить, что “отказы программного обеспечения” в системах, как результат проявления ошибок при его использовании имеют совершенно другую физическую природу, чем отказы техники. Однако, это не может служить причиной невозможности использования терминов и показателей надежности при исследовании качества программного обеспечения [9]. В частности, это оправдывается и необходимостью решения задачи распределения ресурсов или затрат между самими вычислительными средствами и их программным обеспечением при достижении заданного значения показателя надежности. Одним из важнейших общих показателей надежности, представляющих интерес для практики, является вероятность его безошибочного функционирования.

Проверка правильности функционирования разработанного программного обеспечения (корректности, устойчивости) и удовлетворение его требованиям спецификации осуществляется на этапе отладки и тестирования. Как правило, основным фактором отладки является затраченное на нее время. Поэтому в ряде моделей оценивания надежности программ наряду с необходимым временем их функционирования при решении конкретных задач рассматривается и второй временной фактор – время отладки этих программ до использования по назначению.

Для удобства анализа показателей надежности сложных программных комплексов целесообразно представить их в виде совокупности менее сложных компонент, обычно называемых программными модулями. Программный модуль, в свою очередь, может быть разделен на более мелкие части и т.д. Таким образом, программный модуль является аналогом элемента расчета теории надежности. Обычно он представляет собой логически самостоятельную программу и вводится, исходя из соображений исследователя[10].

При исследовании надежности функционирования программного комплекса обычно необходимо решить две задачи. Первая – по заданной структуре комплекса, состоящего из совокупности программных модулей, имеющих показатели надежности, найти показатель надежности программного комплекса. Эту задачу традиционно назовем прямой.

Наряду с первой может решаться вторая задача – достижение максимального (минимального) значения показателя надежности при некоторых ограничениях на ресурсы, в качестве которых выступают время, стоимость и др. Или решается задача минимизации величины ограничения при достижении требуемого (заданного) значения показателя надежности. Любую из этих задач будем называть обратной. Рассмотрим решение этих задач.

Постановка задачи. Дан программный комплекс, состоящий из М отдельных модулей, связанных между собой. По структуре комплекса строится стохастический граф, содержащий М+2 вершин. Вершина О означает исток, а вершина М+1 – сток графа. Каждый модуль инициируется на решение с заданной вероятностью, зависящей от цели функционирования или значений исходных данных. Прямая задача заключается в нахождении вероятности безошибочного решения задачи программным комплексом, если известны вероятности безошибочных решений задач всех модулей. Обратная задача заключается в том, что необходимо найти максимум вероятности безошибочного решения задачи программным комплексом при известном ограничении на общее время отладки всех программных модулей, а также в определении минимального времени отладки всего программного комплекса при заданной вероятности его безошибочного функционирования.

Прямая задача. Воспользуемся методом расчета вероятностно-временных характеристик пребывания заявки в сети массового обслуживания [11] для определения вероятности безошибочного решения задачи сложным программным комплексом, состоящим из совокупности модулей. Предполагаем, что модули статистически независимы.

Рассмотрим матрицу G=G(t), t=(t₀, t₁, t₂,…, t_М+1), элементами которой являются произведения p_ijP_i(t_j); i,j – (0,1,2,…,М+1), где p_ij - вероятность перехода от i-го модуля к j-му, а P_i(t_j) - вероятность безошибочного функционирования i-го модуля в течение времени t_j.Так как нулевая и (М+1)-я вершины фиктивные, то предполагаем, что время нахождения в них равно нулю, а вероятность безошибочной работы равна единице.

Введем понятие шага, понимая под ним единичный переход от одного модуля к другому. Для нахождения вероятности безошибочной работы за два шага нужно просуммировать с соответствующими вероятностями произведения вероятностей по всем путям, содержащим две вершины. Это достигается возведением матрицы G в квадрат. Возводя матрицу G в куб, получаем вероятности безошибочного функционирования за три шага и т.д. Далее строим матрицу

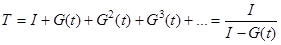, (8.1)

где I - единичная матрица.

Элемент матрицы Т с номером (0, М+1) представляет собой выражение для вероятности безошибочной работы всего программного комплекса с учетом всех возможных последовательных вызовов отдельных модулей.

Вероятность безошибочной работы комплекса будет равна [12],

Y(t) = Q(t) / R(t), (8.2)

где Q(t) – алгебраическое дополнение элемента (М+1, 0) матрицы (I-G(t)), а R(t) - ее главный определитель.

После выполнения необходимых преобразований получим искомое выражение для вероятности безошибочного функционирования программного комплекса с учетом задействования всех возможных маршрутов вычислений.

Обратная задача. Определим минимальное время отладки программного комплекса при заданной вероятности его безошибочного функционирования P_зад. Процесс отладки i-го модуля обычно определяется его временем отладки t_i. В известных аналитических и эмпирических моделях оценивания надежности программ параметр t_i, как и параметр t_i - заданное время работы i-го модуля, входит в соответствующее выражение для показателя надежности модуля. При этом предполагается, что оценки искомых показателей являются известными выражениями, определяемыми по результатам испытаний. Подобных моделей известно несколько. В качестве удобного примера, не нарушающего общности подхода, приведем одну из самых ранних моделей – модель Мусы [7].

Согласно этой модели, вероятность безошибочной работы i-го модуля программного комплекса выражается формулой:

P_i(t_i,t_i) = exp[-l_it_iexp(-n_it_i)], (8.3)

где l_i и n_i – интенсивности проявления ошибки и устранения ее при отладке программы модуля; t_i и t_i – времена вычислений и отладки модуля.

Обычно используют l_i = 1/T_i, где T_i – начальное среднее время безошибочной работы модуля ;n_i = K_i / (N_ошiT_i), K_i – коэффициент сжатия времени отладки (тестирования) по сравнению с временем вычислений, N_ошi - предполагаемое первоначальное число ошибок в модуле.

Найдем минимальное время отладки программного комплекса как 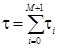, при котором P(t,t) ³ P_зад, предполагая, что справедливо (8.3). Решение получим, используя метод неопределенных множителей Лагранжа [13]. Функция Лагранжа имеет вид:

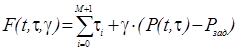, (8.4)

где g - множитель Лагранжа.

Дифференцируя (18) по аргументам t_i и g и приравнивая полученные выражения к нулю, получим систему уравнений:

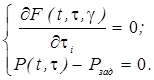(8.5)

Решив (8.5) относительно 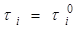получим: .

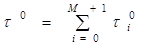Если необходимо определить максимальное значение вероятности безошибочного функционирования программного комплекса при заданном времени его отладки, то необходимо составить функцию Лагранжа в виде

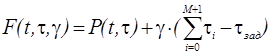. (8.6)

Дифференцируя (8.6) по t_i и g , приравнивая результаты к нулю, получим систему уравнений:

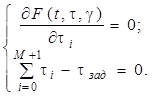(8.7)

Решая (8.7), находим искомые значения t_i, подставляя затем их в выражение для P(t,t), найдем максимальное значение вероятности безошибочного функционирования программного комплекса.

Пример.

1. Пусть требуется найти значение вероятности безошибочного функционирования программного комплекса, стохастический граф которого приведен на рис.2.

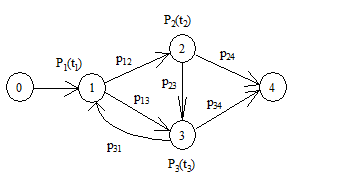
Рисунок 2 – Стохастический граф функционирования программного комплекса

Известны K_i=1, t₁=1 c, t₂ =7 c, t₃=10 c, N_ош1=10, N_ош2=5, N_ош3=3, 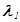=0,01 1/c, 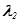=0,02 1/c, 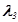=0,03 1/c, p₁₂=0,7, p₁₃=0,3, p₂₃=0,6, p₂₄=0,4, p₃₁=0,8, p₃₄=0,2. P_i(t_i,i) оцениваются формулой (17), а М=3. Матрицы G и I-G равны:

G = ;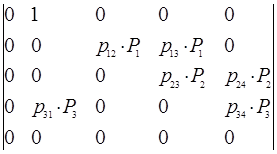

(I - G) = .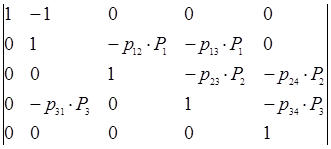

Элементы матрицы (I-G) с номером (0,4) по (16) Y = Q / R, где Q – алгебраическое дополнение элемента (4,0) матрицы (I-G), а R - главный определитель матрицы (I-G). Раскрывая данные определители, получим:

Y = P(t, 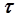)= 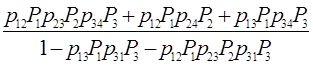. (8.8)

В формуле (8.8) аргументы t_i и t_i для краткости опущены. Подставляя исходные данные в эту формулу, положив t_i=0, будем иметь P(t,0)=0,563.

2. Пусть задано значение вероятности для программного комплекса P_зад ³ 0,999. Требуется найти времена отладок каждого модуля и суммарное минимальное время отладки комплекса. Поступая, как описано в п. ”Обратная задача”, находим:

t₁= 3460 с ; t₂= 1871 с ; t₃= 848с ; t= 6179 с.

3. Пусть задано время отладки программного комплекса t_зад=6000 с. Требуется найти времена отладок каждого модуля t_i и максимальное значение вероятности его безошибочного функционирования при тех же значениях параметров п.1 “Пример”. Получим:

t₁= 3327с ; t₂= 1838с ; t₃= 835с ; maxP(t,t)=0,999.

Приведенный числовой пример иллюстрирует возможность использования рассмотренных матричных моделей для решения прикладных задач, связанных с анализом надежности программных комплексов и обеспечением требуемых значений показателей их надежности при отладке.

Разработчики программ и лица, выполняющие отладку вновь создаваемых программных комплексов, могут получать временные оценки для выбора оптимальных величин времени отладки программных модулей и комплексов программ в целом. При решении задач обеспечения заданной надежности программного комплекса нетрудно учесть с помощью коэффициентов K_i квалификацию разработчиков программ конкретных программных модулей.

В приведенном методе могут использоваться любые модели роста надежности, получаемые теоретически или на основе экспериментальных данных.