Теоретические сведения к практической работе. Тема: Комплексные числа и действия с ними.
Тема: Комплексные числа и действия с ними.
Цель: сформировать умение выполнять арифметические действия с комплексными числами.
Теоретические сведения к практической работе
Комплексное число – это выражение вида
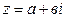 , (1.1)
, (1.1)
где а, в – действительные числа, а 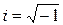 – мнимая единица.
– мнимая единица.
Первое из действительных чисел, а, называется действительной частью комплексного числа; второе, в, - мнимой частью.
Выражение (1.1) называют алгебраической формой записи комплексного числа.
Числом, сопряженным к 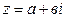 , называют число вида
, называют число вида 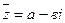 . Используя формулу разности квадратов, получаем, что
. Используя формулу разности квадратов, получаем, что 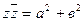 . Можно доказать, что корнями квадратного уравнения с отрицательным дискриминантом являются два сопряженных комплексных числа.
. Можно доказать, что корнями квадратного уравнения с отрицательным дискриминантом являются два сопряженных комплексных числа.
Пример 1. Решить уравнение 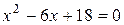 .
.
Решение. Дискриминант данного уравнения: 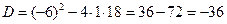 меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
меньше нуля, но теперь мы можем воспользоваться мнимой единицей:
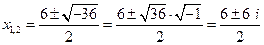 , т.е.
, т.е. 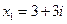 ;
; 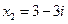 .
.
Справедливы следующие правила арифметических действий над комплексными числами 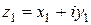 и
и 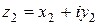 :
:
1) 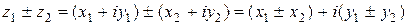 (осуществляется сложение или вычитание алгебраических двучленов и приведение подобных);
(осуществляется сложение или вычитание алгебраических двучленов и приведение подобных);
2) 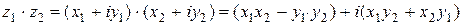 (осуществляется перемножение алгебраических двучленов и приведение подобных с учетом того, что
(осуществляется перемножение алгебраических двучленов и приведение подобных с учетом того, что 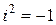 );
);
3) 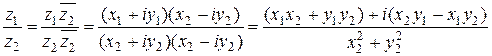 (эта операция возможна только в случае, когда
(эта операция возможна только в случае, когда 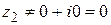 ).
).
Пример 2. Вычислить 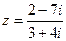 и указать вещественную и мнимую части полученного комплексного числа.
и указать вещественную и мнимую части полученного комплексного числа.
Решение. Действуя в соответствии с правилами получаем:
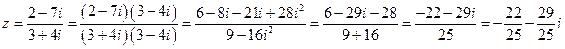 ;
;
поэтому 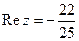 ,
, 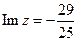 .
.
Тригонометрическая форма комплексного числа.
Каждому комплексному числу вида (1.1) можно поставить в соответствие точку M(x;y) на декартовой плоскости (при этом на оси OX располагаются вещественные числа 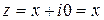 , а на оси OY – чисто мнимые числа
, а на оси OY – чисто мнимые числа 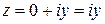 ).
).
Модулем комплексного числа назовем длину отрезка 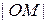 (или расстояние от начала координат до точки M), т.е.
(или расстояние от начала координат до точки M), т.е. 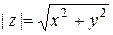 . Аргументом комплексного числа (
. Аргументом комплексного числа ( 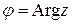 ) назовем угол, который вектор
) назовем угол, который вектор 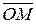 образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию
образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию 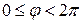 . При этом выражение вида
. При этом выражение вида
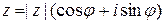 (1.2)
(1.2)
называется тригонометрической формой записи комплексного числа.
Преобразуем (1.1)
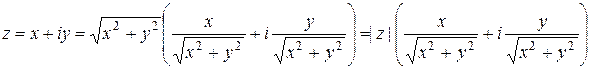
и, сравнивая с (1.2), получаем, что аргумент z можно найти, решив систему
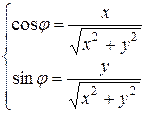 или
или 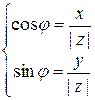 (1.3.)
(1.3.)
Пример 3. Записать комплексное число в тригонометрической форме 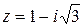 , указать модуль и аргумент комплексного числа.
, указать модуль и аргумент комплексного числа.
Решение. По определению 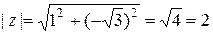 . Для определения аргумента воспользуемся формулой:
. Для определения аргумента воспользуемся формулой: 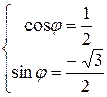 . Получаем, что
. Получаем, что 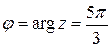 . Тригонометрическая форма заданного комплексного числа имеет вид:
. Тригонометрическая форма заданного комплексного числа имеет вид: 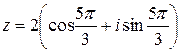 .
.
Возведение в степень и извлечение корней. Если комплексное число задано тригонометрической формой 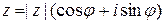 , то справедлива формула Муавра
, то справедлива формула Муавра
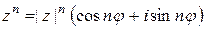 . (1.4)
. (1.4)
Для извлечения корня n-й степени (n – целое число, большее 1) из комплексного числа, заданного в тригонометрической форме, применяется формула, дающая n значений этого корня:
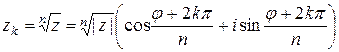 , k=0,1,…,n-1. (1.5)
, k=0,1,…,n-1. (1.5)
Пример 4. Вычислить: a) 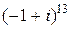 ; b)
; b) 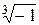 .
.
Решение. В задании a), чтобы воспользоваться формулой Муавра, необходимо представить комплексное число в тригонометрической форме. Имеем: 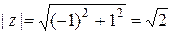 ;
; 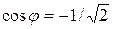 и
и 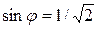 , т.е.
, т.е. 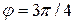 (так как соответствующая точка лежит во второй четверти). Следовательно,
(так как соответствующая точка лежит во второй четверти). Следовательно, 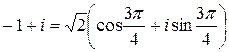 и
и 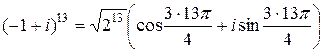 (в силу (1.4)). Учитывая что
(в силу (1.4)). Учитывая что 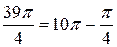 и используя свойства тригонометрических функций, получаем:
и используя свойства тригонометрических функций, получаем:
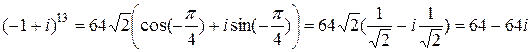 .
.
В задании b) тригонометрическая форма заданного числа имеет вид 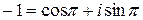 (|z|=1), поэтому в силу (1.5)
(|z|=1), поэтому в силу (1.5)
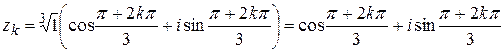 , k=0,1,2.
, k=0,1,2.
Выписываем три искомых корня:
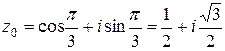 ;
;
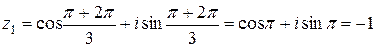 ;
;
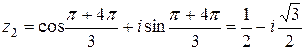 .
.
Содержание практической работы
Задание 1. Вычислить, выписать действительную и мнимую части полученных комплексных чисел.
1) 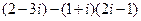 2)
2) 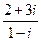 3)
3) 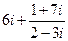
4) 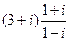 5)
5) 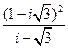 6)
6) 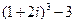
7) 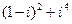
Задание 2. Запишите предложенные комплексные числа в тригонометрической форме: 1) 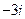 ; 2)
; 2) 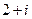 ; 3)
; 3) 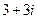 ; 4)
; 4) 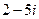 5)
5) 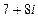 6)
6) 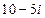 7)
7) 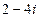 .
.
Задание 3. Найти все корни уравнений:
1) 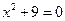 ; 2)
; 2) 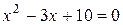 ; 4)
; 4) 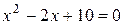 ; 5)
; 5) 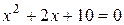 ; 6)
; 6) 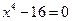 7)
7) 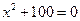
Контрольные вопросы:
1. Что такое комплексное число?
2. Что такое алгебраическая форма записи комплексного числа?
3. Перечислите правила сложения, вычитания, умножения комплексных чисел
4. Как выполнить деление комплексных чисел?
5. Как найти корни квадратного уравнения с отрицательным дискрименантом?
