Теоретико-множественные операции над отношениями в реляционной модели данных

Обработку данных реляционной модели можно реализовать методами реляционной алгебры.

Реляционная алгебра, определена Коддом и содержит 8 операций, разделенных на две группы:

1. Теоретико – множественные операции - объединение, пересечение, вычитание и декартово произведение.

2. Специальные реляционные операции – выборка, проекция, соединение, деление

Теоретико-множественные операции

Реляционный оператор представляет собой функцию с отношениями в качестве аргументов и возвращающую отношение в качестве результата.

R=f(R1, R2….. Rn)

В качестве аргументов в реляционные операторы могут быть проставлены другие реляционные операторы, подходящие по типу.

R=f(f1(R11, R21….. Rn1), f2(R21, R22….. R2n)….)

В силу этого реляционная алгебра является замкнутой.

Отношения называются совместимыми по типу, если они имеют идентичные заголовки, а именно:

1. отношения имеют одно и тоже множество имен атрибутов, т.е. для любого атрибута в одном отношении найдется атрибут с таким же наименованием в другом отношении.

2. атрибуты с одинаковыми именами определены на одних и тех же доменах.

Некоторые отношения не являются совместимыми по типу, но становятся таковыми после переименования атрибутов.

Оператор переименования R rename A1,A2,… as new A1, new A2…,

Например:

R rename student as starosta

Объединение

Объединением двух совместимых по типу отношений называется отношение с тем же заголовком, что и у R1 и R2, и телом, включающим все кортежи операндов, за исключением повторяющихся.

Синтаксис R1 union R2

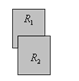
R1

Шифр	Фамилия	Стипендия
	Котова
	Серов
	Леонидов

R2

Шифр	Фамилия	Стипендия
	Котова
	Даниленко
	Леонидов

Объединение

Шифр	Фамилия	Стипендия
	Котова
	Серов
	Леонидов
	Даниленко
	Леонидов

Операторы не передают результату никаких данных о потенциальных ключах.

Пересечение

Пересечением двух совместимых по типу отношений R1 и R2 называется отношение с тем же заголовком, что и у отношений R1 и R2, и телом, состоящим из кортежей, принадлежащих одновременно обоим отношениям R1 и R2.

Синтаксис

R1 intersect R2

Шифр	Фамилия	Стипендия
	Котова

Вычитание

Вычитанием двух совместимых по типу отношений R1 и R2, называется отношение с тем же заголовком, что и у отношений R1 и R2, и телом, состоящим из кортежей, принадлежащих отношению R1 и не принадлежащих R2.

Синтаксис R1 minus R2

Шифр	Фамилия	Стипендия
	Серов
	Леонидов

Декартово произведение

Декартовым произведением двух отношений R1(R11, R12, R13…) и R2(R21,R22,R23,…) называется отношение, заголовок которого является сцеплением заголовком отношений R1 и R2:

(R11, R12, R13… R21,R22,R23,…), а тело состоит из кортежей, являющихся сцеплением кортежей отношений R1 и R2

(r11, r12, r13… r21, r22, r23….), таких что (r11, r12, r13…) принадлежит R1, а (r21, r22, r23….) принадлежит R2/

Синтаксис R1 times R2

Мощность произведения равна произведению мощностей. Если атрибуты R1 и R2 имеют атрибуты с одинаковыми наименованиями, то перед выполнением операции декартового произведения такие атрибуты необходимо переименовать. Совместимость по типу не требуется.

R1

Шифр	Фамилия
	Котова
	Серов
	Леонидов

R2

Код	Название
	Математика
	Философия

R1 times R2

Шифр	Фамилия	Код	Название
	Котова		Математика
	Котова		Философия
	Серов		Математика
	Серов		Философия
	Леонидов		Математика
	Леонидов		Философия

Специальные реляционные операторы

Выборка (ограничение, селекция)

Выборку называют горизонтальным срезом отношения по некоторому условию.

Выборкой на отношении R с условием С называется отношение с тем же заголовком, что и у отношения R, и телом, состоящим из кортежей, значения атрибутов которых при подстановке в условие С дают значение ИСТИНА.

Обычно условие С имеет вид R11Q R12, где Q принадлежит {=<>¹³£}, а R11 и R12 атрибуты отношения R или скалярные значения. Такие выборки называются Q - выборки.

Синтаксис R where C или R where R11Q R12

Шифр	Фамилия	Стипендия
	Котова
	Серов
	Леонидов

Выборка R where стипендия >250

Шифр	Фамилия	Стипендия
	Котова
	Леонидов

Проекция

Проекцией отношения R по атрибутам R1, R2, R3…Rn, где каждый атрибут принадлежит R, называется отношение с заголовком (R1, R2, R3…Rn) и телом, содержащим множество кортежей вида (r1,r2,r3,…rn). При этом дубликаты кортежи удаляются.

Проекцию называют вертикальным срезом отношения.

Синтаксис R[R1, R2, R3…Rn]

Шифр	Фамилия	Факультет
	Котова	ФИРЭ
	Серов	Энергетический
	Леонидов	ФИРЭ
	Серов	СФ

R[факультет]

Факультет

ФИРЭ

Энергетический

ФИРЭ

СФ

Соединение

Обычно рассматривают несколько разновидностей операции соединения.

Общая операция соединения

Q-соединение

Экви-соединение

Естественное соединение

Наиболее важным из этих операций является операция естественного соединения. Так как остальные разновидности соединения являются частными случаями общей операции соединения.

Общая операция соединения:

Соединением отношений R1 и R2 по условию называется отношение

(R1 times R2) where C, где С представляет собой логическое выражение, в которое могут входить атрибуты отношений R1 и R2 и/или скалярные выражения. То есть, чтобы выполнить операцию соединения, необходимо выполнить последовательно операцию декартова произведения и выборки. Если в отношениях R1 и R2 имеются атрибуты с одинаковыми наименованиями, то перед выполнением соединения такие атрибуты необходимо переименовать.

Q-соединение

(R1 times R2) where R11QR21 - Q-соединение отношения R1 по атрибуту R11 с отношением R2 по атрибуту R21. Записывают и

R1 [R11QR21] R2

R1

Шифр	Фамилия	Курс
	Котова
	Серов
	Леонидов

R2

Код	Наименование	Семестр
	Математика
	Ин яз
	Философия
	ИОСУ
	Сложные системы

Какие экзамены должны быть сданы студентами, закончившими учебный год R1[семестр <=2*курс]R2

Шифр	Фамилия	Курс	Код	Наименование	Семестр
	Котова			Математика
	Котова			Ин яз
	Котова			Философия
	Серов			Философия
	Серов			Математика
	Леонидов			Математика
	Леонидов			Ин яз
	Леонидов			Философия

Экви соединение это соединение, когда Q есть равенство.

Естественное соединение

Пусть даны отношения R1(R11,R12,R13,..R1n,Z1,Z2,…Zn) и R2(Z1,Z2,…Zn, R21,R22,R23,..,R2m). Тогда естественным соединением отношений R1 и R2 называется отношение с заголовком (R11,R12,R13,..R1n,Z1,Z2,…Zn, R21,R22,R23,..,R2m) и телом, содержащим множество кортежей (r11,r12,r13,…r1n,z1,z2,z3,…zn, r21, r22,…r2m), таких что (r11,r12,r13,…r1n,z1,z2,z3,…zn) принадлежит R1, а (z1,z2,z3,…zn, r21, r22,…r2m) принадлежит R2

Синтаксис

R1 join R2

Соединение производится по одинаковым атрибутам.

R1

Шифр	Фамилия
	Котова
	Серов
	Леонидов

R2

Код	Наименование
	Математика
	Ин яз
	Философия

R3

Шифр	Код	Оценка

R1 join R2 join R3

Шифр	Фамилия	Код	Наименование	оценка
	Котова		Математика
	Котова		Ин яз
	Котова		Философия
	Серов		Математика
	Серов		Философия
	Леонидов		Ин яз

Деление

У операции деления два операнда бинарное и унарное. Результативное отношение состоит из одноатрибутивных кортежей, включающих значения первого атрибута кортежей первого операнда-отношения, таких что множество значений второго атрибута совпадает со множеством значений единственного атрибута второго операнда-отношения.

Синтаксис R1 divideby R2

R1

Шифр	Код

R2

Код

R1 divideby R2

Шифр

Для работы с БД, которые частично или полностью используют реляционную модель данных предназначен язык SQL. Язык разработан на основе реляционной алгебры и относится к непроцедурным языкам программирования (можно определить то, что необходимо выполнить, а не то как это сделать). Язык оперирует отношениями и в результате инструкций языка получается отношение.

Первый стандарт языка разработан в 1989 году Национальным институтом стандартизации США (ANSI). В 1992 году появилась версия SQL92, в 1999 году SQL3. Сегодня различают различные типы диалектов, расширяющие стандарт языка.

Существуют две формы языка:

Интерактивный - создание запросов в режиме диалога

Встроенный - инструкции языка, которые встраиваются внутрь программ, написанных на другом языке (например, при разработке приложений, обрабатывающих данные, расположенные в БД).

Рассмотрим интерактивную форму.

Типы команд языка

DDl- язык определения данных

CREATE TABLE, ALTER TABLE, DROP TABLE, CREATE VIEW, ALTER VIEW, DROP VIEW, CREATE INDEX, DROP INDEX

DML – язык манипулирования данными

INSERT, UPDATE, DELETE

DQL – язык запросов к данным

SELECT

DCL – язык управления данными, либо команды администрирования данных

CREATE DATABASE, ALTER DATABASE, DROP DATABASE, GRANT (предоставление прав доступа для действий над заданными объектами БД), REVOKE (лишение прав доступа для действий над заданными объектами БД) и др.

Команды администрирования данных- предоставляют возможность аудита и анализа операций внутри БД. Могут использоваться при анализе производительности системы данных в целом.

START AUDIT, STOP AUDIT

Команды управления транзакциями – позволяют выполнить обработку информации, объединенной в транзакцию

COMMIT, ROLLBACK, SAVE POINT, SET TRANSACTION (назначение имени транзакции)

Процедурный язык

DECLARE, OPEN, FETCH, CLOSE, EXECUTE и др.

25. Устойчивость линейных непрерывных систем. Критерий устойчивости Найквиста.

Устойчивость линейных САУ. Если какое-либо решение линей­ного дифференциального уравнения с постоянными коэффициентами асимптотически устойчиво, то асимптотически устойчиво любое его решение. Поэтому в случае непрерывных линейных стацио­нарных систем, т. е. систем, описываемых линейными дифференциальными уравнениями с постоянными коэффициентами, можно рассматривать их устойчивость, не указывая конкретного движения.

Непрерывная линейная стационарная САУ называется устой­чивой, если асимптотически устойчиво какое-либо ее невозмущенное (заданное) движение.

Если заданы внешние воздействия, то уравнение линейных стационарных САУ можно представить в виде

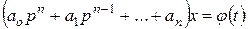(5.6)

В уравнении (5.6) a_i, i=0, 1, ..., п — заданные постоянные коэффициенты, 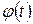— заданная функция времени.

Общее решение уравнения (5.6), как известно, имеет вид

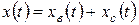(5.7)

где 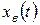— частное решение неоднородного уравнения (5.6), 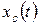— общее решение однородного уравнения

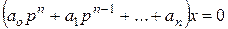(5.8)

Частное решение х_в(t)определяет вынужденное движение, реше­ние 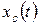— свободное движение, т. е. движение, которое не зависит от внешних воздействий и определяется только начальными усло­виями.

Невозмущенное движение задается внешним задающим воздействием и при отсутствии внешних возмущаю­щих воздействий совпадает с вынуж­денным движением 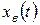. Поэтому линейная система устойчива, когда

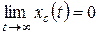(5.9)

Это соотношение можно принять за определение устойчивости линейных непрерывных систем.

Критерий устойчивости Найквиста позволяет исследовать устойчивость замкнутых систем по АФХ разомкнутой системы. Разомкнутая система может быть неустойчивой, устойчивой, нейтральной (на границе устойчивости).

Если разомкнутая САР неустойчива, то среди корней ее характеристического уравнения А(р)=0 есть m – правых корней и n-m – левых корней. Тогда согласно принципу аргумента получим

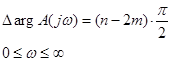
Чтобы замкнутая САР была устойчивой, надо чтобы ее характеристическое уравнение имело бы все корни левые (А(р) +В(р)=0; Р_i 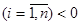- все корни левые). Тогда

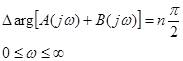
В этом случае, согласно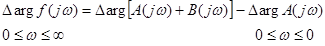

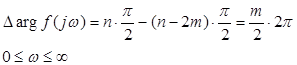
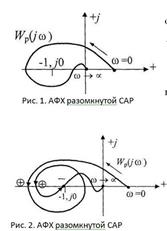Множитель 2π обозначает, что вектор f(jω) совершает вокруг начала координат полный оборот. Тогда критерий Найквиста для неостойчивых разомкнутых систем может быть сформулирован следующим образом:

Для устойчивости замкнутой САР при неустойчивой разомкнутой системе необходимо и достаточно, чтобы АФХ разомкнутой CAP W_р(jω), начинаясь на положительном отрезке положительной оси (действительной оси), при росте частоты ω от 0 до ∞ охватывала точку
(-1,j0) в положительном направлении 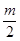раз, где т -число правых корней характеристического уравнения разомкнутой САР.

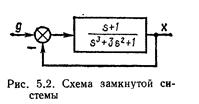
Пусть Wp(jω) имеет вид, изображенный на рисунке 1, охватывает точку (-1,j0) в положительном направлении 1 раз, т.е. 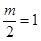, поэтому m= 2.

При такой АФХ если разомкнутая система имеет 2 правых корня, то замкнутая система устойчива. Часто из-за наличия местных обратных связей АФХ разомкнутой САР совершает несколько оборотов вокруг точки (-1, j0) и имеет достаточно замкнутую конфигурацию (рис. 2) Здесь подсчитывать число оборотов W_p(jω) вокруг точки
(-1, j0) затруднительно. Для подобных случаев видный советский ученый Я. 3. Цыпкин предложил удобную методику, базирующуюся на понятиях положительного и отрицательного переходов.

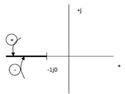Переход амплитудно-фазовой характеристикой разомкнутой CAP W_p(jω) сростом частоты отрезка действительной оси (-;-1j0] сверху вниз называется положительным (+), а снизу в верх - отрицательным (-).

Тогда критерий Найквиста в формулировке Цыпкина предстает в следующем виде: Замкнутая САР устойчива, если разность между числом положительных и отрицательных переходов равна 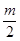, где т - число правых корней характеристического уравнения разомкнутой системы.

На рис. 2 изображен случай, когда имеется два положительных и один отрицательный переход,
т.е. 2(+) – 1(-) = 1 = 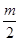, и, значит, если характеристическое уравнение разомкнутой САР имеет 2 правых корня (только в этом случае!), то замкнутая САР устойчива. Подчеркнем еще раз, что при подсчете переходов исследуется только тот участок (-∞;-1j0] и не принимается во внимание остальная часть действительной оси.

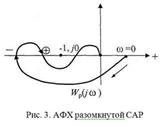
Рассмотрим случай 2 для неустойчивой разомкнутой САР (рис. 3) .

На этом рисунке изображена АФХ разомкнутой системы, имеющая 1 положительный и 1 отрицательный переходы. По Цыпкину: 1(+) - 1(-) = 0 = 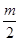. Таким образом, система будет устойчива, если разомкнутая система тоже устойчива, т.е. имеет т=0 правых корней своего характеристического уравнения.

Другой вариант ответа

Если разомкнутая САР неустойчива, то среди корней ее характеристического уравнения 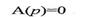есть т правых корней. Тогда согласно принципу аргумента получим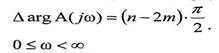

Чтобы замкнутая САР была устойчивой, надо чтобы ее характеристическое уравнение имело бы все корни левые, следовательно, согласно принципу аргумента:

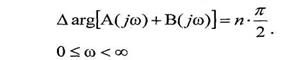Тогда в этом случае согласно (IV. 3.7) получим (изменение аргумента вспомогательного вектора)

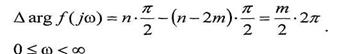
Множитель 2л обозначает, что вектор f(jω) совершает вокруг начала координат полный оборот.

Тогда критерий Найквиста для неустойчивых разомкнутых систем при учете (IV.3. 9) может быть сформулирован следующим образом:

Для устойчивости замкнутой САР при неустойчивой разомкнутой системе необходимо и достаточно, чтобы АФХ разомкнутой CAP W_p(jω), начинаясь на действительной оси, при росте частоты ω от 0 до ∞ охватывала точку (-1, j0) в положительном направлении т/2 раз, где т -число правых корней характеристического уравнения разомкнутой САР.

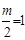Пусть W_p(jω) имеет вид, изображенный на рис. IV.1.6, охватывает точку (-1,j0) в положительном направлении 1 раз, т.е. , поэтому m=2.

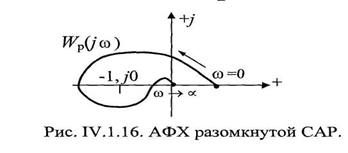Если характеристическое уравнение разомкнутой САР имеет 2 правых корня, система в замкнутом состоянии устойчива. Для W_p(jω), изображенной на рис. IV.16, наличие у характеристического уравнения разомкнутой системы числа правых корней не равных 2, означает неустойчивость замкнутой САР.

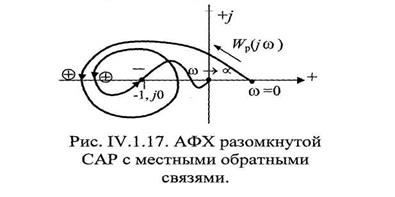Часто из-за наличия местных обратных связей АФХ разомкнутой САР совершает несколько оборотов вокруг точки (-1,j0) и имеет достаточно замкнутую конфигурацию (рис. IV.17).

Здесь подсчитывать число оборотов W_p(jω) вокруг точки (-1, j0) затруднительно. Для подобных случаев видный советский ученый Я. 3. Цыпкин предложил удобную методику, базирующуюся на понятиях положительного и отрицательного переходов.

Переход амплитудно-фазовой характеристикой разомкнутой CAP W_p(jω) ростом частоты отрезка действительной оси (-∞;-1] сверху вниз называется

положительным (+), а снизу в верх - отрицательным (-).

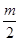Тогда критерий Найквиста в формулировке Цыпкина предстает в следующем виде: Замкнутая САР устойчива, если разность между числом положительных и отрицательных переходов равна , где т - число правых корней характеристического уравнения разомкнутой системы.

На рис. IV.17 изображен случай, когда имеется два положительных и один отрицательный переход, т.е.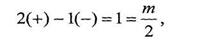

и, значит, если характеристическое уравнение разомкнутой САР имеет 2 правых корня (только в этом случае!), то замкнутая САР устойчива. Подчеркнем еще раз, что при подсчете переходов исследуется только тот участок (-∞;-1] и не принимается во внимание остальная часть действительной оси.

Сейчас мы рассмотрим случай IV. 3. 3. 2 для неустойчивой разомкнутой САР. Однако, вышеприведенная формулировка Цыпкина критерия Найквиста применима к случаю IV.3. 3. 1, т. е. для устойчивой разомкнутой САР (рис. IV. 18).

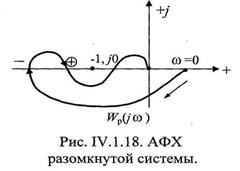На рисунке изображена АФХ разомкнутой системы, имеющая 1 положительный и 1 отрицательный переходы. По Цыпкину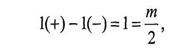

таким образом, система будет устойчива, если разомкнутая система тоже устойчива, т.е. имеет т=0 правых корней своего характеристического уравнения, а это и есть случай IV. 3.3.1.

Идентификация статических объектов. Планирование эксперимента. Полный факторный эксперимент.

Планирование эксперимента

Большинство научных исследований связано с экспериментом. Он проводится в лабораториях, на производстве, на опытных полях и т.д. Эксперимент может быть физическим, психологическим или модельным. Он может проводиться как на самом объекте так и на модели. Модель, как известно, может отличаться от реального объекта масштабом, а иногда природой (пример).

Так что же такое эксперимент? Под экспериментом будем понимать совокупность действий, к которым приходится обращаться, чтобы задавать объекту управления интересующие нас вопросы. Эта совокупность может быть очень сложной, но её всегда можно разложить на отдельные элементы, каждый из которых называется опытом. Существуют и другие определения эксперимента. Одним из возможных путей повышения эффективности исследований является применение математических методов - построение математической теории планирования эксперимента.

Планирование эксперимента - это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленных задач с требуемой точностью.

При этом существенно следующее:

1) стремление к минимизации общего числа опытов;

2) одновременное варьирование всеми переменными, определяющими
процесс, по специальным правилам - алгоритмам;

3) использование математического аппарата, формализующего многие
действия эксперимента;

4) выбор чёткой стратегии, позволяющей принимать обоснованные
решения после каждой серии экспериментов.

Задачи, для решения которых может использоваться планирование эксперимента (ПЭ), чрезвычайно разнообразны:

1) поиск оптимальных условий;

2) построение интерполяционных формул;

выбор существенных факторов;

3) уточнение констант теоретических моделей.

Задачи поиска оптимальных условий являются одними из наиболее распространенных научно-технических задач. Они возникают в тот момент, когда установлена возможность проведения процесса и необходимо найти наилучшие условия его реализации.

Задачи, сформулированные таким образом, называются задачами оптимизации. Процесс их решения называется процессом оптимизации или просто оптимизацией. Выбор оптимального состава многокомпонентных смесей или сплавов, повышение производительности действующих установок, повышение качества продукции, снижение затрат на её получение - все это примеры задач оптимизации. Эксперимент, который ставится для решения задачи оптимизации - называется экстремальным.

Примеры.

Для описания объекта исследования удобно воспользоваться понятием «черного ящика»:

Черный ящик

Входы: Выходы:

X₁ Y₁

X₂ Y₂

X_n Уm

		целевая функция
	Факторы

Рис.1

Каждый из факторов может принимать в опыте одно из нескольких значений. Такие значения будем называть уровнями. Каждый фактор имеет определенное число дискретных уравнений. Фиксированный набор уровней факторов определяет одно из возможных состояний черного ящика. Если перебрать все возможные выборы состояний, то получим полное множество различных состояний данного ящика (объекта исследований). Одновременно это будет число возможных различных опытов. Чтобы узнать число различных состояний, достаточно число уровней факторов возвести в степень числа факторов 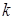: 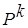, где р - число уравнений.

Планирование эксперимента предполагает активное вмешательство в процесс и возможность выбора в каждом опыте тех уровней факторов, которые представляют интерес. Поэтому такой эксперимент называется активным. Объект, на котором возможен активный эксперимент, называется управляемым.

На практике нет абсолютно управляемых объектов. На реальный объект обычно действуют как управляемые, так и неуправляемые факторы. Неуправляемые факторы влияют на воспроизводимость эксперимента и являются причиной её нарушения. Если требования воспроизводимости не выполняются, приходится обращаться к активно-пассивному эксперименту.

Планирование эксперимента - это метод выбора количества и условий проведения опытов, минимально необходимых для отыскания оптимальных условий, т.е. для решения поставленной задачи.

Результаты эксперимента используются для получения математической модели объекта исследований, которая представляет собой уравнение, связывающее, например, оптимизации и факторы. Такое уравнение называют функцией отклика.

Параметр оптимизации

При планировании экстремального эксперимента очень важно определить параметр, который нужно оптимизировать. Сделать это совсем не просто, как кажется на первый взгляд. Цель исследования должна быть сформулирована очень четко и допускать количественную оценку. В зависимости от объекта и цели исследования параметры оптимизации могут быть очень разнообразными.

Введем некоторую классификацию параметров оптимизации рис.2. Параметр оптимизации - это признак, по которому оптимизируется процесс. Он должен быть количественным, задаваться числом. Его необходимо уметь измерять при любой возможной комбинации выбранных уровней факторов. Множество значений, которые может принимать П.О., будем называть областью его определения. Области определения могут быть непрерывными и дискретными, ограниченными и неограниченными. Например, выход реакции - это параметр оптимизации с непрерывной ограниченной областью определения. Он может изменяться в интервале от 0 до 100%. Число бракованных изделий, число зерен на шлифе сплава, число кровяных телец в пробе крови - это примеры параметров с дискретной областью определения, ограниченной снизу.

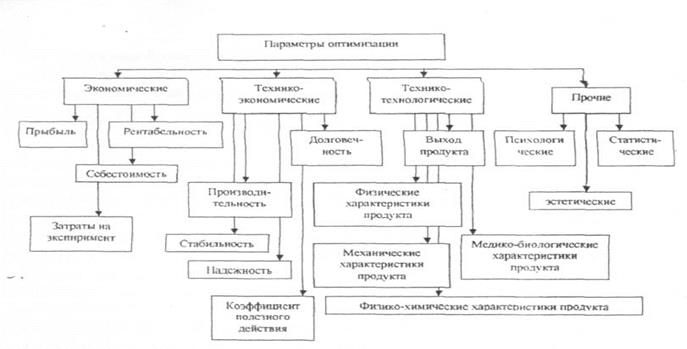
Рис.2 Классификация параметров оптимизации

Уметь измерять параметр оптимизации - это значит располагать подходящим прибором. В некоторых случаях такого прибора может не существовать либо он слишком дорог. Если нет способа количественного измерения результата, то приходится воспользоваться приемом, называем ранжированием (ранговым подходом). При этом П.О. присваиваются оценки - ранги по заранее выбранной шкале: 2^х бальной, 5^й бальной и т.д. ранговый П.О. имеет дискретную ограниченную область определения. Ранг - это количественная оценка П.о., но она носит условный (субъективный) характер. П.О. должен быть:

1) эффективным с точки зрения достижения цели;

2) универсальным;

3) количественным и выражаться одним числом;

4) статически эффективным (точные измерения);

5) имеющим физический смысл, простым и легко вычисляемым;

6) однозначным.

Факторы

После того как выбран объект исследования и П.О., нужно включить в рассмотрение все существующие факторы, которые влияют на процесс. Если какой-либо существующий фактор не учтен, то это может привести к неприятным последствиям. Чем больше факторов, то тем больше опытов необходимо провести, так как 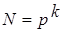. Если число факторов больше 15, нужно обратиться к методам отсеивания несущественных факторов.

Выводы:

1. Факторы - это величины, соответствующие способам воздействия внешней среды на объект. Они определяют как сам объект, так и его состояние. Требования к факторам: управляемость и однозначность. Управлять фактором - это значит установить нужное значение и поддерживать его постоянно в течение опыта или менять по заданной программе. В этом состоит особенность активного эксперимента.
2. Планировать эксперимент можно только в том случае, если уровни факторов подчиняются воле экспериментатора.
3. Факторы должны непосредственно воздействовать на объект исследования. Трудно управлять фактором, если он является функцией других переменных, но в планировании эксперимента могут участвовать сложные факторы, такие, как логарифмы, соотношения и т.д. Факторы должны быть определены операционально.
4. Требования к совокупности факторов: совместимость и отсутствие
   линейной корреляции. Выбранное множество факторов должно был
   достаточно полным. Если какой-то существенный фактор пропущен - это приводит к неправильному определению оптимальных условий или к большой ошибке опыта. Ф. могут быть количественными и качественными.
5. Точность фиксации Ф. должна быть высокая, степень точности определяется диапазоном изменения факторов.

Выбор модели

Модели бывают разные, ихбывает много. Чтобы выбрать одну из нихнадо понять, что мы хотим от модели, какие требования к ней предъявляем. Главное требование к модели - это способность предсказывать направление дальнейших опытов, причем предсказывать с требуемой точностью. Жела­тельно, чтобы точность предсказания во всех возможных направлениях была одинакова. Это значит, что в некоторой подобласти, в которую входят и ко­ординаты выполненных опытов, предсказанные с помощью модели значения функции отклика не должно отличаться от фактического больше чем их некоторую заранее заданную величину. Модель, которая удовлетворяет такому или какому-либо аналогичному требованию, называется адекватной. Разработаны специальные статистические методы проверки адекватности модели. При выборе математической модели, при прочих равных условиях, будем предполагать степенные ряды, т.е. отрезки степенных рядов - алгебраические полиномы.

В качестве примера запишем модель в форме полинома для 2^х факто­ров. Полином нулевой степени: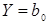

Полином первой степени: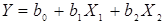

Полином второй степени: